[数据结构读书笔记 ] 队列 以及 单调队列

Posted 2022-11-22 凌星An

队列

队列的介绍

队列也是我们一种很常用的基本数据结构，符合"先进先出"的特性。即最先被放入队列的元素 ，出队时，会最先被取出。

一般来说，我们从队列右侧放入元素，可把队列右侧称为队尾 ；从队列左侧 取出元素，可把队列左侧称为 队头 。

如图所示：

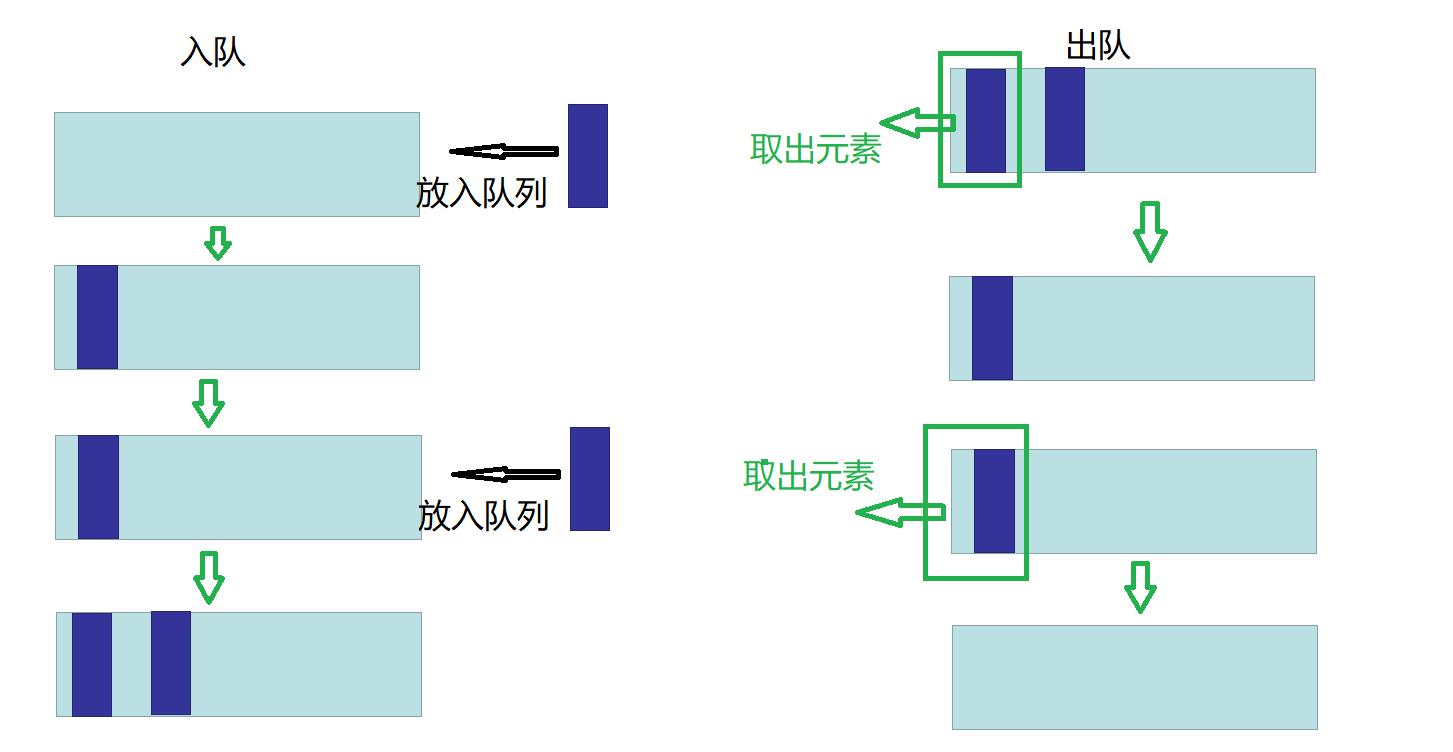
代码

const int N=100; //放入过队列中元素数量的最大值

int que[N]; //存放整形数据的队列

int hh=0,tt=-1; //hh 队头下标 tt队为下标

//判断是否为空
hh>tt  为真时，队列是空的
hh<=tt  为真时，队列时有元素的

//插入元素
que[++tt] =value

//取出元素
que[hh]  //队头元素
++hh;    //将队头元素删除掉

单调队列

单调队列的介绍

单调队列 其本质是特殊的队列， 存储的元素 具有单调性(可能单调递增也可能单调递减) 。

存储元素符合下面的规律：

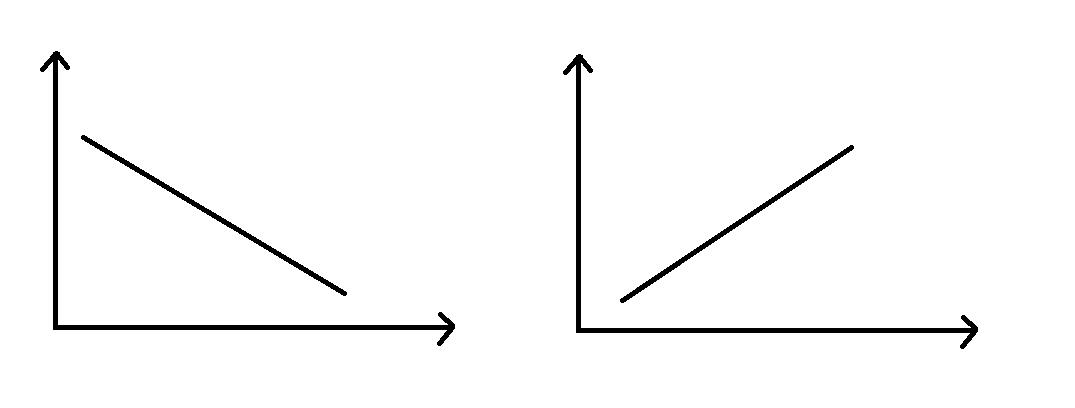
应用场景： 单调队列 大部分和 滑动窗口 可以联系起来，主要用于求取连续区间内的最大值或者最小值。

代码实现

//单调队列和队列一样，可以进行下面的操作
const int N=100; //放入过队列中元素数量的最大值

int que[N]; //队列 :存放元素下标

int hh=0,tt=-1; //hh 队头下标 tt队为下标

//判断是否为空
hh>tt  为真时，队列是空的
hh<=tt  为真时，队列时有元素的

//插入元素
que[++tt] =value


que[hh]  //获取队头元素
++hh;    //将队头元素删除掉
que[tt]  //获取队尾元素
--tt  ;  //将队尾元素删除掉

//队列求取连续区间最值问题 连续区间长度为k
   for(int i=1;i<=n;i++)  //遍历整个区间
        //如果队列不为空，判断队头是否超出范围，以当前位置为右端点，左边为k的区间
        while(hh<=tt&&que[hh]<i-k+1) ++hh;  
        //将队列中比当前元素大的，全部出队
        while(hh<=tt&& vec[que[tt]]>= vec[i])
            --tt;
        
        que[++tt]=i;
 

154. 滑动窗口
     网址: https://www.acwing.com/problem/content/156/
     

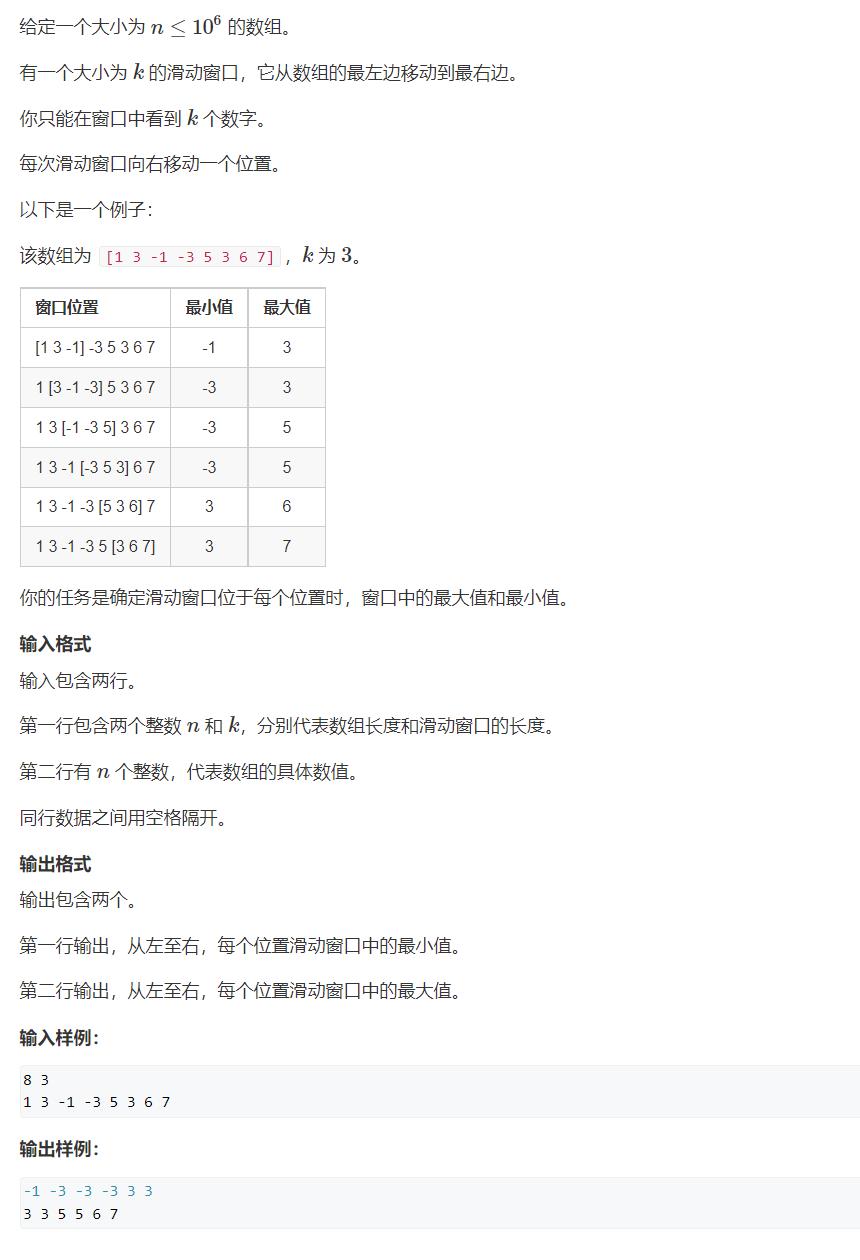
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;



const int N=1e6+10;

int vec[N];
int que[N];//存储着坐标
int hh=0,tt=-1;
int main()
    int n=0,k=0;
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)
        cin>>vec[i];
    
    for(int i=1;i<=n;i++)
        while(hh<=tt&&que[hh]<i-k+1) ++hh;
        while(hh<=tt&& vec[que[tt]]>= vec[i])
            --tt;
        
        que[++tt]=i;
        if(i>=k)
            cout<<vec[que[hh]]<<" ";
        
    
    cout<<endl;
    hh=0,tt=-1;
    for(int i=1;i<=n;i++)
        //hh<=tt 表示队列不为空
        while(hh<=tt&&que[hh]<i-k+1) ++hh;
        while(hh<=tt&& vec[que[tt]]<= vec[i])
            --tt;
        
        que[++tt]=i;
        if(i>=k)
            cout<<vec[que[hh]]<<" ";
        
    
    return 0;

参考

1. acwing.com
2. 《算法进阶指南》