(2021.9.16)针对数组和链表的时间复杂度详解
Posted Mr. Dreamer Z
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了(2021.9.16)针对数组和链表的时间复杂度详解相关的知识,希望对你有一定的参考价值。
由于工作原因,很久没有写一些学习的博客了。
最近抽空在看数据结构和时间复杂度的文章,今天想谈一下数组和链表相关的问题。
目录
1. 数组
1.1 什么是数组
数组就是由相同类型的元素集合组成的固定长度的一种数据结构。在内存中开辟的空间是顺序存储的,因此可以通过下标index计算出某个元素的地址。
需要提前预约空间。
1.2 数据结构
1.2.1 一维数组
int[] arr = 1,2,3,4;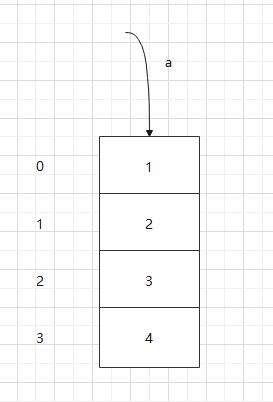
如上图所示,如果我们编写上述代码。那么可视为栈中会出现这一个数据结构。
或者我们这样:
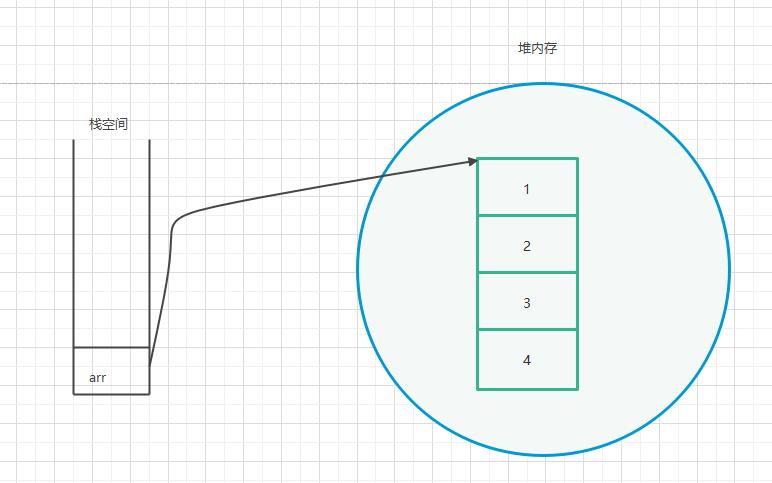
int[] arr = new int[4];
arr[0] = 1;
arr[1] = 2;
arr[2] = 3;
arr[3] = 4;由于我们使用了new关键字,所以会在堆中开辟空间
1.2.2 多维数组
int[][] arr = 1,2,3,4,5,6,7,8,9;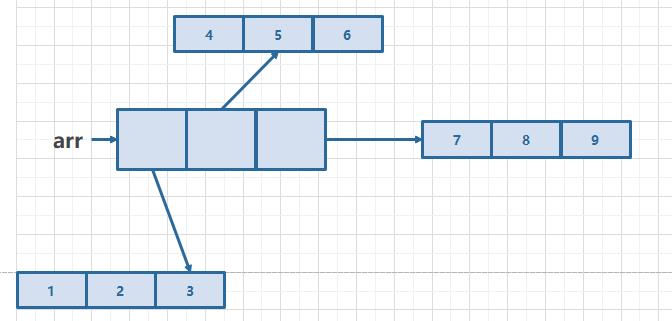
1.3 为什么数组下标是从0开始
在我们编程的过程中,可能会很多次用到arr[0],这样的操作。大家有没有想过,为啥下标index是从0开始呢?
数组的寻址公式:
arr[N] = base_address+N*data_type_size;
base_address:基础地址;
data_type_size:每个数组中元素的大小;比如说int类型,那就是4
比如说:我们当前数组的基础地址是从1000开始,base_address=1000,如果我们想得到数组的第一个地址。那么根据公式:arr[0] = base_address+0*data_type_size=base_address=1000,刚好就在我们开始的位置。
但是如果我们下标从1开始计算,那么如果我想得到第一个数据的地址,根据公式,我们应该进行这样的运算:arr[i] = base_address+(i-1)*data_type_size;此时i>0
有人可能会说了,不就多了个1-1嘛。算出来还不是一样的值。有啥影响呢?
但事实上没那么简单~ 对于我们来说,这种计算可能没有任何影响。但是对于cpu来说,相当于至少多了一条减法指令。有的同学应该看过字节码文件编译之后得到的汇编语言,如下图
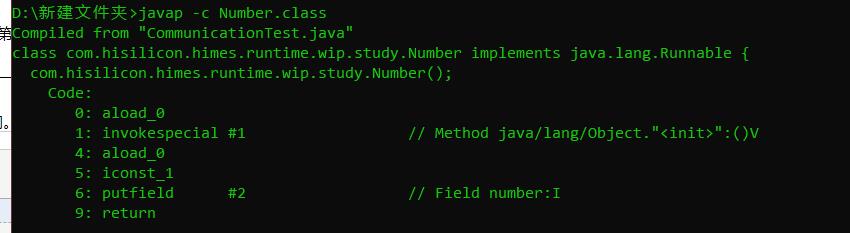
但是有个问题,我们执行的代码其实上最终是于汇编语言转换为机器码语言执行的。但是汇编语言中,我们如果用到了上述的公式操作,这个相当于又多了至少一条指令。指令的操作是会消耗性能。
但是如果从0开始呢?我们就可以避免这种多余的性能消耗。
1.4 时间复杂度
上面大致的介绍了下数组的基本情况,下面进入重点环节-时间复杂度。
对于时间复杂度这个概念,想必很多人都不陌生。
简单来说:预估代码执行时间随着代码规模增长的变化趋势。
如果有的同学不了解的话,可以看看这个帖子,讲的挺详细的:
https://www.cnblogs.com/54chensongxia/p/14012838.html
下面,我们从增删查这三个方向来看看对应的时间复杂度
1.4.1 新增
三种情况:
1.尾部插入
2.中间插入
3.超范围插入
1.4.1.1 尾部插入
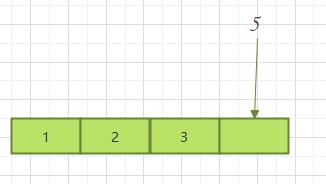
对于尾部插入来说,只需要关注插入数据即可。由于插入的是尾部,所以之前的数据不需要做其他改动。所以时间复杂度是O(1)
1.4.1.2 中间插入
如果想要从中间插入,那么需要将当前下标即后面的数据向后移位。即时间复杂度为0(n)
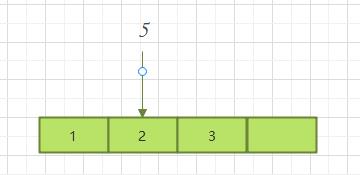
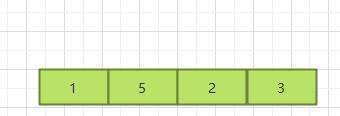
1.4.1.3 超范围插入
超范围插入即当前数组中所有空间都被占满,无法满足再次将数据插入尾部的动作。因此急需要扩容后才能进行操作。数组扩容1.5倍
所以时间复杂度依旧是O(n)
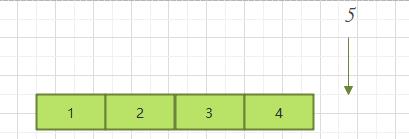
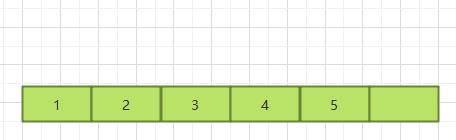
1.4.2 删除
数组的删除分为下标删除和数据删除。
但是不管是通过下标还是数据,其实上内部最终都是通过找到对应的下标位置来进行删除
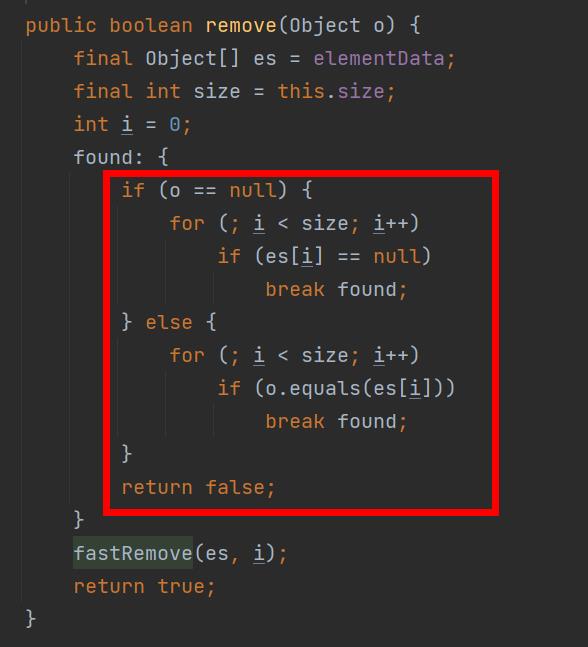
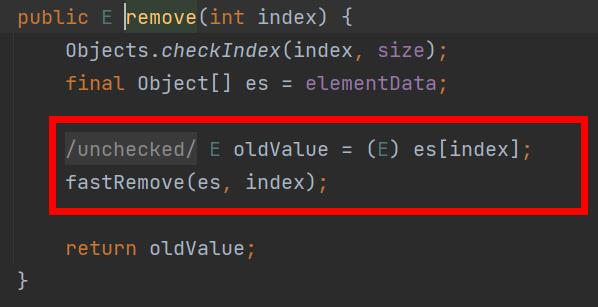
大家有兴趣可以取看看这个执行流程。是理想情况下,使用下标删除的情况下,时间复杂度是O(1)。检查一次通过,然后不需要进行复制,直接设置为null。
但是,时间复杂度应该考虑的更详细一些。我们应该考虑两个模式下的删除情况。比如说使用数据删除,极有可能进行遍历操作(遍历N次),然后进行数组复制,这个时候的时间复杂度就是O(n)。而且这个还是常规情况
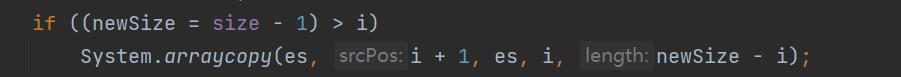
1.4.3 查找
数组是比较适合范围查找的,但是查找的时间复杂度并不是O(1),即便是用二分法查找,时间复杂度也是O(logN)。所以我们在描述的时候要注意这些坑,应该说明:根据下标随机访问的时间复杂度为O(1)
咱们谈论时间复杂度的时候,一定要充分的考虑各种场景。不能想当然,比如说有人问你,数组查询操作的时间复杂度是多少?这时候你要清楚他问的是什么,是范围查询?还是通过下标查询?还是通过数值去查询?
2. 链表
2.1 什么是链表
其实我们认识数组的化就可以很好的认识链表。
数组是什么呢?我们可以把它看做“正规军”,排列有序。
那链表呢?我们可以把它看做“地下党”,为什么是“地下党”呢?上下级联系。我知道我上级的姓名、性别、住址,下级的姓名一切信息我也知道。但是并不是整齐排列的,你很难把我给一锅端了。
2.2 数据结构
2.2.1 单向链表

2.2.2 双向链表

我们可以通过以上的链表结构来直观地了解到刚刚的“地下党”的比喻。
但是呢?毕竟是地下党,为了做事情,就没有那么整齐划一了 ———— 链表的存储方式是随机存储。
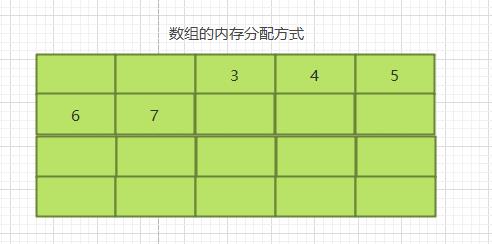
什么是随机存储呢?之前我们讲解了数组的内存分配方式,数组在内存中占用了连续完整的存储空间。而链表则采用了见缝插针的方式。链表的每一个节点分布在内存中不同的位置,依靠next指针关联。这样可以灵活有效的利用零散的碎片空间。
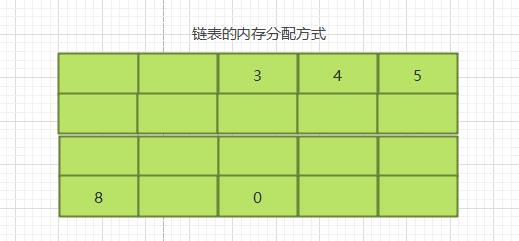
2.3 时间复杂度
2.3.1 查询
在查询数据的时候,链表不像数组那样,可以通过下标快速定位。链表只能从头节点开始向后逐一查找。
所以通常来说时间复杂度为O(N),最好的就是只查了一次为O(1).
2.3.2 插入
头部插入
中间插入
尾部插入
2.3.2.1 头部插入
头部插入可以分为两个步骤
第一步,把新节点的next指针指向原先的头结点
第二步,把新节点变成头结点

2.3.2.2 中间插入
同样分为两步
第一步,新节点的next指针,指向插入位置的节点
第二步,插入位置前置节点的next指针指向新节点
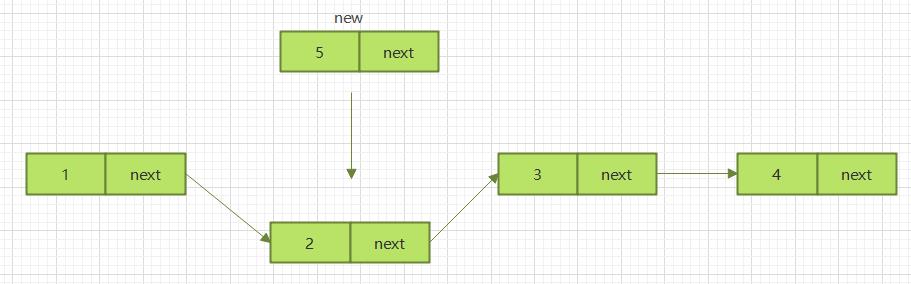
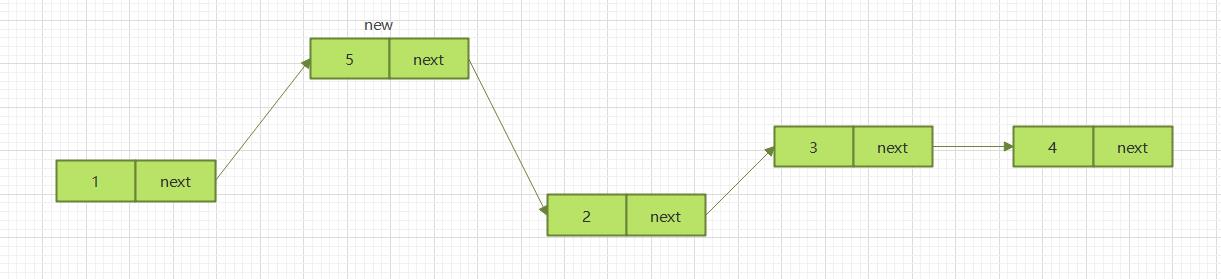
2.3.2.3 尾部插入
直接将节点插入尾部
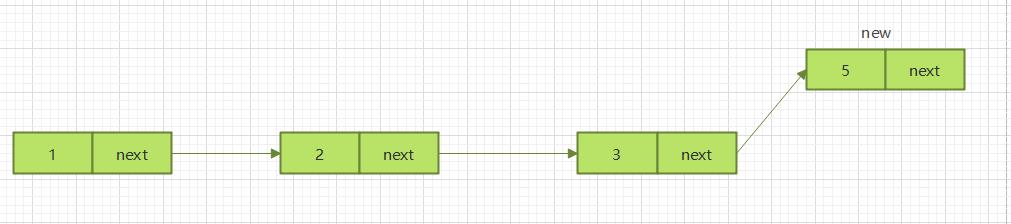
2.3.3 删除
删除同样分为三种情况
头部删除
中间删除
尾部删除
2.3.3.1 头部插入
将链表的头结点设置为原来头节点的next指针

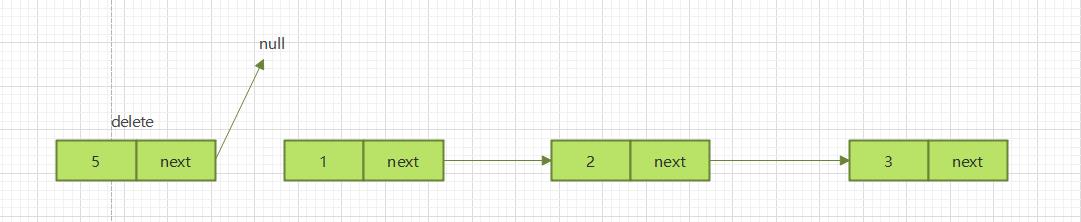
2.3.3.2 中间插入
将需要删除节点的上一节点的next指针指向需要删除节点的下一节点即可
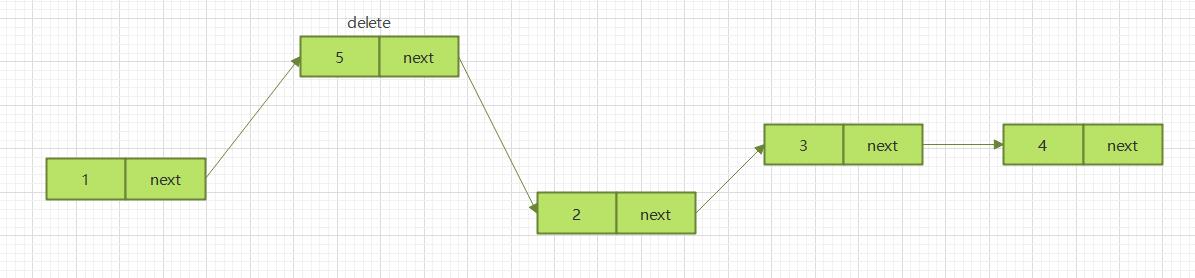
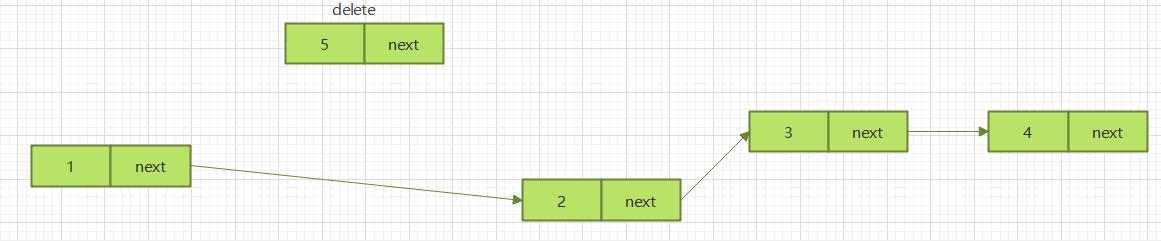
2.3.3.3 尾部插入
将倒数第二个节点的next指针设置为null


至于更新操作,其实和查询操作差不多,就不再做论述
在不考虑插入、删除操作之前查找元素的过程,只考虑纯粹的插入和删除操作,时间复杂度都是O(1)。
时间复杂度不需要去硬记,应该在根据对应场景去分析!!!
总结一下:
| 查找 | 更新 | 新增 | 查询 | |
| 数组 | O(1) | O(1) | O(n) | O(n) |
| 链表 | O(n) | O(n) | O(1) | O(1) |
以上是关于(2021.9.16)针对数组和链表的时间复杂度详解的主要内容,如果未能解决你的问题,请参考以下文章