递归：为运算表达式设计优先级

Posted 2022-11-18 我家大宝最可爱

为运算表达式设计优先级

首先来理解运算表达式，任何运算表达式的基础都是exp op exp，即中间是一个运算符，左侧和右侧分别是一个运算表达式或者数字。举几个具体的例子

1. 左右两侧都是exp，例如(1+2)*(3+4)
2. 两侧都是数字，这个是最简单的，例如5+6
3. 一侧是表达式，一侧是数字，例如(5+6)*7或者8+(9*10)
4. 如果我们认为数字是最小的运算表达式，那么就可以写成通用形式exp op exp

这个问题也是这样的，举个例子5-6*7+8，对于每个运算符都可以考虑成一个运算表达式的形式

1. 对于-号，(5)-(6*7+8)
2. 对于*号，(5-6)*(7+8)
3. 对于+号，(5-6*7)+(8)

这就是我的第一想法，一开始我是觉得，有多少个运算符就有多少个结果。虽然有的子运算表达式比较长，也只不过多谢一个运算符号而已，况且还没有括号，那是非常的简单。但是我看了别人的代码之后，突然发现，一个运算表达式返回的是一个数组，那么子运算表达式的结果应该也是一个数组才对，而不应该是一个单一的数字。例如子运算表达式6*7+8，考虑每个运算符之后又可以写成

1. 对于*号，(6)*(7+8)
2. 对于+号，(6*7)+(8)

这就相当于说5-6*7+8有三种结果，但是其中一种结果又有两种结果，画出流程图可以看到，这其实就是递归。

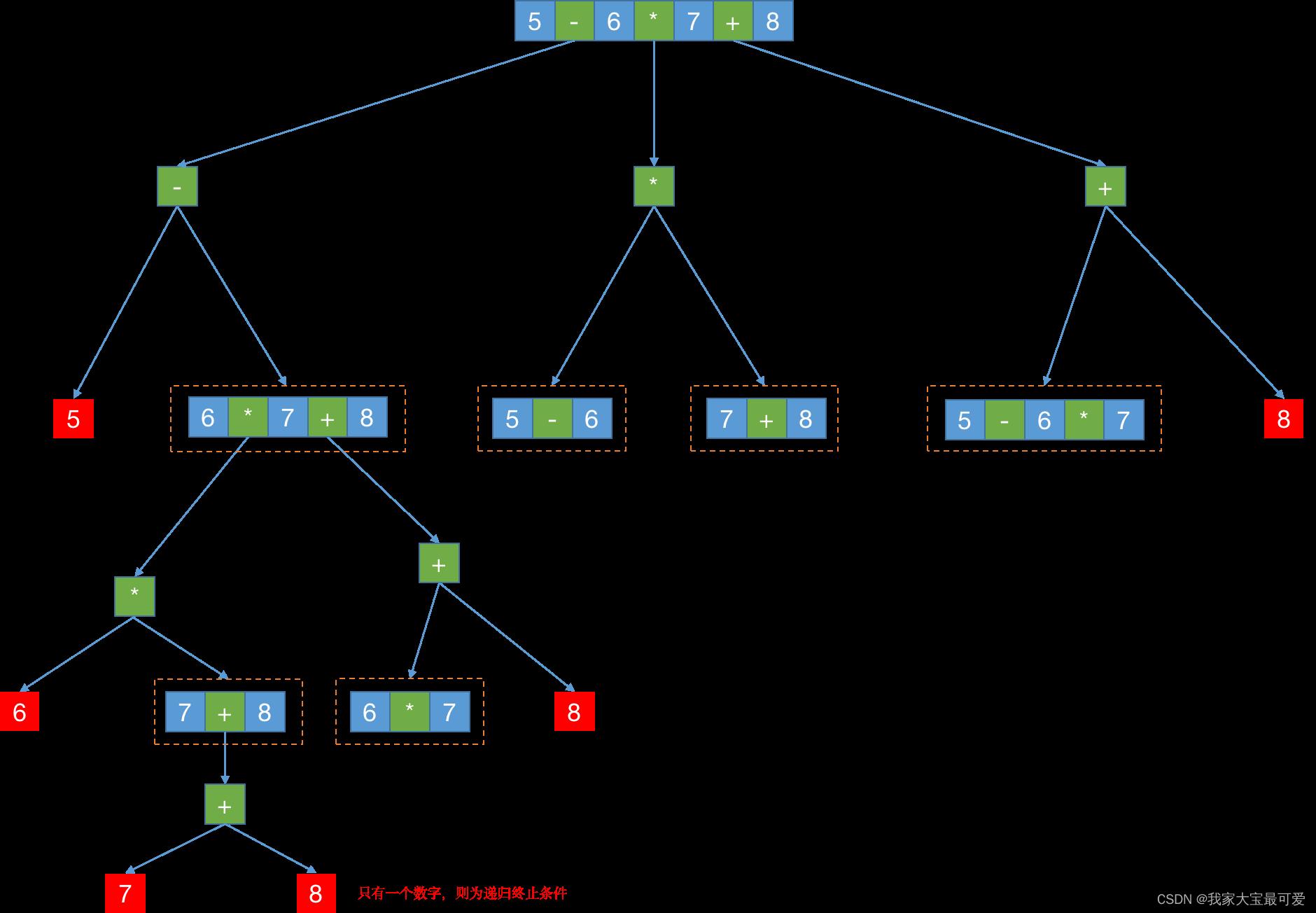
s = "1-2-3"

def dfs(s):
    if s.isdigit():
        return [int(s)]
    res = []
    for i, c in enumerate(s):
        if c in ('+','-','*'):
            lres = dfs(s[:i])
            rres = dfs(s[i+1:])
            for l in lres:
                for r in rres:
                    if c == '+':
                        res.append(l + r)
                    elif c == '-':
                        res.append(l - r)
                    else:
                        res.append(l * r)
    return res


print(dfs(s))

原问题是给定一个运算表达式，返回一个数组，这个数组中是所有可能的运算结果
首先不说怎么做，如果是递归的话，子问题的返回是什么，肯定也是一个数组，因为子问题与原问题是结构是一致的。