Pytorch-张量tensor详解（线性回归实战）

Posted 2022-11-18 吾仄lo咚锵

文章目录

• 创建
• 运算
• 微分
• 实战

张量（tensor）是Pytorch中最基本的操作对象，表示一个多维矩阵，类似numpy中的ndarrays，是可以在GPU上使用以加速运算。

创建

---

直接创建张量：

函数	功能
ones(*sizes)	全1Tensor
zeros(*sizes)	全0Tensor
eye(*sizes)	对⻆线为1，其他为0
arange(s,e,step)	从s到e，步⻓为step
linspace(s,e,steps)	从s到e，均分成steps份
rand/randn(*sizes)	均匀/标准分布
normal(mean,std)	正态分布
randperm(m)	随机排列

import torch

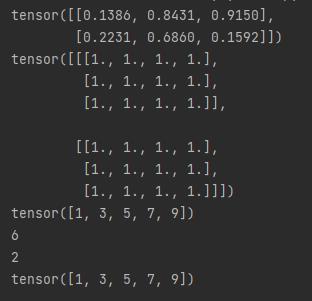
x1 = torch.rand(2, 3)  # 2×3的随机矩阵
print(x1)

x2 = torch.ones(2, 3, 4)  # 2×3×4的全1矩阵
print(x2)

x3 = torch.arange(1, 10, 2)  # 1-10步长2
print(x3)

print(x1.numel())  # 查看元素数量
print(x2.shape[0])  # 查看第0个维度大小
print(x3.data)  # 查看数据

通过数据创建张量：torch.tensor()

import torch
import numpy as np

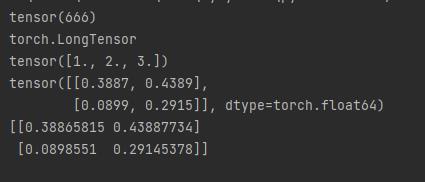
x1 = torch.tensor(666)  # 可以是一个数
print(x1)
print(x1.type())  # 查看数据类型

x2 = torch.tensor([1, 2, 3], dtype=torch.float)  # 创建时指定类型
print(x2)

a = np.random.rand(2, 2)
x3 = torch.from_numpy(a)  # 从numpy创建
print(x3)
print(x3.numpy())  # 转为numpy

运算

---

基本上各种运算都支持，用的时候查一下文档即可，不再赘述。

• 基本运算： add、abs、sqrt、div、exp、fmod、pow、sum、means等
• 三角函数：cos、sin、asin、atan2、cosh等
• 布尔运算： gt、lt、ge、le、eq、ne、topk、sort、max、min等
• 线性计算： trace、diag、mm、bmm、t、dot、cross、inverse、svd等

比如加法就有很多写法：

import torch

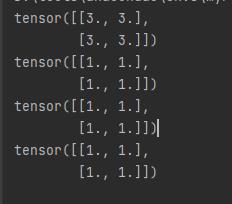
x = torch.zeros(2, 2)  #全0
y = torch.ones(2, 2)  #全1
print(x+3)  # 全部+3
print(x+y)  # x+y
print(x.add(y))  # x+y
x.add_(y)  # 改变原x
print(x)

其他一些运算举例：

import torch

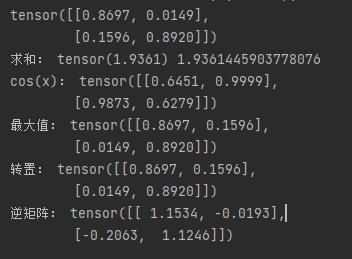
x = torch.rand(2, 2)
print(x)
print("求和：", x.sum(), x.sum().item())  # item打印具体值
print("cos(x)：", x.cos())
print("最大值：", x.t())
print("转置：", x.t())
print("逆矩阵：", x.inverse())

使用view()改变张量形状。

import torch

x = torch.randn(2, 3)  # 2×3
print(x)
print(x.view(3, 2))  # 改成3×2
print(x.view(-1, 1))  # 改成6×1(-1是自动的意思，1是大小)

上述运算中，如果矩阵大小不相同，则会触发广播机制，如：

import torch

x = torch.ones(1, 2)
y = torch.zeros(3, 1)
print(x+y)

由于x是1行2列，而y是3行1列，在运行加法计算时两者大小不一致。此时触发广播机制，将x的第1行广播（复制）到第2行和第3行，扩容成3行2列；同理，y的第1列广播到第2列，也扩容成3行2列。使得大小一致，得以相加，如答案所见。

（插播反爬信息 ）博主CSDN地址：https://wzlodq.blog.csdn.net/

微分

---

若将Torch.Tensor属性requires_ grad设置为True，则Pytorch将开始跟踪对此张量的所有操作。当完成计算后，可以调用backward()并自动计算所有梯度，该张量的梯度将累加到grad属性中。

其实tensor包含了三个属性：data（数据）、grad（梯度）、grad_fn（梯度函数，怎么计算得到的梯度）。

out是一个标量，$out=\frac{d(out)}{dx}$，调用out.backward()便可直接计算，不用指定求导变量。

import torch

x = torch.tensor([1., 2.], requires_grad=True)
print(x.data)  # 数据
print(x.grad)  # 梯度（创建为None
print(x.grad_fn)  # 梯度函数（创建为None
y = x * x
print("y=x*x：", y)
z = y * 3
print("z=y+3：", z)
out = z.mean()  # 求均值
print(out)
out.backward()  # 反向传播
print(x.grad)  # x梯度

$x[1,2]，x_0=1，x_1=2$
$y=x^2=[x_0^2,x_1^2]=[1,4]，y_0=1，y_1=4$
$z=3y=[3y_0,3y_1]=[3,12]，z_0=3，z_1=12$
$out=\frac{3x_0^2+3x_1^2}{2}=\frac{3+12}{2}=7.5$
$\frac{\partial out}{\partial x}=[\frac{\partial out}{\partial x_0},\frac{\partial out}{\partial x_1}]=[3x_0,3x_1]=[3,6]$
手算验证与运行结果一致。

需要特别注意得是，grad是一直累加的，也就是说我们在多轮训练中，每轮调用反向传播后，应把梯度清零，不然影响下一轮求梯度。

x.grad.data.zero_()  # 清理梯度

如果要中断梯度追踪，使用with torch.no_grad():用于调试追踪等，后续需要继续追踪时加下划线设置true即可。

import torch

x = torch.tensor([1., 2.], requires_grad=True)
y1 = x * x
print("y1：", y1.requires_grad)
with torch.no_grad():
    y2 = y1 / 3
    print("y2：", y2.requires_grad)
y3 = y2.sqrt()
print("y3：", y3.requires_grad)
y3.requires_grad_(True)
print("y3：", y3.requires_grad)

实战

---

手动调参和调用模型求解线性回归模型。

import matplotlib.pyplot as plt
import numpy as np
import torch
from torch import nn

# 数据
X = np.linspace(0, 20, 30, dtype=np.float32)
Y = 3 * X + 10 + np.random.rand(30) * 8
Y = Y.astype(np.float32)
plt.scatter(X, Y)
X = torch.from_numpy(X.reshape(-1, 1))
Y = torch.from_numpy(Y.reshape(-1, 1))

# 1.手动调参
w = torch.randn(1, requires_grad=True)  # 权重w
b = torch.randn(1, requires_grad=True)  # 偏置b
learning_rate = 0.001  # 学习率
for epoch in range(1000):
    for x, y in zip(X, Y):
        y_pre = torch.matmul(x, w) + b
        loss = (y - y_pre).pow(2).mean()
        if not w.grad is None:
            w.grad.data.zero_()  # 梯度清零
        if not b.grad is None:
            b.grad.data.zero_()
        loss.backward()  # 反向传播求解梯度
        with torch.no_grad():  # 优化参数
            w.data -= w.grad.data * learning_rate
            b.data -= b.grad.data * learning_rate
print("手动调参：", w, b)
x = X.numpy()
w = w.detach().numpy()
b = b.detach().numpy()
plt.plot(x, w * x + b, color="red", label="手动调参", alpha=0.8)

# 1.调用调参
model = nn.Linear(1, 1)  # 调用线性模型
loss_fn = nn.MSELoss()  # 损失函数均方误差
opt = torch.optim.SGD(model.parameters(), lr=0.001)  # 随机梯度下降
for epoch in range(1000):
    for x, y in zip(X, Y):
        y_pred = model(x)  # 使用模型预测
        loss = loss_fn(y, y_pred)  # 计算损失
        opt.zero_grad()  # 梯度清零
        loss.backward()  # 反向传播求解梯度
        opt.step()  # 优化参数
以上是关于Pytorch-张量tensor详解（线性回归实战）的主要内容，如果未能解决你的问题，请参考以下文章
 
 深度学习-Pytorch张量tensor详解（线性回归实战）
 深度之眼PyTorch训练营第二期 ---2张量操作与线性回归
 Pytorch深度学习实战3-2：什么是张量？Tensor的创建与索引
 Pytorch实现线性回归（手动完成）
 PyTorch框架学习 — Tensor（张量）详解
 [PyTroch系列-12]：PyTorch基础 - 张量Tensor线性运算（点乘叉乘）