统计学习方法笔记-决策树
Posted xiaoranone
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了统计学习方法笔记-决策树相关的知识,希望对你有一定的参考价值。
统计学习方法笔记-决策树
很多集成学习器,他们的基本模型都是决策树,我们经常提到的gbdt模型,它的基模型就是CRAT树.
决策树是什么东西?就是我们平常所说的if-then条件,我们把它组合成树的结构. 决策树中有两种结点,叶子结点和非叶子结点. 其中非叶节点代表的条件,叶子结点表示的实例所属的类别.
我们如何生成这个决策树呢,最主要的一点就是选择那个特征作为当前树的分割结点,这就叫做特征选择,有了特征选择就有了决策树的生成,最后我们还有进行决策树剪枝(后面会提到为什么剪枝).
之前的笔记都没有分析书中的例子,没有一个直观的解释,这次我们从这个例子出发,看一下什么是决策树.
现在我们有下面一张表的数据,想生成一个决策树模型,预测某个人是否符合贷款条件.
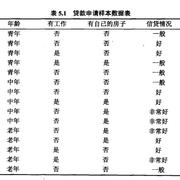
现在假如我们通过"某种方法"构造了一颗下面的决策树. 从下图可以看到特征对应的是非叶子结点,如果这个被分到这个叶节点,就预测为这个叶节点的类别. 从图中我们可以知道以下两点:
- 每一个叶子节点都对应一条从根节点到叶节点的规则,这表示决策树是if-then规则的集合
- 如果一个实例到达了某个叶节点,一定表示它满足了从根节点到该叶子节点的所有条件,而后才得到类别,这不就是先满足条件再得到概率嘛,我们一般叫做条件概率分布.
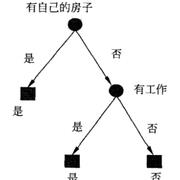
问题来了,为什么我们要选择是否有房子作为第一个构造特征呢?我们构造学习模型,会遵守经验风险最小化或者似然函数极大规则,选择损失函数,我们如何根据风险最小化,选择特征呢?
数据
给定训练数据集
T
=
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
,
(
x
N
,
y
N
)
T=\\(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\\
T=(x1,y1),(x2,y2),...,(xN,yN)
其中,
x
i
=
(
x
i
(
1
)
,
x
i
(
2
)
,
.
.
.
,
x
i
(
n
)
)
T
x_i=(x_i^(1),x_i^(2),...,x_i^(n))^T
xi=(xi(1),xi(2),...,xi(n))T特征向量,n是特征的个数,
y
i
∈
1
,
2
,
.
.
.
,
K
y_i \\in \\1,2,...,K\\
yi∈1,2,...,K表示类别. N是样本个数. 基于这个数据生成决策树模型.
决策树
常见的决策树模型有以下三种(决策树既可以做分类也可以做回归):
- ID3
- C4.5
- CART
先给出两个定义,信息熵和条件熵:
信息熵表示随机变量不确定性的度量,设随机标量X是一个离散随机变量,其概率分布为:
P ( X = x i ) = p i , i = 1 , 2 , . . . , n P(X=x_i)=p_i, i=1,2,...,n P(X=xi)=pi,i=1,2,...,n
则随机变量X的熵定义为:
H ( X ) = − ∑ i = 1 n p i l o g p i H(X)=-\\sum_i=1^np_ilogp_i H(X)=−i=1∑npilogpi
熵越大,随机变量的不确定性就越大,当 p i = 1 n p_i=\\frac1n pi=n1$时,
随机变量的熵最大等于logn,故 0 ≤ H ( P ) ≤ l o g n 0 \\leq H(P) \\leq logn 0≤H(P)≤logn.
条件熵就是在给定X的条件的情况下,随机标量Y的条件,记作 H ( Y ∣ X ) H(Y|X) H(Y∣X),可以结合贝叶斯公式进行理解,定义如下
H ( Y ∣ X ) = ∑ i = 1 n p i H ( Y ∣ X = x i ) H(Y|X)=\\sum_i=1^np_iH(Y|X=x_i) H(Y∣X)=i=1∑npiH(Y∣X=xi)
这里 p i = P ( X = x i ) , i = 1 , 2 , . . . , n p_i=P(X=x_i),i=1,2,...,n pi=P(X=xi),i=1,2,...,n.
一般在基于数据的估计中,我们使用的基于极大似然估计出来的经验熵和经验条件熵.
| model | feature select | 树的类型 | 计算公式 |
|---|---|---|---|
| ID3 | 分类:信息增益 | 多叉树 | g ( D , A ) = H ( D ) − H ( D ∥ A ) g(D,A)=H(D)-H(D\\|A) g(D,A)=H(D)−H(D∥A) |
| C4.5 | 分类:信息增益比 | 多叉树 | g R ( D , A ) = g ( D , A ) H A ( D ) g_R(D,A)=\\fracg(D,A)H_A(D) gR(D,A)=HA(D)g(D,A) |
| CART | 回归:平方误差;分类:基尼指数 | 二叉树 | G i n i ( p ) = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 Gini(p)=\\sum_k=1^Kp_k(1-p_k)=1-\\sum_k=1^Kp_k^2 Gini(p)=∑k=1Kpk(1−pk)=1−∑k=1Kpk2 |
其中, H A ( D ) = H ( D ∣ A ) H_A(D)=H(D|A) HA(D)=H(D∣A).
从表格中,我们总结(ID3,C4.5)决策树算法伪代码:
- 输入:数据集D,特征集合A,阈值e
- 输出:决策树T
- 如果D中所有实例输出同一类 C k C_k Ck, 则T作为单节点树,并将类 C k C_k Ck作为该节点的类标记,返回T;
- 若 A = ∅ A=\\varnothing A=∅,则T为单节点树,将D中实例数最多的类 C k C_k Ck作为该节点的类标记,返回T;
- 否则,根据信息增益(ID3)或者信息增益比(C4.5)计算特征A对D的值,选择当前最优的特征 A g A_g Ag;
- 如果 A g A_g Ag的信息增益小于阈值e,则置T为单节点数,并将D中实例最多的类 C k C_k Ck作为当前的类标记,返回T;
- 否则,根据
A
g
A_g
Ag中的每一个不同的
a
i
a_i
ai,根据
A
g
=
a
i
A_g=a_i
Ag
以上是关于统计学习方法笔记-决策树的主要内容,如果未能解决你的问题,请参考以下文章