matlab Rössler 系统分岔图绘制

Posted 2022-11-12 studyer_domi

1、内容简介

略
598-ref B d 可以交流、咨询、答疑

2、内容说明

分岔图方法很多，这是其中一种

分岔理论或分歧理论(bifurcation theory)是数学中研究一群曲线在本质或是拓扑结构.上的改变。一群曲线可能是向量 场内的积分曲线,也可能是一群类似微分方程的解。
分岔(bifurcation) 常出现在动态系统的数学研究中，是指系统参数(分岔参数)小而连续的变化，结果造成系统本质或是拓扑结构的突然改变。分岔会出现在连续系统(以常微分方程、时滞微分方程或偏微分方程来描述)或是离散系统中(以映射来描述)。
bifurcation-词最早是由儒勒昂利:庞加莱在1885年的论文中提出，这也是第一-篇提到类似特性的数学论文,庞加莱后来也为许多不同的驻点命名而且分类。

3、仿真分析

for a=0.005:0.001:0.38   

    global a b c

% a=0.2;
    b=0.2;
    c=5.7;
    % Initial values of the variables
    uo=[1 1 1]; 

    % Duration of simulation
    tfinal=100;
    tspan=[0 tfinal];

    % Calculation
    options=odeset('InitialStep',1,'MaxStep',1);
    [time, A]=ode45('Rossler',tspan,uo,options);
    x=A(:,1);
    y=A(:,2);
    z=A(:,3); 

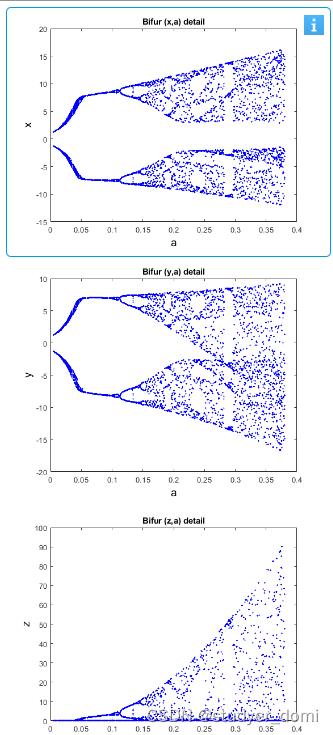
    plot(D1(:,1),D1(:,2),'*','MarkerEdgeColor','b','MarkerSize',1)
    set(gcf,'color','w')
    title('Bifur (x,a) detail')
    xlabel('a','FontName', 'Times New Roman','FontSize',14,'FontWeight','bold','Color','k')
    ylabel('x','FontName', 'Times New Roman','FontSize',14,'FontWeight','bold','Color','k')
    
    figure
    plot(D2(:,1),D2(:,2),'*','MarkerEdgeColor','b','MarkerSize',1)
    set(gcf,'color','w')
    title('Bifur (y,a) detail')
    xlabel('a','FontName', 'Times New Roman','FontSize',14,'FontWeight','bold','Color','k')
    ylabel('y','FontName', 'Times New Roman','FontSize',14,'FontWeight','bold','Color','k')
    
    figure
    plot(D3(:,1),D3(:,2),'*','MarkerEdgeColor','b','MarkerSize',1)
    set(gcf,'color','w')
    title('Bifur (z,a) detail')
    xlabel('a','FontName', 'Times New Roman','FontSize',14,'FontWeight','bold','Color','k')
    ylabel('z','FontName', 'Times New Roman','FontSize',14,'FontWeight','bold','Color','k')

 

4、参考论文

略