OpenCV图像缩放插值之BiCubic双三次插值

Posted 2022-11-11 贺二公子

原文地址：https://blog.csdn.net/duiwangxiaomi/article/details/123845869

---

文章目录

• 图像缩放算法简介
• OpenCV中INTER_CUBIC算法原理
• • 算法流程
  • 算法原理
• CUBIC算法C语言实现
• 结语

图像缩放算法简介

在图像的仿射变换中，很多地方需要用到插值运算，常见的插值运算包括最邻近插值，双线性插值，双三次插值（立体插值），兰索思插值等方法，OpenCV提供了很多方法，其中，双线性插值由于折中的插值效果和运算速度，运用比较广泛。双三次插值效果最好，但速度较慢。

OpenCV中实现图像缩放的函数为

void resize(InputArray src, OutputArray dst, Size dsize, double fx=0, double fy=0, int interpolation=INTER_LINEAR );

参数说明：

• src：输入，原图像，即待改变大小的图像；
• dst：输出，改变大小之后的图像，这个图像和原图像具有相同的内容，只是大小和原图像不一样而已；
• dsize：输出图像的大小。如果这个参数不为0，那么就代表将原图像缩放到这个Size(width，height)指定的大小；如果这个参数为0，那么原图像缩放之后的大小就要通过下面的公式来计算：

  dsize = Size(round(fxsrc.cols), round(fysrc.rows))
  

  其中，fx和fy就是下面要说的两个参数，是图像width方向和height方向的缩放比例。
  fx：width方向的缩放比例，如果它是0，那么它就会按(double)dsize.width/src.cols来计算；
  fy：height方向的缩放比例，如果它是0，那么它就会按照(double)dsize.height/src.rows来计算；
• interpolation：这个是指定插值的方式，图像缩放之后，肯定像素要进行重新计算的，就靠这个参数来指定重新计算像素的方式，有以下几种：
  • INTER_NEAREST - 最邻近插值
  • INTER_LINEAR - 双线性插值，如果最后一个参数你不指定，默认使用这种方法
  • INTER_AREA - 区域插值

    resampling using pixel area relation.
    It may be a preferred method for image decimation, as it gives moire’-free results.
    But when the image is zoomed, it is similar to the INTER_NEAREST method.

  • INTER_CUBIC - 双三次插值，4x4像素邻域内的双立方插值
  • INTER_LANCZOS4 - 8x8像素邻域内的Lanczos插值

OpenCV中INTER_CUBIC算法原理

接下来讲一下INTER_CUBIC - 双三次插值的算法原理。
双三次插值算法是基于周围的4*4=16个像素点，通过计算16个像素点的权重，累积得到增加点的像素值。

算法流程

1. 假设源图像A大小为m * n，缩放K倍后的目标图像B的大小为M*N，即K=M/m；
2. A的每一个像素点是已知的，B是未知的，我们想要求出目标图像B中每一像素点(X,Y)的值，必须先找出像素(X,Y)在源图像A中对应的像素(x,y)；
3. 再根据源图像A距离像素(x,y)最近的16个像素点作为计算目标图像B(X,Y)处像素值的参数；
   利用BiCubic基函数求出16个像素点的权重，图B像素(x,y)的值就等于16个像素点的加权叠加。

算法原理

根据比例关系x/X=m/M=1/K，我们可以得到B(X,Y)在A上的对应坐标为
$$A(x,y)=A(X\ast (m/M),Y\ast (n/N))=A(X/K,Y/K)$$
如图所示P点就是目标图像B在(X,Y)处对应于源图像A中的位置，P的坐标位置会出现小数部分，所以我们假设 P的坐标为P(x+u,y+v)，其中x,y分别表示整数部分，u,v分别表示小数部分（蓝点P1到a11方格中红点的距离）。那么我们就可以得到如图所示的最近16个像素的位置，在这里用a(i,j)(i,j=0,1,2,3)来表示，如下图，图中方格为单个像素的尺寸，红点为像素中心。

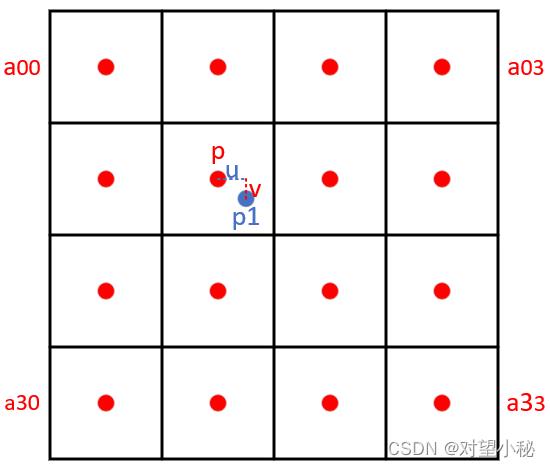
双立方插值的目的就是通过找到一种关系，或者说系数，可以把这 16 个像素对于 P 处像素值的影响因子找出来，从而根据这个影响因子来获得目标图像对应点的像素值，达到图像缩放的目的。

BiCubic基函数形式如下

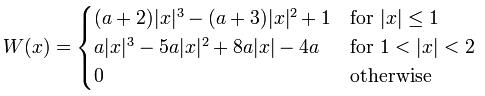
BiCubic函数图像如下

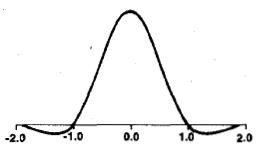
我们要做的就是求出BiCubic函数中的参数x,从而获得上面所说的16个像素所对应的权重W(x)。
BiCubic基函数是一维的，而像素是二维的，所以我们将像素点的行与列分开计算。
BiCubic函数中的参数x表示该像素点到P点的距离。

例如a00距离P(x+u,y+v)的距离为(1+u,1+v)，因此a00的纵坐标权重i_0=W(1+v)，横坐标权重j_0=W(1+u)，a00对B(X,Y)的贡献值为：
$$（a00像素值）\ast i_0\ast j_0$$
因此，a0X的横坐标权重分别为W(1+u)，W(u)，W(1-u)，W(2-u)；ay0的纵坐标权重分别为W(1+v)，W(v)，W(1-v)，W(2-v)；B(X,Y)像素值为：

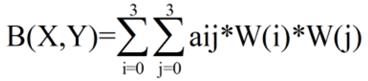
CUBIC算法C语言实现

// im-原图指针	w-原图宽		h-原图高
// s_im-目标图像指针		w-目标图像宽		h-目标图像高
const int ErrorCode_imdataProc =-1000000;
int vcImageSimpleSamplingRoi(unsigned char * im, int w, int h, 
	unsigned char * s_im, int s_w, int s_h)

	int ret = 0;

	float fWStep = 0.0f, fHStep = 0.0f;

	int ii = 0, jj = 0;

	unsigned char * pCurr = 0;
	unsigned char * pSamp = 0;
	
	const float A = -0.75f;
	float coeffsX[4], coeffsY[4];
	float fx = 0.0f, fy = 0.0f;
	int sx = 0, sy = 0, iscale_x = 0, iscale_y = 0;
	short cbufX[4], cbufY[4];
	int sum = 0;
	int mm = 0, nn = 0;
	
	if (NULL == im || w <= 0 || h <= 0 ||
		NULL == s_im || s_w <= 0 || s_h <= 0) 
		ret = ErrorCode_imdataProc - 4;
		goto nExit;
	

	fWStep = 1.0f * roi.width / s_w;
	fHStep = 1.0f * roi.height / s_h;
	pSamp = s_im;

	for (ii = 0; ii < s_h; ++ii)
	
		fy = (float)((ii + 0.5)*fHStep - 0.5);
		sy = vcFloor(fy);
		fy -= sy;

		if (sy < 1)
			fy = 0, sy = 1;
		

		if (sy >= roi.height- 3)
			fy = 0, sy = roi.height - 3;
		

		coeffsY[0] = ((A*(fy + 1) - 5*A)*(fy + 1) + 8 * A)*(fy + 1) - 4 * A;
		coeffsY[1] = ((A + 2)*fy - (A + 3))*fy*fy + 1;
		coeffsY[2] = ((A + 2)*(1 - fy) - (A + 3))*(1 - fy)*(1 - fy) + 1;
		coeffsY[3] = 1.f - coeffsY[0] - coeffsY[1] - coeffsY[2];

		cbufY[0] = (short)(coeffsY[0] * 2048);
		cbufY[1] = (short)(coeffsY[1] * 2048);
		cbufY[2] = (short)(coeffsY[2] * 2048);
		cbufY[3] = (short)(coeffsY[3] * 2048);

		for (jj = 0; jj < s_w; ++jj)
		
			fx = (float)((jj + 0.5)*fWStep - 0.5);
			sx = vcFloor(fx);
			fx -= sx;

			if (sx < 1)
				fx = 0, sx = 1;
			

			if (sx >= roi.width- 3)
				fx = 0, sx = roi.width- 3;
			
			
			coeffsX[0] = ((A*(fx + 1) - 5*A)*(fx + 1) + 8*A)*(fx + 1) - 4*A;
			coeffsX[1] = ((A + 2)*fx - (A + 3))*fx*fx + 1;
			coeffsX[2] = ((A + 2)*(1 - fx) - (A + 3))*(1 - fx)*(1 - fx) + 1;
			coeffsX[3] = 1.f - coeffsX[0] - coeffsX[1] - coeffsX[2];
			
			cbufX[0] = (short)(coeffsX[0] * 2048);
			cbufX[1] = (short)(coeffsX[1] * 2048);
			cbufX[2] = (short)(coeffsX[2] * 2048);
			cbufX[3] = (short)(coeffsX[3] * 2048);

			sum = 0;
			for (mm = 0; mm < 4; ++mm)//rows
			
				pCurr = im + (roi.y + sy + mm - 1) * w + roi.x;
				for (nn = 0; nn < 4; ++nn)//cols
				
					sum += pCurr[sx + nn - 1] * cbufY[mm]*cbufX[nn];
				
			
			pSamp[jj] = sum >> 22;
		
		pSamp += s_w;
	

	ret = 1;
nExit:
	return ret;

结语

以上为OpenCV图像缩放插值之BiCubic双三次插值的原理及实现。如还有不懂，可参考下面的参考链接，都是很不错的文章。

参考链接：

1. OpenCV中resize函数五种插值算法的实现过程
2. OpenCV ——双线性插值（Bilinear interpolation）
3. C++ OpenCV实现图像双三次插值算法详解
4. 双三次插值（BiCubic插值）
5. 图像插值算法之双三次插值
6. BiCubic Interpolation
7. OpenCV图像缩放resize各种插值方式的比较
8. aitken插值方法的c++代码_双三次插值算法的C++实现与SSE指令优化