Java:最通俗易懂地理解0-1背包问题
Posted 方舟aark
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Java:最通俗易懂地理解0-1背包问题相关的知识,希望对你有一定的参考价值。
Reference: https://www.jianshu.com/p/a66d5ce49df5
- 问题:
0-1背包问题:给定n种物品和一背包。物品 i 的重量似乎 wi,其价值为 vi,背包的容量为 c。问应该如何选择装入背包中的物品,使得装入背包中物品的总价值最大?
- 通俗解答:
假设你是一个小偷,背着一个可装下4磅东西的背包,你可以偷窃的物品如下:

为了让偷窃的商品价值最高,你该选择哪些商品?
1、简单算法
最简单的算法是:尝试各种可能的商品组合,并找出价值最高的组合。

这样显然是可行的,但是速度非常慢。在只有3件商品的情况下,你需要计算8个不同的集合;当有4件商品的时候,你需要计算16个不同的集合。每增加一件商品,需要计算的集合数都将翻倍!这种算法的运行时间是O(2ⁿ),真的是慢如蜗牛。
2、动态规划
解决这样问题的答案就是使用动态规划!下面来看看动态规划的工作原理。动态规划先解决子问题,再逐步解决大问题。
对于背包问题,你先解决小背包(子背包)问题,再逐步解决原来的问题。

比较有趣的一句话是:每个动态规划都从一个网格开始。
背包问题的网格如下:

网格的各行为商品,各列为不同容量(1~4磅)的背包。所有这些列你都需要,因为它们将帮助你计算子背包的价值。
网格最初是空的。你将填充其中的每个单元格,网格填满后,就找到了问题的答案!
后面会列出计算这个网格中单元格值得公式,但现在我们先来一步一步做。首先来看第一行。

这是吉他行,意味着你将尝试将吉他装入背包。在每个单元格,都需要做一个简单的决定:偷不偷吉他?别忘了,你要找出一个价值最高的商品集合。
第一个单元格表示背包的的容量为1磅。吉他的重量也是1磅,这意味着它能装入背包!因此这个单元格包含吉他,价值为1500美元。
下面来填充网格。

与这个单元格一样,每个单元格都将包含当前可装入背包的所有商品。
来看下一个单元格。这个单元格表示背包容量为2磅,完全能够装下吉他!

这行的其他单元格也一样。别忘了,这是第一行,只有吉他可供你选择,换而言之,你假装现在还没发偷窃其他两件商品。
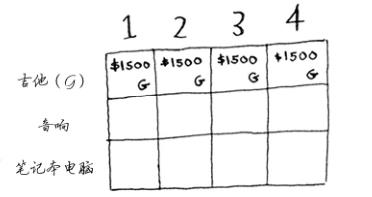
此时你很可能心存疑惑:原来的问题说的额是4磅的背包,我们为何要考虑容量为1磅、2磅等得背包呢?前面说过,动态规划从小问题着手,逐步解决大问题。这里解决的子问题将帮助你解决大问题。

别忘了,你要做的是让背包中商品的价值最大。这行表示的是当前的最大价值。它指出,如果你有一个容量4磅的背包,可在其中装入的商品的最大价值为1500美元。
你知道这不是最终解。随着算法往下执行,你将逐步修改最大价值。
我们来填充下一行——音响行。你现在处于第二行,可以偷窃的商品有吉他和音响。
我们先来看第一个单元格,它表示容量为1磅的背包。在此之前,可装入1磅背包的商品最大价值为1500美元。
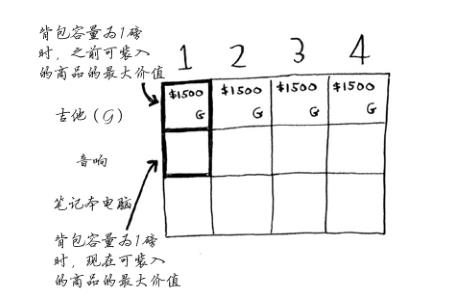
该不该偷音响呢?
背包的容量为1磅,显然不能装下音响。由于容量为1磅的背包装不下音响,因此最大价值依然是1500美元。

接下来的两个单元格的情况与此相同。在这些单元格中,背包的容量分别为2磅和3磅,而以前的最大价值为1500美元。由于这些背包装不下音响,因此最大的价值保持不变。
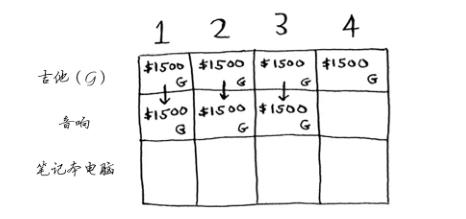
背包容量为4磅呢?终于能够装下音响了!原来最大价值为1500美元,但如果在背包中装入音响而不是吉他,价值将为3000美元!因此还是偷音响吧。


下面以同样的方式处理笔记本电脑。笔记本电脑重3磅,没法将其装入1磅或者2磅的背包,因此前两个单元格的最大价值仍然是1500美元。


对于容量为4磅的背包,情况很有趣。这是非常重要的部分。当前的最大价值为3000美元,你可不偷音响,而偷笔记本电脑,但它只值2000美元。

你可能始终心存疑惑:为何计算小背包可装入的商品的最大价值呢?但愿你现在明白了其中的原因!余下了空间时,你可根据这些子问题的答案来确定余下的空间可装入哪些商品。笔记本电脑和吉他的总价值为3500美元,因此偷它们是更好的选择。
最终的网格类似于下面这样。


3、代码实现:
/**
* @author:我没有三颗心脏
* @create:2017-11-14-10:24
*/
public class MaxBag
static int n; // 描述物品个数
static int c; // 描述背包容量
static int[] value; // 描述物品价值
static int[] weight; // 描述物品重量
public static void main(String[] args)
// 初始赋值操作
value = new int[]1500, 3000, 2000;
weight = new int[]1, 4, 3;
c = 4;
n = 3;
// 构造最优解的网格:3行4列
int[][] maxValue = new int[n][c];
for (int i = 0; i < n; i++)
for (int j = 0; j < c; j++)
maxValue[i][j] = 0;
// end for
// 填充网格
for (int i = 0; i < n; i++)
for (int j = 1; j <= c; j++)
if (i == 0)
maxValue[i][j - 1] = (weight[i] <= j ? value[i] : 0);
else
int topValue = maxValue[i - 1][j - 1]; // 上一个网格的值
int thisValue = (weight[i] <= j ? // 当前商品的价值 + 剩余空间的价值
(j - weight[i] > 0 ? value[i] + maxValue[i - 1][j - weight[i]] : value[i])
: topValue);
// 返回 topValue和thisValue中较大的一个
maxValue[i][j - 1] = (topValue > thisValue ? topValue : thisValue);
// end if
// end inner for
// end outer for
// 打印结果二维数组maxValue
for (int i = 0; i < n; i++)
for (int j = 0; j < c; j++)
System.out.printf("%6d", maxValue[i][j]);
System.out.println();

4、额外惊喜
假设你发现还有第四件商品可偷——一个iPhone!(或许你会毫不犹豫的拿走,但是请别忘了问题的本身是要拿走价值最大的商品)

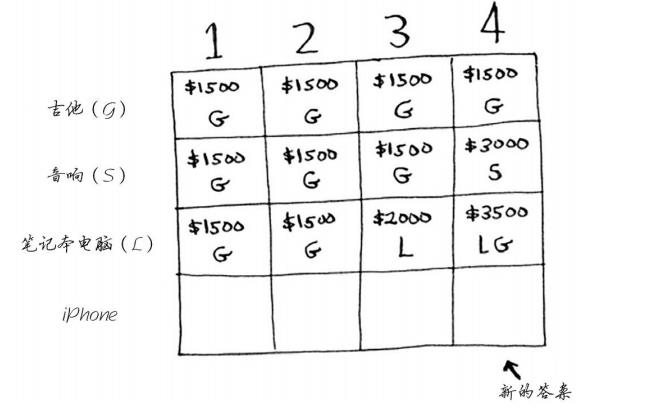
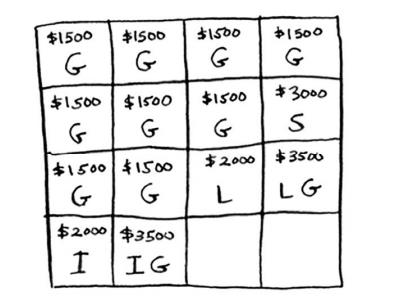
对于第三个单元格,也没有比装入iPhone和吉他更好的选择了。
对于最后一个单元格,情况比较有趣。当前的最大价值为3500美元,但你可以偷iPhone,这将余下3磅的容量。
3磅容量的最大价值为2000美元!再加上iPhone价值2000美元,总价值为4000美元。新的最大价值诞生了!
最终的网格如下。

以上是关于Java:最通俗易懂地理解0-1背包问题的主要内容,如果未能解决你的问题,请参考以下文章