算法概述-第二节:NP完全性理论
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法概述-第二节:NP完全性理论相关的知识,希望对你有一定的参考价值。
文章目录
一:易解、难解和不可解问题基本概念
(1)易解、难解和不可解问题
问题的计算复杂性可以通过解决该问题所需计算量的多少来度量
- 易解问题(East Problem):能够在多项式时间算法解决的问题;例如查找、排序等
- 难解问题(Hard Problem):需要指数时间算法解决的问题;例如TSP问题,Hamilton问题等
- 不可解问题(Unsoluable Problem):不能用计算机求解(无论耗费多少时间)的问题;例如图灵停机问题
(2)多项式时间算法与指数时间算法差别
它们的区别如下
- 二者随问题规模的时间复杂度增长率存在差别:多项式时间复杂度算法是可使用算法;指数时间复杂性算法只有当问题规模足够小时才是可使用的算法
- 计算机性能的提高对多项式时间算法和指数时间算法的影响不同
- 渐近阶意义下的时间复杂性函数忽略了系数和低阶项,但不影响易解问题和难解问题的划分
(3)难解问题现状
难解问题目前未找到有效的多项式时间复杂度算法,目前倾向于接受这类问题是NPC问题和NP难题,不存在有效多项式算法这一猜想。这类问题的大型实例不能用精确算法求解,可以尝试寻求这类问题的有效的近似算法
二:判定问题
判定问题仅仅要求回答是或否的问题,判定问题的重要特性在于:验证一个问题的可行解要比生成一个问题的最优解更容易
三:P问题和NP问题
(1)确定性算法和P类问题
确定性算法:设 A A A是某待求解问题的一个算法,如果在算法整个执行过程中,每一步只有一个确定选择,则称算法 A A A是确定性算法
P类问题(P-Polynomial):如果对于某个判定问题,存在一个非负整数 k k k,对于输入规模为 n n n的实例,能够以 O ( n k ) O(n^k) O(nk)的时间运行一个确定性算法,得到肯定或否定答案,则该判定问题是一个P类问题。所有在多项式时间内求解的判定问题构成P类问题
(2)非确定性算法和NP类问题
非确定性算法:设 A A A是某待求解问题的一个算法,如果算法 A A A以如下猜测并验证的方式工作,就称算法 A A A是非确定性的
- 猜测阶段:该阶段,对问题的输入实例产生一个任意字符串 y y y,算法每一次运行时,串 y y y的值可能不同,即猜测以一种非确定的形式工作
- 验证阶段:该阶段用一个确定性算法验证;①检查在猜测阶段产生的串 y y y是否为合适形式,如果不是,则算法停下来并得到否定结论;②如果串 y y y是合适的形式,则验证它是否是问题的解,如果是,则算法停下来并得到肯定,否则算法停下来并得到否定结论
NP类问题(P-Polynomial):如果对于某个判定问题,存在一个非负整数 k k k,对于输入规模为 n n n的实例,能够以 O ( n k ) O(n^k) O(nk)的时间运行一个非确定性算法,得到肯定或否定答案,则该判定问题是一个NP类问题。所有在非确定性多项式问题内求解的判定问题构成NP类问题
- 关键在于:验证阶段存在一个确定性算法,能够以多项式时间来检查和验证猜测阶段所产生的答案
(3)P与NP
P类问题和NP类问题的主要差别在于:
- P类问题可用多项式时间的确定性算法来进行判定或求解
- NP类问题可用多项式时间的非确定性算法来进行判定或求解
另外,所有的P类问题都是NP问题,也就是说能在多项式时间解决一个问题必然也能在多项式时间内验证一个问题的解。但是P=NP这个等式是否成立至今还未被证明
- 人们猜测 P ≠ N P P\\not =NP P=NP:即存在一个多项式时间的非确定性算法,却不一定能够构造一个多项式时间的确定性算法,来对它进行求解或判定
四:NP完全问题
NP完全(NPC)问题:对于一个判定问题,如果该问题属于NP类问题,但是不知道该问题是否存在多项式时间的确定算法,同时也不能证明这类问题的任何一个不存在多项式时间的确定算法,则称该问题为一个NPC问题
- 目前还未找到一个NPC问题的多项式时间确定性算法
- NPC问题是NP类问题中最难的一个子类
P类、NP类和NPC问题关系如下
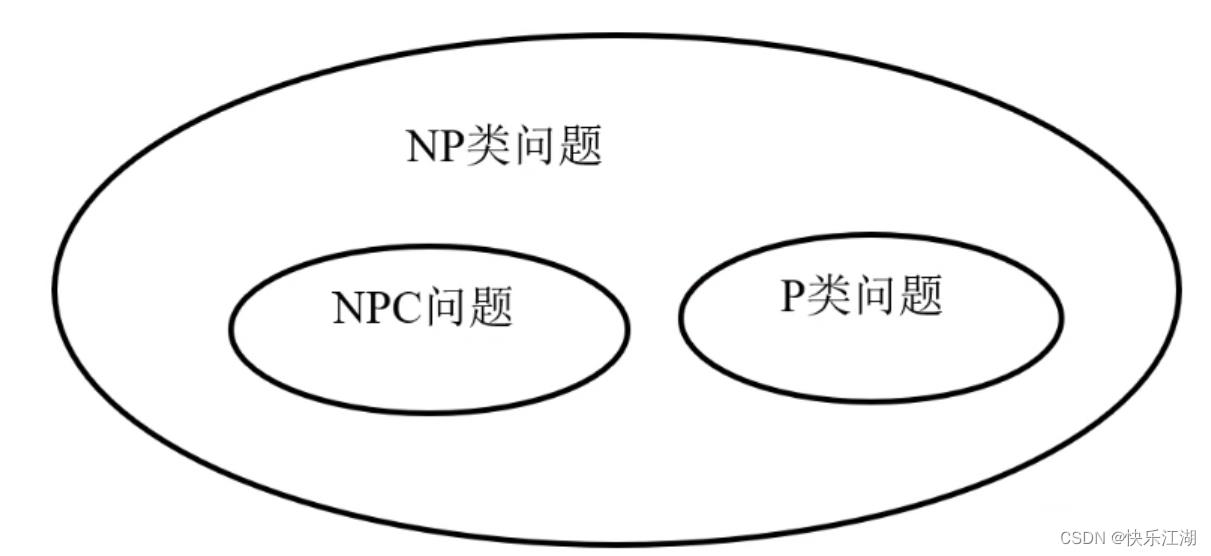
五:典型的NPC问题
①:SAT问题

②:最大团问题

③:图着色问题

④:哈密顿回路问题

⑤:TSP问题

⑥:顶点覆盖问题

⑦:最长路径问题

⑧:子集和问题

六:Cook定理
Cook定理:布尔表达式的可满足性问题SAT是NP完全的。Cook定理给出了第一个NP完全问题,为NPC问题的发现奠定了基础。以SAT为基础,人们很快又证明了很多其他NP完全问题,逐渐形成了一颗以SAT为根的NP完全树。这棵树的每个结点都是一个NP完全问题,该问题可在多项式时间内转化为它的任意儿子结点所表示的问题
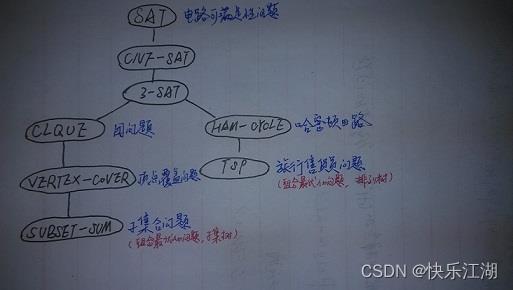
以上是关于算法概述-第二节:NP完全性理论的主要内容,如果未能解决你的问题,请参考以下文章