Optimization of DQN
Posted Harris-H
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Optimization of DQN相关的知识,希望对你有一定的参考价值。
Optimization of DQN
1.Experience Replay


回顾TD算法。
1.1普通TD算法的缺点
我们直到每次更新网络参数 w w w 是通过一次transition,再使用后,我们便会丢弃该经验,这是一种浪费。

每次更新都是通过相邻两个状态转移,相邻两个状态具有强相关性,对实际动作的策略指导会存在问题。
1.2 介绍
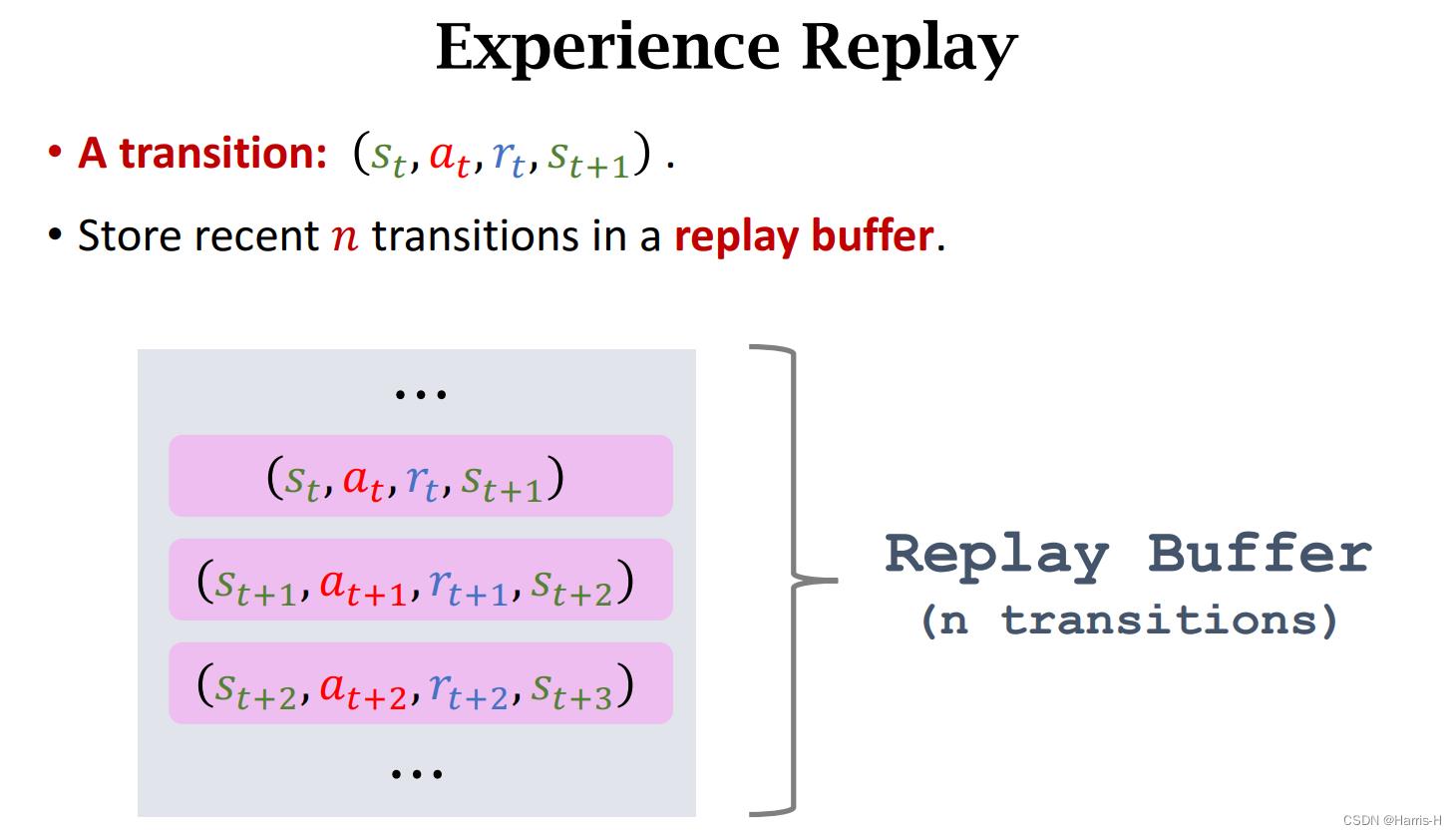
Experience Replay 采用一个Replay Buffer 存储 n n n个transition。

buffer中的transition 保存的是最近的n个,类似LRU(?)

再更新参数时,我们每次从buffer中随机抽样一个或多个(对应multi step) transition,然后计算TD error,然后SGD更新 w w w
1.3 优点

1.减弱强相关性。
2.重复利用experience。
1.4 Prioritized Experience Replay

因为每个transition 重要性是不同的,比如右边的transition 就很难学习到,因此更重要。

可以考虑用TD error 近似优先级,因为越重要就越难学习到,因此error会 越大。

第一种方法将其抽样概率 p t p_t pt 正比TD error 加上 超参数 ϵ \\epsilon ϵ ,该参数是保证概率 > 0 >0 >0
第二种是反比按照TD error 排序后的排名。

为保证网络的均匀稳定,当使用优先经验回放时,学习率 α \\alpha α 应该调整,因为抽样概率不同。

设置函数 ( n p t ) − β (np_t)^-\\beta (npt)−β 这样可以使高重要性的transitions 有低的学习率。

如果新收集的transition,设置 δ t \\delta_t δt 为最大,这样优先级最高,先更新其TD errror。每次我们对抽样的transitions的TD errror进行更新,使得误差更小。

2.Target Network and Double DQN


使用DQN 中的 Q Q Q函数得到 y t y_t yt 更新 Q Q Q,会导致自举问题。
2.1 高估的原因

DQN高估动作价值的原因有:
1.最大化,在进行TD 算法时计算TD target 会对 Q Q Q所有的 a a a取 max \\max max。
因此导致 y t y_t yt 大于真实值。
2.自举,用估计值来反向传播。

根据数学证明可知,在噪声均值为0的分布下得到的 Q Q Q 的最大值期望会更大。

因此会导致高估 q q q

而高估的 y t y_t yt 会进一步更新 Q Q Q 导致高估的影响不断增大。

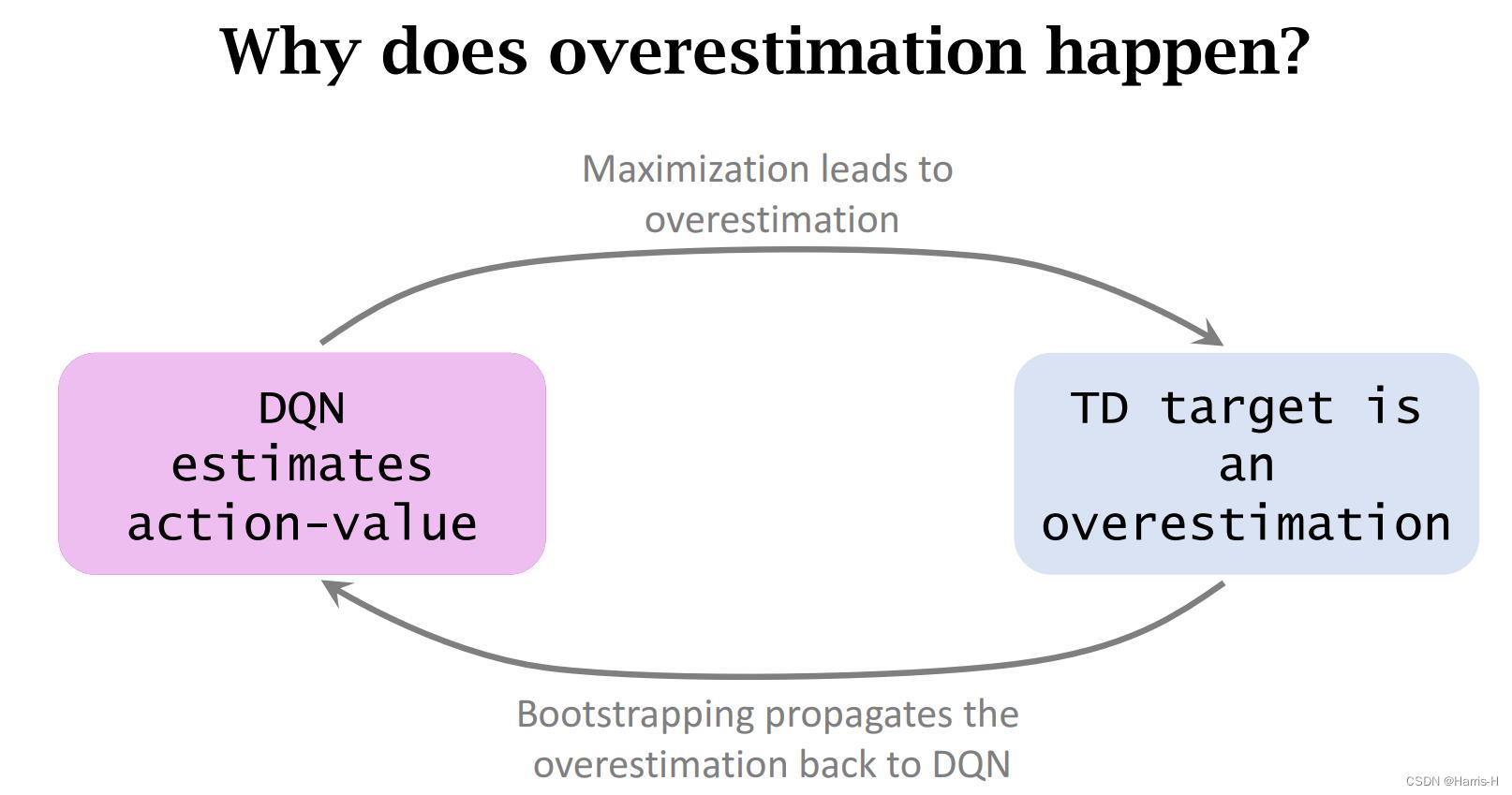
两重影响。
2.2 高估有危害的原因

如果是均匀的高估,对于动作的选择没有影响,因为动作的选择是根据动作打分的相对大小,选取相对最大的进行执行。

但是如果高估不是均匀的,则可能会导致选择错误的动作。

因为 ( s , a ) (s,a) (s,a) 在replay buffer中出现的频率不是均匀的,出现次数越多, Q ( s , a ; w ) Q(s,a;w) Q(s,a;w)的高估就越明显。

2.3 Target Network

用一个DQN 控制agent 执行动作和收集experience,再使用一个DQN Q ( s , a ; w − ) Q(s,a;w^-) Q(s,a;w−) 计算TD target。


更新target network 有两种方法:
1.使用DQN之前的 w w w更新。
2.使用两者的加权平均。

相比naive update,target network 减缓了自举带来的高估。
2.4 Double DQN

这是target network 更新的方法,使用target network选择 a ∗ a^* a∗,用target network更新 y t y_t yt。但是不能完全消除高估。

Double DQN类似于naive update 和 target network 的一种优化。
它使用DQN来选择 a ∗ a^* a∗ ,然后用target network 计算 y t y_t yt ,将selection 与 evaluation 分隔开。
使用Double DQN的
Q
(
s
t
+
1
,
a
∗
,
;
w
−
)
≤
m
a
x
a
Q
(
s
t
+
1
,
a
;
w
−
)
Q(s_t+1,a^*,;w^-)\\le max_aQ(s_t+1,a;w^-)
Q(st+1,a∗,;w−)≤maxaQ(st+1,a;w−)
因此target network 使用自己的
Q
Q
Q计算动作
a
∗
a^*
a∗,选取的是最大的。
而Double DQN不是target network最大的 a ∗ a^* a∗,而是DQN里的最优的。
2.5 Summary

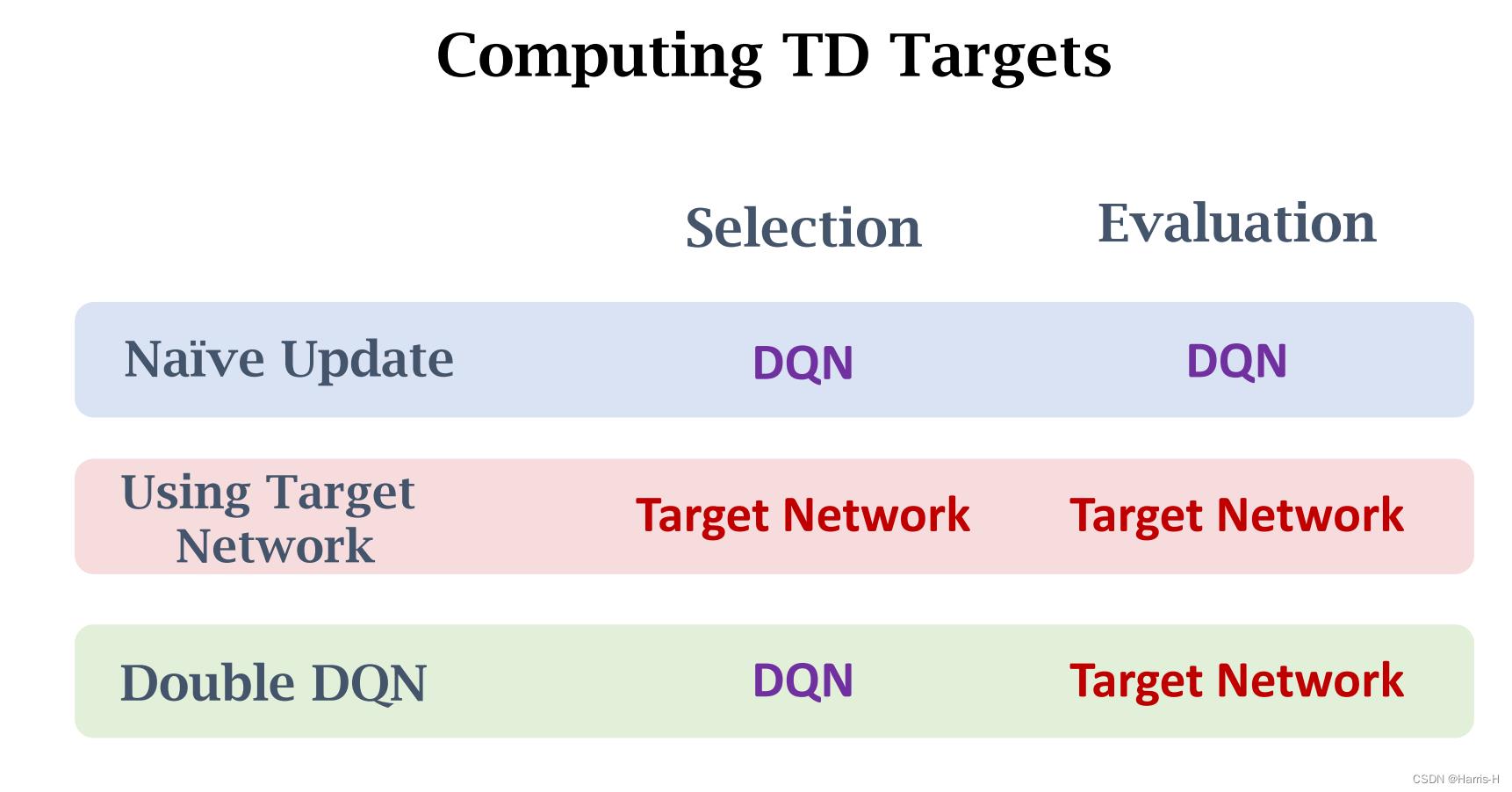
从该图可以看出,结合趋于平衡往往是最优的。
3.Dueling Network
3.1 相关定义

回顾几个定义。

这里定义最优优势函数 A ∗ A^* A∗ 为 Q ∗ Q^* Q∗ 与 V ∗ V^* V∗ 的差值。
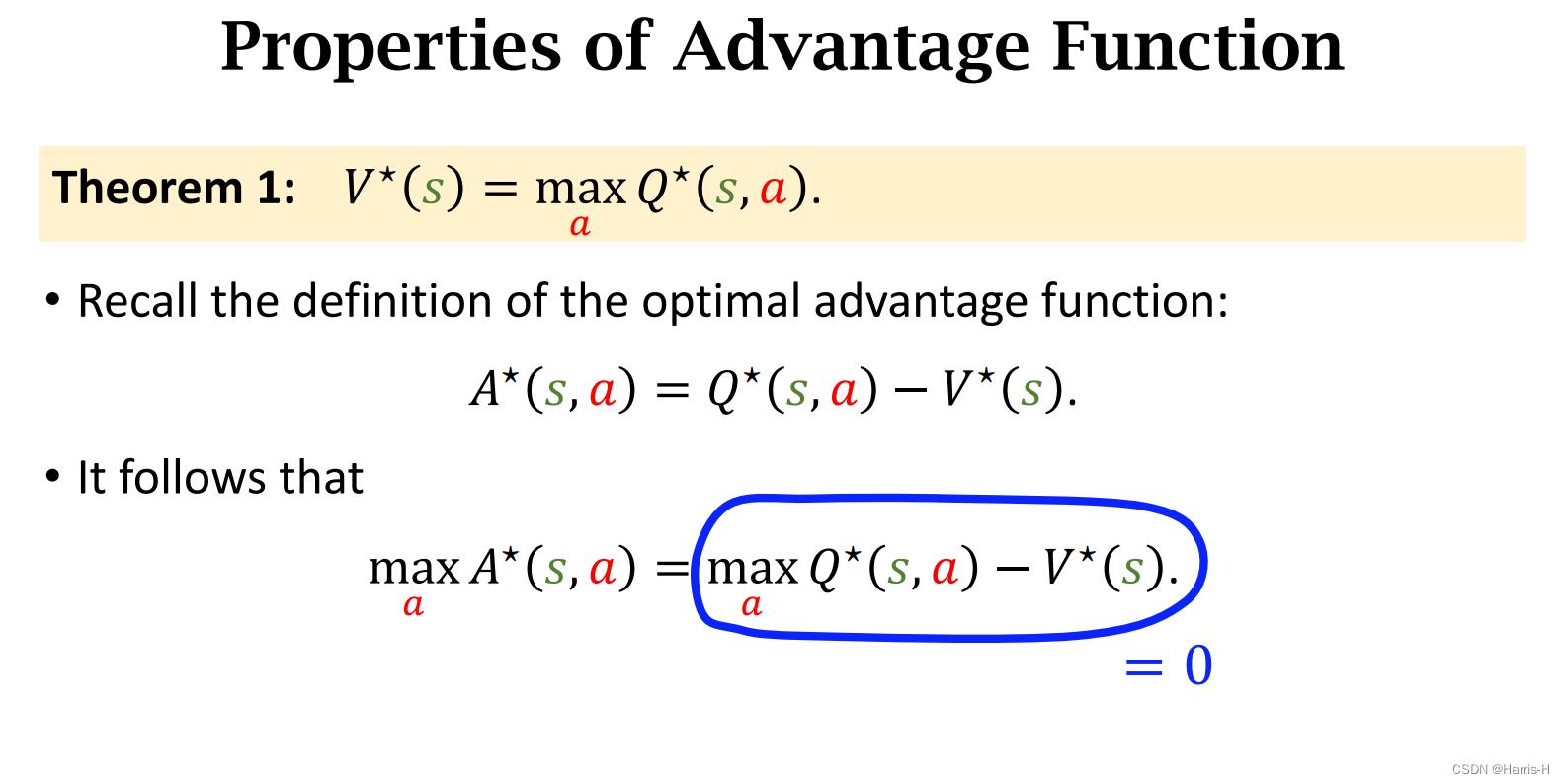
定理1,显然最优的 V V V 是取得所有 a a a 后的 Q ∗ Q^* Q∗

因此可以得到 m a x a A ∗ ( s , a ) = 0 max_aA^*(s,a)=0 maxaA∗(s,a)=0
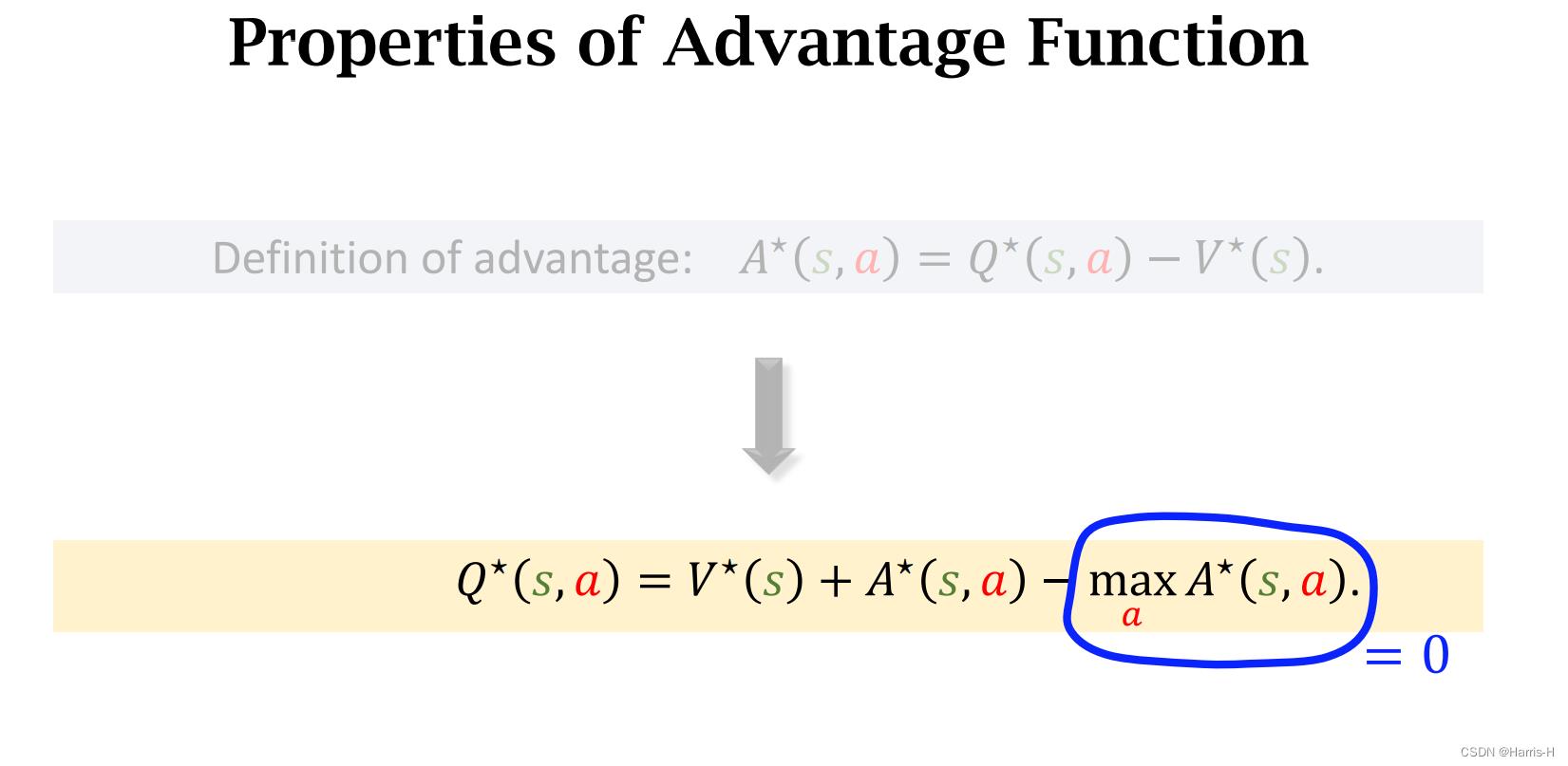
因此可以这样表示 Q ∗ Q^* Q∗
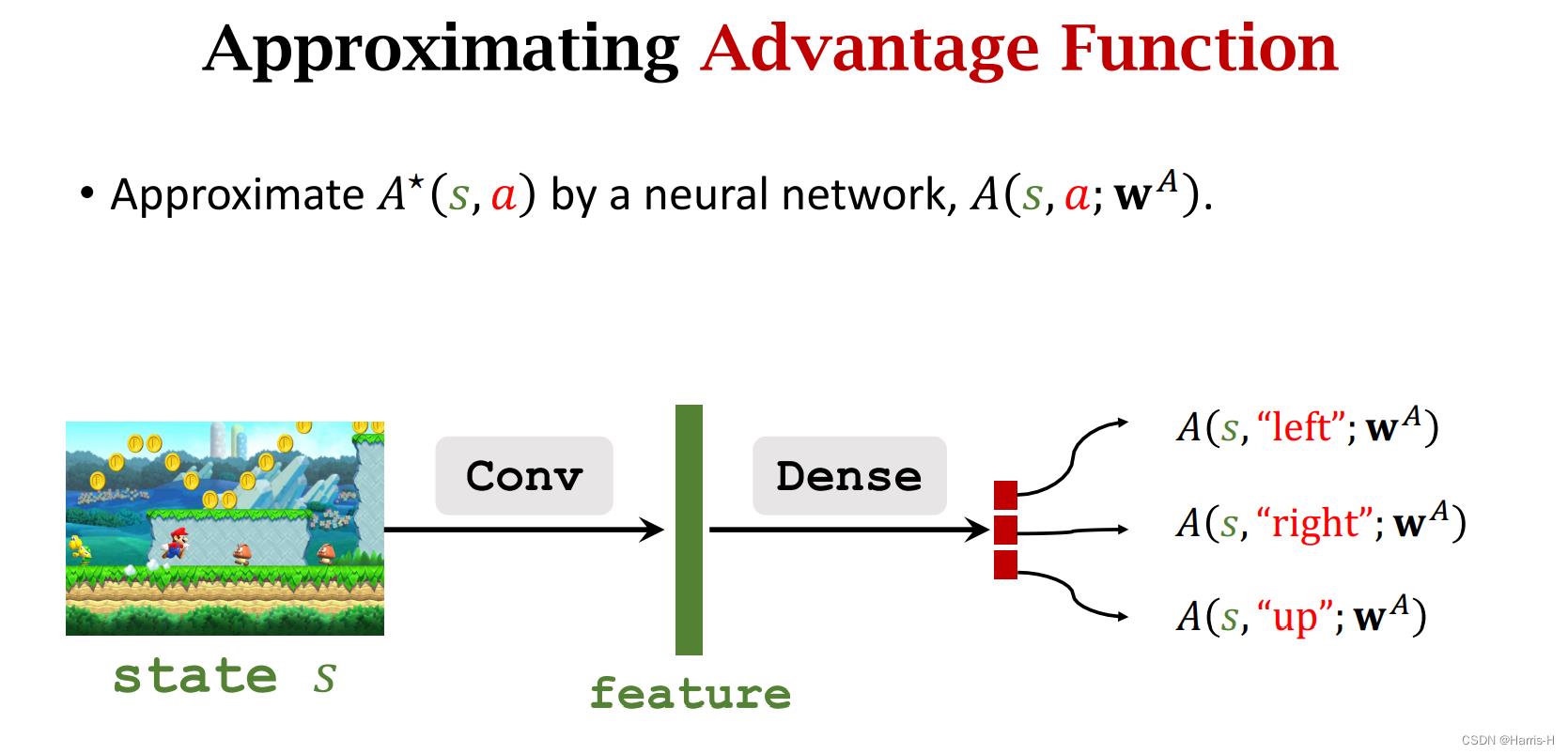
我们采用一个神经网络近似 A ∗ A^* A∗
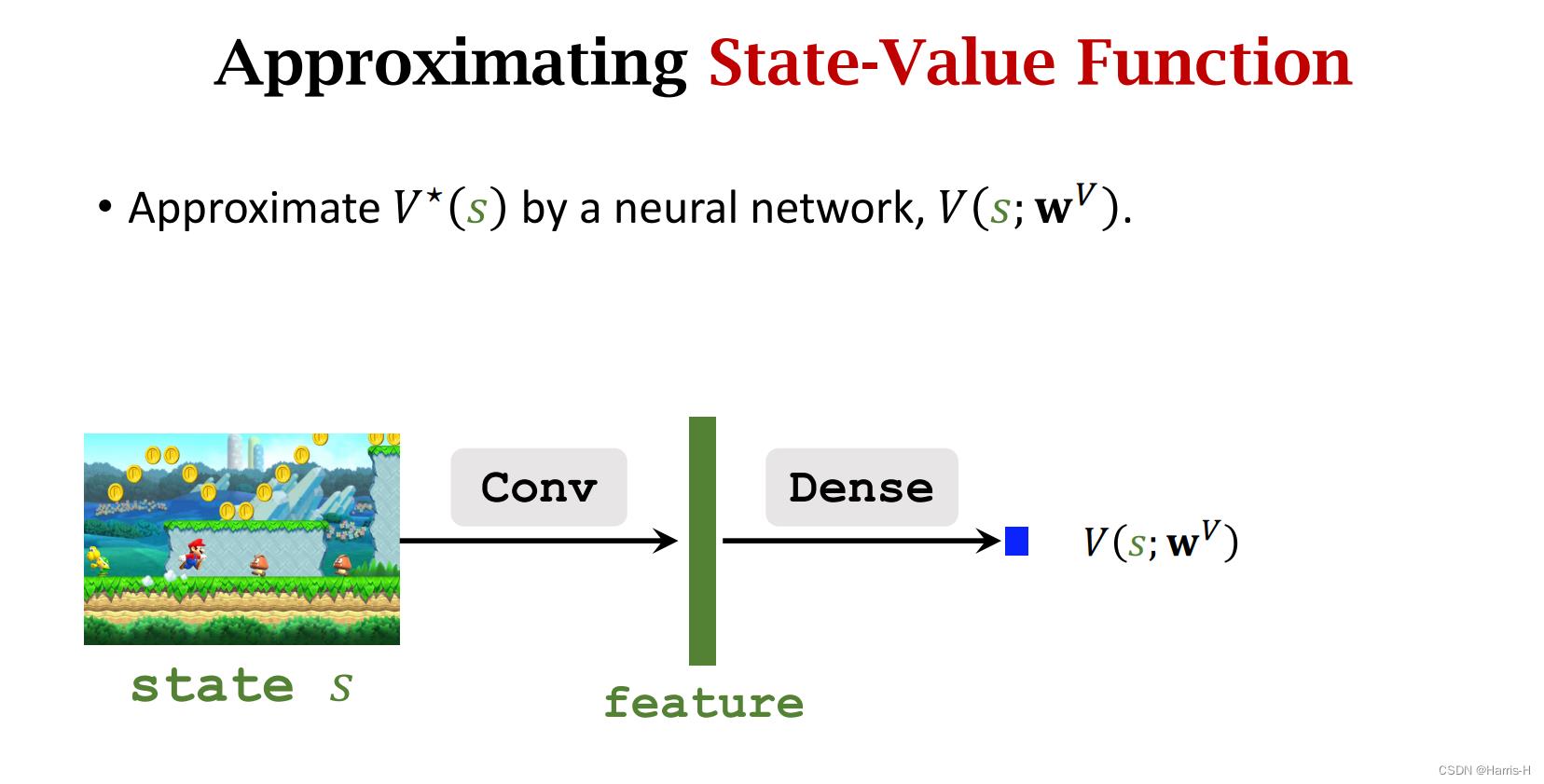
一个神经网络近似 V ∗ V^* V∗
3.2 网络模型
因此可以用这两个网络近似 Q ∗ Q^* Q∗


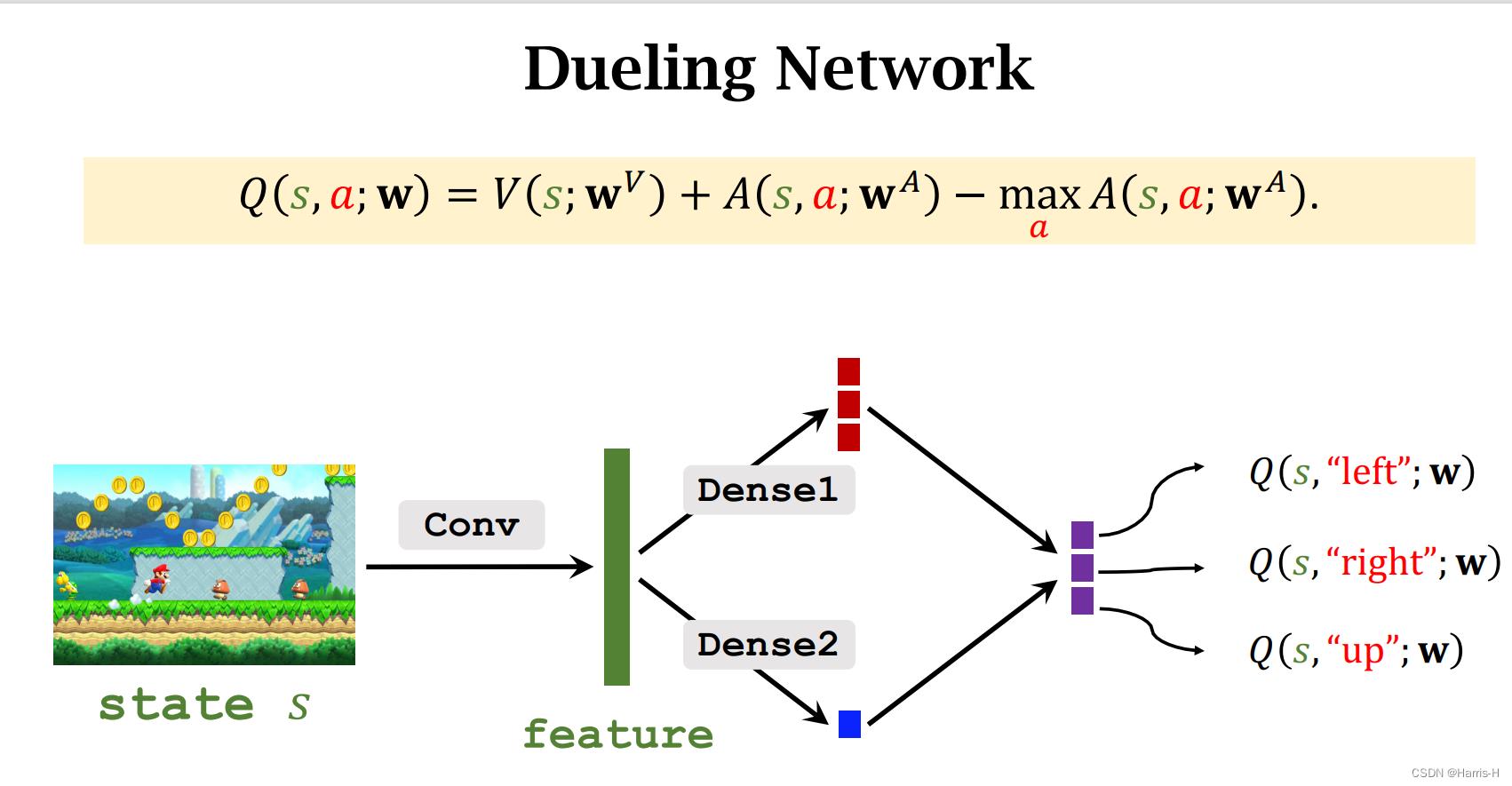
因为两个网络的卷积层操作相同,所以可以公用。

该网络同样可以使用experience replay、Double DQN,Multi-step TD 这些trick。
3.3 使用max-0常量的必要性


显然若 V ′ , A ′ V',A' V′,A′的变化和最后为0,其 Q Q Q 也不会影响。
但是会导致对 V V V, A A A的网络训练出现问题。

而引用max后就不会出现评价的偏差。
在实际应用中采用mean效果更优。

V , A V,A V,A 两者是一起训练的,参数看成一个整体 w = ( w V , w A ) w=(w^V,w^A) w=(wV,wA) ,训练方式与DQN类似。
以上是关于Optimization of DQN的主要内容,如果未能解决你的问题,请参考以下文章