基于PVO(Pixel-Value-Ordering)算法的高质量可逆隐藏方法和图像局部粗糙度分析

Posted 2022-09-26 fpga和matlab

目录

一、理论基础

二、MATLAB程序设计

三、测试结果

---

一、理论基础

    PVO算法，其首先将图像分为多个不重叠的块，每一个块的大小为N*N，然后在块内对N*N个像素点按其像素值大小进行排序，并根据像素的次最大值和次最小值的位置索引对信息进行隐藏嵌入。下面对其基本的原理进行介绍。

    假设某一个图像如下图所示：

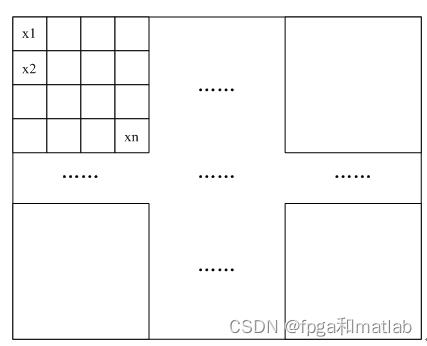
图1图像像块素示意图

 

 

表1次最大像素值预测最大像素值得到最大值预测误差的算例

图像块	原始图像	嵌入数据比特后图像	图像还原
图像块1	119  32    38    40 119  33    39    40 120  33    40    41 121 34    40    42	119  32    38    40 119  33    39    40 120  33    40    41 122 34    40    42	119  32    38    40 119  33    39    40 120  33    40    41 121 34    40    42
图像块2	34    34    36    38 35    34    35    37 33    33    34    36 32    31    33    35	34    34    36    39 35    34    35    37 33    33    34    36 32    31    33    35	34    34    36    38 35    34    35    37 33    33    34    36 32    31    33    35
图像块3	25    29   23    19 18    19    19    17 16    16    17    17 16    16    17    17	25    30   23    19 18    19    19    17 16    16    17    17 16    16    17    17	25    29   23    19 18    19    19    17 16    16    17    17 16    16    17    17

    从表1的结果可知，以第一个测试图像块为例子，其最大像素值和次大像素数值分别为121和120，b=1，那么嵌入之后，最大像素值变为122。通过提取b后，可以成功还原出原始图像。以上过程是基于次最大像素值预测最大像素值，并得到最大值预测误差的过程。

二、MATLAB程序设计

clc;
clear;
close all;
warning off;
addpath 'func\\'


 
I = imread(['images\\A\\1.jpg']);
[R,C,K]=size(I);
if K==3;
   Igray = rgb2gray(I); 
else
   Igray = I;  
end
Igray = imresize(Igray,[200,300]);
[R,C]=size(Igray);

figure
imshow(I);
title('热红外图像');
 
%%
%PVO算法
%图像分块
Igray  = double(Igray);
Kscale = 4;%定义分块大小
for i = 1:R/Kscale
    for j = 1:C/Kscale
        Ibki,j=Igray(Kscale*(i-1)+1:Kscale*i,Kscale*(j-1)+1:Kscale*j);
    end
end

%下面是单个块的PVO算法%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%对每一个块进行处理
%定义嵌入bit信息
b    = [1,1];
Is   = Ibk1,1;

%加入
Ijiam_max_pvo = func_pvomax_add(Is,b(1));           %用次最大值像素预测最大值像素
Ijiam_min_pvo = func_pvomin_add(Ijiam_max_pvo,b(2));%用次最小值预测最小值

Ijiam_min_pvo2= func_pvomin_get(Ijiam_min_pvo);
Ijiem_max_pvo = func_pvomax_get(Ijiam_min_pvo2);
%下面是整个图的PVO算法%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
b    = rand(1,100000)>=0.5;%随机产生需要隐藏的序列
idx  = 0;
%得到隐含信息后的图像
Ijiam= zeros(R,C);
isadd1=1;
isadd2=1;
for i = 1:R/Kscale
    for j = 1:C/Kscale
        idx  = idx+1;
        %定义嵌入bit信息
        bs   = b(2*(idx-1)+1:2*idx);
        Is   = Ibki,j;
        %加入
        [Ijiam_max_pvo,isadd1] = func_pvomax_add(Is,bs(1));            %用次最大值像素预测最大值像素isadd1用来判断是否加入假如隐含信号
        [Ijiam_min_pvo,isadd2] = func_pvomin_add(Ijiam_max_pvo,bs(2)); %用次最小值预测最小值

        [Ijiam_min_pvo2,b1]    = func_pvomin_get(Ijiam_min_pvo);
        [Ijiem_max_pvo, b2]    = func_pvomax_get(Ijiam_min_pvo2);
        
        Ijiam(Kscale*(i-1)+1:Kscale*i,Kscale*(j-1)+1:Kscale*j)=Ijiam_min_pvo;
        %提取隐含序列
        bget(2*(idx-1)+1:2*idx)=[b2,b1];
        
    end
end


figure
subplot(121);
imshow(Igray,[]);
title('原始图像');
subplot(122);
imshow(Ijiam,[]);
title('隐含信息后的图像');

%计算信号容量
idx = find(isnan(bget)==1);
bget(idx)=[];

length(bget)

clc;
clear;
close all;
warning off;
addpath 'func\\'


for i = 1:16
    i
    I = imread(['images\\A\\',num2str(i),'.jpg']);
    [R,C,K]=size(I);
    if K==3;
       Igray = rgb2gray(I); 
    else
       Igray = I;  
    end
    Igray = imresize(Igray,[200,300]);
    
    figure(1);
    subplot(121);
    imshow(I);
    title('热红外图像');
    %局部粗糙度
    [coarseness,coarseness0]= func_coarseness(Igray);
 
    subplot(122);
    imshow(coarseness,[]);
    title('粗糙度分布图');
    drawnow;
    Fccd(i)=mean2(coarseness0);
end
%统计分析
figure;
plot(Fccd);

save A.mat Fccd
% save B.mat Fccd
% save C.mat Fccd
% save normal.mat Fccd



figure;
imshow(I);
title('热红外图像');
 
figure;
imshow(coarseness,[]);
title('粗糙度分布图');
 

三、测试结果

       首先进行信息隐藏操作，分析其嵌入数据信息之后对应的图像质量。通过MATLAB仿真，我们可以得到信息嵌入容量以及峰值信噪比PSNR的仿真结果。

表1信息嵌入容量

样本数量	Tamura粗糙度定义算法			多层次Tamura粗糙度定义算法
	电气设备1	电气设备2	电气设备3	电气设备1	电气设备2	电气设备3
1	1780	879	1213	2153	1024	1537
2	1662	854	1340	2088	1038	1702
3	1406	946	1406	1769	1109	1778
4	1927	890	1359	2300	1015	1725
5	1934	914	1507	2282	1051	1786
6	1856	919	1531	2259	1084	1816
7	1959	929	1518	2311	1081	1779
8	1917	897	1533	2280	1048	1801
9	1893	847	1484	2214	997	1745
10	1985	961	1565	2364	1074	1803
11	1881	907	1515	2269	1036	1789
12	1847	991	1340	2281	1134	1702
13	1948	1034	1689	2358	1181	1986
14	1909	1013	1643	2362	1155	1937
15	1895	1032	1685	2318	1200	1999
16	1945	1070	1359	2362	1216	1725
均值	1859	943	1480	2248	1092	1788

    从表1的仿真结果可知，采用多层次Tamura粗糙度定义算法相对于传统的Tamura粗糙度定义算法，不同电气设备的热红外图像嵌入信息的容量提升了15%左右（如图3.2所示）。此外，通过对不同电气以及相同电气不同样本的嵌入容量可知，嵌入数据的容量一方面和图像的粗糙度分布有关，还和图像的分辨率有关。

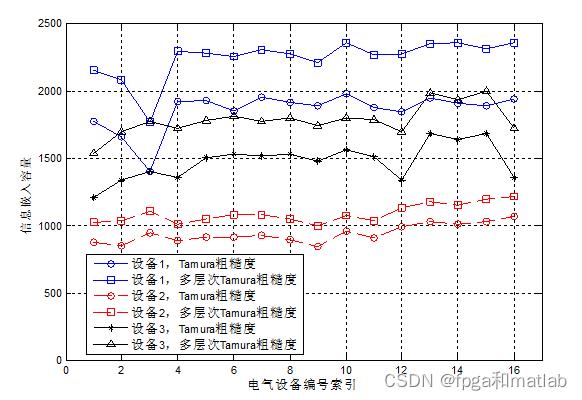
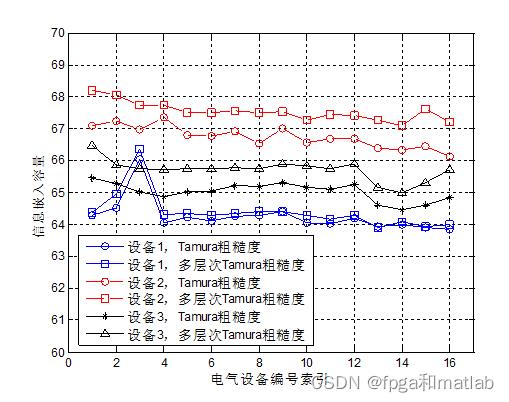
       采用多层次Tamura粗糙度定义算法相对于传统的Tamura粗糙度定义算法，其图像质量更高（如图3所示）。

 A09-60