ofdm_waveform_simplified_diagram_v0.4

Posted 2022-09-06 资质平庸的程序员

2016.07.30 – 07.31
[个人学习/探索笔记 —— 理解OFDM]

基带。信息源，也称发射端，发出的没有经过调制（进行频谱搬移和变换）的原始电信号所固有的频带（频率带宽）。
频带。对基带信号调制后所占用的频率带宽。
带宽。一个信号所占有的从最低的频率到最高的频率之差。
频谱搬移。频谱搬移是指在发射端将调制信号从低频端搬移到高频端， 便于天线发送或实现不同信号源，不同系统的频分复用。

1 OFDM数学描述

在复基带上的在时间段$mT_u \\le t \\le (m + 1)T_u$上的OFDM信号$x(t)$可由下式描述：

$$x(t) = \\sum_k = 0^N_c - 1x_k(t) = \\sum_k = 0 ^N_c - 1a_k^(m)e^j2 \\pi k \\Delta ft$$
[反正看不懂]

1.1 $e^j 2 \\pi k \\Delta ft$

可将该复指数理解为[2]中提到的随着时间$t$在复平面做螺旋线运动的波形（复频域），它可作为OFDM中的子载波（共$N_c$个），每个子载波的频率为$k \\Delta f$（k为第k个子载波，为子载波的序号， $\\Delta f$为各子载波的频率间隔）。因为它们具有正交性：

$$\\int_mT_u^(m + 1)T_ux_k_1x_k_2^*dt = \\int_mT_u^(m + 1)T_ua_k_1a_k_2^*e^j 2 \\pi (k_1 – k_2) \\Delta ftdt = 0, \\text for k_1 \\ne k_2$$

[从时域看]
从时域上看，该式子对应的是$cos(j 2 \\pi k \\Delta ft)$（欧拉公式，毫无我个人理解的根据），周期为$T_u$，开始于时间0。

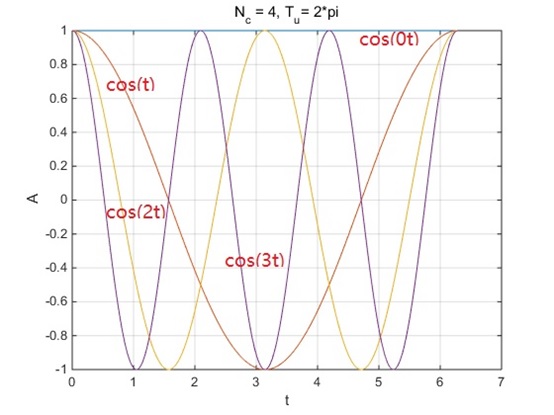
[从频域看]
时域的子载波相当于其在整个时域与一个周期为$T_u$、开始于0、幅值为1的矩形波相乘。时域乘法对应于频域卷积：整个时域上的余弦函数的频谱为一个冲激（如$cos(t)$的频率为$\\frac 1 T_u =\\frac12 \\pi$），矩形窗的频谱为sinc函数（$sinc(2 \\pi)$），两者卷积可得每子载波频谱（度婆卷积，然后可用笔算得到：sinc函数频谱搬移到冲激处）。

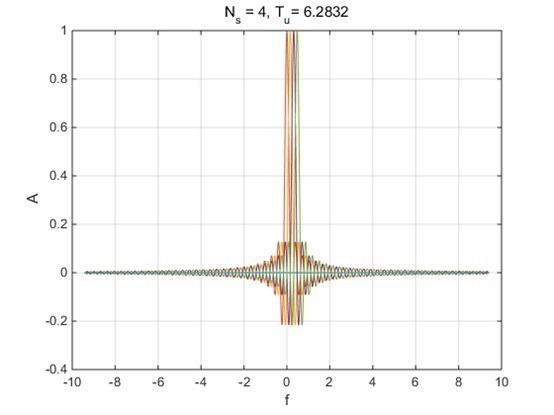
为了看得清楚，不与时域的周期一致，将周期缩小一倍后的子载波频率图如下。

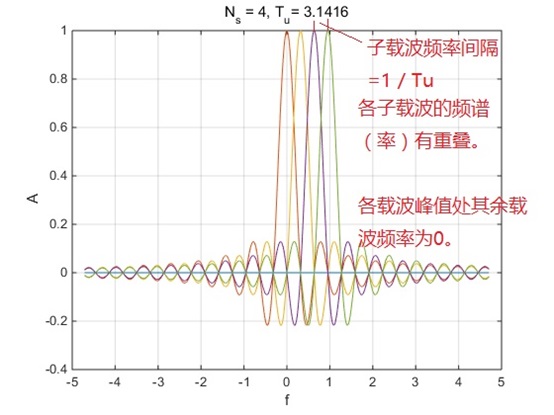
[请自动脑补傅里叶变换后得负频率 – 反正我还没脑补过来（唯有用螺旋线逆时针、顺时针旋转自圆其说）]

1.2 $a_k^(m)$

$a_k^(m)$代表PSK/QAM符号[参考OFDM符号ofdm_signal“1 映射”部分（挑对的看）]。

1.3 叠加

（子）载波：是一个特定频率的无线电波（某段频率内的波），是一种可用于传递（携带/表示）信息的波。
a(m)kej2πkTut $以上是关于ofdm_waveform_simplified_diagram_v0.4的主要内容，如果未能解决你的问题，请参考以下文章</p> <p > <a style="color:blue;" href="https://it.cha138.com/tech/show-257818.html">函数参数</a></p> <p > <a style="color:blue;" href="https://it.cha138.com/tech/show-432236.html">多重背包</a></p> <p > <a style="color:blue;" href="https://it.cha138.com/tech/show-751863.html">合租房合同模板</a></p> <p > <a style="color:blue;" href="https://it.cha138.com/tech/show-814362.html">启动代码分析 02</a></p> <p > <a style="color:blue;" href="https://it.cha138.com/tech/show-573370.html">ACM数论 求幂乘</a></p> <p > <a style="color:blue;" href="https://it.cha138.com/tech/show-640940.html">Windows下虚拟机安装Mac OS X &mdash;&ndash; VM12安装Mac OS X 10.11</a></p> </article> </div> </div> </div> </section> </div> </div> <script type="text/javascript" src="https://it.cha138.com/skin/m03sred/style/js/fixit.js">$