论文导读（AAAI) Unsupervised Causal Binary Concepts Discovery with VAEfor Black-Box Model Explanation

Posted 2022-09-06 ViviranZ

AAAI-2022上的新论文 读一读

【ABSTRACT】

目标：

解释一个黑盒分类器，其形式为：数据X被归类为Y类，因为X有A、B而没有C"，其中A、B和C是高级概念。挑战在于，我们必须以无监督的方式发现一组概念，即A、B和C，这对解释分类器是有用的。

实现方式：

我们首先介绍一个适合表达和发现这种概念的结构生成模型。然后我们提出一个学习过程，同时学习数据分布，并鼓励某些概念对分类器的输出有很大的因果影响。我们的方法还允许轻松整合用户的先验知识，以诱导概念的高可解释性。最后，利用多个数据集，我们证明了所提出的方法可以发现有用的概念来进行这种形式的解释。

【INTRODUCTION】

深度神经网络已被公认为是各种任务的先进模型。随着它们被应用于更多的实际应用中，人们逐渐达成共识，即这些模型需要是可解释的，特别是在高风险的领域。人们提出了各种方法来解决这个问题，包括建立一个具有可解释成分的模型和解释训练过的黑盒模型的事后方法（including building a model with interpretable components and post-hoc methods that explain trained black-box models）。我们专注于事后的方法，并提出一个新的基于因果概念的解释框架。

我们对符号解释感兴趣："数据X被归类为Y类，因为X有A、B而没有C"，其中A、B和C是高级概念。从语言学的角度来看，这样的解释是用名词和它们的部分-整体关系，即一个部分和整个物体之间的语义关系（such an explanation communicates using nouns and their part-whole relation）进行交流。在许多分类任务中，特别是图像分类，预测依赖于二元成分；例如，我们可以通过白色斑点的眼睛来区分熊猫和熊，或者通过斑马的条纹来区分斑马和马。这也是人类用来分类和组织知识的一种常见方式（Gardenfors 2014）。因此，这种形式的解释应该擅长于为分类器提供对人类友好的、有组织的见解，特别是对于涉及更高层次概念的任务，如检查黑盒模型与专家的一致性。从现在开始，我们把这样的概念称为二元概念。然而，我们也注意到，二元概念可能不足以代表具有连续域的有用概念，如颜色或长度。

我们的方法在解释中采用了三个不同的概念：因果二元开关、特定概念变体和全局变体（causal binary switches, concept-specific variants and global variants）。我们在图1中说明了这些概念。首先，因果二元开关和特定概念变体成对出现，代表不同的二元概念。特别是，因果二元开关控制着样本中每个二元概念的存在。交替使用这种开关，即在一个样本中删除或添加一个二元概念，会影响该样本的预测（例如，删除中间的笔画，将E变成C）。相比之下，特定概念的变体，其每一个都与特定的二元概念相联系，在一个二元概念中表达不同的变体，不影响预测（例如，改变中间笔画的长度不影响预测）。最后，全局变体，不与具体的二元概念相联系，表示不影响预测的其他变体（例如，偏斜度）。

我们的目标是发现一组二元概念，可以用它们的二元开关以无监督的方式解释分类器。与一些现有的工作类似，为了构建概念解释，我们学习一个生成模型，将每个输入映射到一个低维表示中，其中每个因素编码数据的一个方面。在实现我们的目标方面有三个主要挑战。

(1) 它需要一个充分的生成模型来表达二元概念，包括二元开关和每个概念中的变体。【充分性】

(2) 发现的二元概念必须对分类器的输出有很大的因果影响。我们要避免发现与预测相关但不导致预测的混杂概念。例如，天空概念经常出现在飞机的图像中，但可能不会导致飞机的预测。【必要性：不能取到spurious connection】

(3) 解释必须是可解释的，并提供有用的见解。例如，一个完全用字母A代替字母E的概念有很大的因果效应。然而，由于缺乏可解释性，这样的概念并不能提供有价值的知识。【难度较大】

在图2d和2e中，我们展示了所提出的方法对六个字母的分类器的解释。我们的方法成功地发现了底笔、中笔和右笔的概念（bottom stroke, middle stroke and right stroke），有效地解释了分类器。在图2d中，我们显示了编码的二进制开关和它们的干预结果。从上图中，我们可以解释：这个字母被归类为E，因为它有一个底笔画（否则就是F），一个中笔画（否则就是C），而且它没有右笔画（否则就是B）。我们还能够将每个概念中的变体（图2e顶部）与全局变体（图2e底部）区分开来。其他字母的完整结果与解释见实验部分。

就我们所知，没有任何现有的方法可以发现满足这些要求的二元概念。诸如Guided Backprop（Springenberg等人，2014）、Integrated Gradient（Sundararajan、Taly和Yan，2017）或GradCam（Selvaraju等人，2017）等显著性方法只显示特征的重要性，但没有解释原因（图2a）。一些使用二元连续混合潜势进行稀疏编码的生成模型，如VSC（Tonolini, Jensen, and Murray-Smith 2020）、IBP-VAE（Gyawali等人2019）、PatchVAE（Gupta, Singh, and Shrivastava 2020），可以支持二元概念。然而，它们不一定能发现在因果关系和可解释性方面对解释有用的二元概念（图2b）。最近，O'Shaughnessy等人（2020）提出了一个学习框架，鼓励某些潜在因素对分类器输出的因果影响，以学习对预测有因果关系的潜在表示。然而，他们的模型不能拆分二元概念，而且很难解释，特别是对于多类任务。例如，一个单一的概念将字母E变为其他多个字母（图2c），这将不会对这个潜变量如何影响预测做出任何解释。我们的工作有以下贡献。
- 我们引入了发现解释的二元概念的问题。然后，我们提出了一个构建二元概念解释的结构生成模型，它可以捕获二元开关、特定概念变体和全局变体。【引入问题+构造模型】
- 我们提出了一个学习过程，以同时学习数据分布，同时鼓励二元开关的因果影响。尽管VAE模型通常鼓励各因素的独立性，以实现有意义的拆分，但这样的假设对于发现有用的因果概念是不够的，这些概念往往是相互关联的。我们的学习过程，考虑了二元概念之间的依赖性，可以发现具有更显著因果关系的概念。【实现拆分+抵抗依赖性】
- 为了避免具有因果关系但没有可解释性的概念，所提出的方法允许以一种简单的方式实现用户的偏好和先验知识作为正则器，以诱导概念的高可解释性。【简单+高可解释性】
- 最后，我们证明我们的方法成功地发现了对解释任务有用的具有因果关系的可解释二元概念。

【Related Work】

 我们的方法可以归类为基于概念的方法，利用数据的高层方面进行解释。概念的定义是多种多样的，例如，激活空间中的一个方向（Kim等人，2018；Ghorbani等人，2019），一个原型的激活向量（Yeh等人，2020）或生成模型的一个潜在因素（O'Shaughnessy等人，2020；Goyal等人，2020）。我们注意到，这个概念应该取决于数据和解释目标。一些作品使用额外的数据事先定义了概念，并专注于评估这些概念。当这种侧面信息没有得到时，人们需要为解释发现有用的概念（discover useful concepts for the explanation,），例如，Ghorbani等人（2019）使用分割和聚类，Yeh等人（2020）用原型概念层重新训练分类器，O'Shaughnessy等人（2020）用因果目标学习生成模型。【在图像中举例，低层次原信息为图像的RGB数据，高层次是纹理、皮毛、金属等概念（神经网络层数较高的地方出现的信息），这段里提到之前的工作有旨在研究高层次特征进行解释，但是还有不足：1、需要额外数据先验确认的概念特征（获得侧面信息） 2、额外进行定义以实现可解释】

像VAE这样的生成模型可以提供一个基于概念的解释，因为它学习了一个捕捉数据的不同方面的潜在呈现z。然而，Locatello等人（2019年）表明，如果没有归纳偏见，以完全无监督的方式进行分解表征从根本上是不可能的。一种流行的方法是用正则器增强VAE损失（Higgins等人，2017；Burgess等人，2018）。另一种方法是将结构纳入表示中（Choi, Hwang, and Kang 2020; Ross and Doshi-Velez 2021; Tonolini, Jensen, and Murray-Smith 2020; Gupta, Singh, and Shrivastava 2020）。虽然这些方法可以鼓励分解和稀疏表征，但学到的表征不一定可以解释，对分类器输出有因果关系。

我们追求有因果关系的解释。因果性的解释是有帮助的，因为它可以避免只与预测相关但不导致预测的归因和概念。以前的工作曾试图以各种方式关注因果关系。例如，Schwab和Karlen（2019）采用格兰杰因果关系来量化输入特征的因果效应，Parafita和Vitria（2019）评估了具有先验已知因果结构的潜在归因的因果关系（evaluated the causality of latent attributions with a prior known causal structure），Narendra等人（2018）评估了网络层的因果效应，Kim和Bastani（2019）学习了具有因果保证的可解释性模型。一些工作首先训练生成模型，然后在潜在空间上搜索反事实样本（Joshi等人，2019；Dhurandhar等人，2018）。虽然这些方法可以为每个输入样本提供一个反事实的解释，但他们的生成模型不一定能分解出有用的概念。一些工作将因果结构引入生成模型（Yang等人，2020；Kocaoglu等人，2017）。这些方法不适用于我们的环境，因为它们需要额外的知识，例如，因果图或概念标签。就我们所知，没有任何现有的工作可以使用满足我们三个要求的概念来解释。

【Preliminaries】

Variational Autoencoder……

我们的解释是建立在Kingma和Welling（2014）提出的VAE框架之上。VAE模型假设了一个数据的生成过程，其中潜伏的Z首先从先验分布p(z)采样，然后通过条件分布p(x | z)生成数据。通常情况下，由于难以处理，会引入难以处理的后验的变异近似值q(z | x)，然后使用证据下限（ELBO）学习模型，即

 这里，q(z | x)是将数据映射到潜在空间的编码器，p(x | z)是将潜在空间映射到数据空间的解码器。通常，q(z | x)和p(x | z)分别被参数化为中性网络Q(z | x)和G(x | z)。q(z | x)的常见选择是因子化的高斯编码器q(z | x) = QP p=1 N (µi , σ2 i ) 其中(µ1, . . , µP , σ1, . . , σP , ) = Q(x)。p(z)的常见选择是多变量正态分布N(0, I)，均值为零，协变量为同一。假设xˆ是输入x的重构，VAE目标可以写成如下，并通过重新参数化技巧进行优化。【具体细节可看VAE的论文】

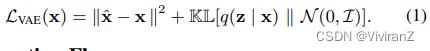
信息流 

接下来，我们介绍我们用来量化所学表征对分类器输出的因果影响的措施。我们采用Information Flow，它使用Pearl的do calculus（Pearl 2009）来定义因果强度。给定一个因果定向无环图G，信息流使用干预分布的条件互信息来量化统计影响。

定义1（有向无环图G中从U到V的信息流（Ay and Polani 2008））。设U和V是不相交的节点子集。从U到V的信息流I（U→V）定义为

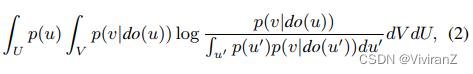
 其中do(u)代表因果模型中的干预，将u固定为一个值，而不考虑其父辈的值。

 O'Shaughnessy等人（2020）认为，与其他指标如平均因果效应（ACE）（Holland 1988）、方差分析（ANOVA）（Lewontin 1974）相比，信息流更适合于捕捉变量之间复杂和非线性的因果关系

 【proposed method】

我们的目的是发现一组二元概念M = m_0, m_1，…， m_M具有因果关系和可解释性，可以解释黑盒分类器f: X→Y。受O’shaughnessy et al.(2020)的启发，我们使用生成模型来学习数据分布，同时鼓励某些潜在因素的因果影响。特别地，我们假设在图3a中有一个因果图，其中每个样本x是由一组潜在变量生成的，包括二元概念的M对和一个概念特定的变量γi， αi^M_i=1，以及一个全局变量β。当我们想要使用二进制开关γi来解释分类器输出(即图3a中的节点y)时，我们预计γi对y有很大的因果影响。

我们提出的学习目标由三个组成部分组成，这对应于我们的三个要求:VAE目标LCE(x)用于学习数据分布p(x)，因果效应目标LCE(x)用于鼓励γi对分类器输出y的因果影响，以及一个用户可实现的正则化LR(x)用于提高所发现概念的可解释性和一致性:

 VAE Model with Binary Concepts

为了表示二元概念，我们采用了一个结构，其中每个二元概念mi由一个潜变量ψi表示，它由两个因素进一步控制：一个二元概念转换潜变量γi（简称概念转换）和一个代表特定概念变体的连续潜变量αi（简称特定概念变体），即

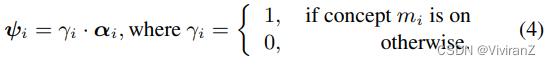
这里，概念开关γi控制概念mi是否在样本中被激活，例如，控制图像中是否出现底部笔画（图2d）。另一方面，特定概念的变体αi控制概念mi中的变体，例如，底部笔画的长度（图2e，顶部）。除了影响仅限于特定二元概念的概念特定变体αi外，我们还允许一个全局变体latent β来捕捉其他不一定有因果影响的变体，如偏斜度（图2e，下）。在这里，将特定概念的变体和全局变体分开是很重要的，因为它可以帮助用户理解所发现的二元概念。【奇奇怪怪的，加了一个01的值控制要不要关注这个父节点】

 我们表示二元概念的方式与钉板分布（spike-and-slab distribution）密切相关，它被用于贝叶斯变量选择(George和McCulloch 1997)和稀疏编码(Tonolini, Jensen和Murray-Smith 2020)。与这些模型不同，我们的模型只使用少量的二进制概念和一个多维全局变量β。我们的直觉是，分类很可能是通过组合少量的二进制概念来进行的。

【输入编码】假设A = (α1, α2, ..., αM)，我们使用网络Q^d (x)和Q^c (x)分别对离散成分q(γ | x)和连续成分q(A, β | x)的变异后验分布进行参数化 

这里，我们对连续潜质采用了δ-移折正态分布(δ-Shifted Folded Normal Distribution) N^fold_δ (µ, σ2 )，它是|x| + δ的分布，有一个恒定的超参数δ > 0，其中x ∼ N (µ, σ2 )。在我们所有的实验中，我们采用δ=0.5。我们没有选择标准的正态分布，而是选择了δ-移动的折叠正态分布，因为它更适合于我们想要实现的因果效应。我们在扩展版本中详细讨论了这种设计选择及其功效（Tran等人，2021）。

【输出解码】接下来，给定q(γ | x)和q(A, β | x)，我们首先分别从它们的后验中抽出概念开关 ˆdi、概念变体αˆ i和全局变体β。利用这些抽样的潜质，我们使用公式（4）中的二元概念机制构建一个聚合表示zˆ=（ψ1, ... , ψM, βˆ），其中ψi是概念mi的对应部分，即ψi=γi×αi。也就是说，如果概念mi是开着的，我们让ˆdi=1，这样ψi就能反映出特定概念的变体αˆi。否则，当概念mi关闭时，我们让ˆdi=0。 我们把zˆ称为概念潜伏代码。最后，解码器网络将zˆ作为输入，生成重构的xˆ作为

【学习过程】我们使用证据下限最大化（ELBO）来联合训练编码器和解码器。我们假设连续潜势的先验分布是δ-移折正态分布N^fold_δ (0, I)，具有零均值和相同协方差。此外，我们假设二进制潜质的先验分布是具有先验π_prior的Bernoulli分布Bern(π_prior)。我们的学习过程的ELBO可以写成：

第一个项可以用L2重建损失来训练，而其他KL-分歧项则用重参数化技巧来训练。对于伯努利分布，我们在训练过程中使用其连续近似值，即放松的伯努利（Maddison, Mnih, and Teh 2017）。

 Encouraging Causal Effect of Binary Switches

 我们希望二元开关γ有很大的因果影响，以便它们能有效地解释分类器。为了测量γ对分类器输出Y的因果影响，我们采用了图3a中的因果DAG，并采用信息流（定义1）作为因果测量。我们的DAG采用了一个与标准VAE模型根本不同的假设。具体来说，标准的VAE模型和O'Shaughnessy等人（2020）假设潜伏因素是独立的，这被认为是鼓励通过因素化的先验分布进行有意义的分解。我们声称，由于有用的解释概念往往在因果上取决于类信息，因此并不相互独立，这样的假设可能不足以发现有价值的因果概念。例如，在字母E中，中间和底部的笔画与字母E的识别有因果关系，而相应的二元概念是相互关联的。因此，采用VAE的因子化先验分布来估计信息流可能会导致很大的估计误差，并妨碍发现有价值的因果概念。

相反，我们采用先验分布p∗（γ），允许因果二元概念之间存在相关性。我们的方法迭代学习VAE模型，并使用当前的VAE模型来估计最有可能产生用户数据集的先验分布p ∗ (γ)，然后用p ∗ (γ)来评估公式（3）中的因果目标。假设X是一组来自p(x)的i.i.d样本，我们估计p ∗ (γ)为

 在最后一行，p(γ | x)被替换成VAE模型的变异后验q(γ | x)。这里，因子化的变异后验q(γ | x)只假设以每个样本为条件的潜变量之间的独立性，但并不意味着p∗ (γ)中二元开关的独立性。我们注意到，在这里我们的目的不是学习概念之间的依赖性，而只是期望p∗（γ）正确反映数据集X中出现的二元概念之间的依赖性，以便更好地评估因果效应。我们将通过实验证明，使用p ∗ (γ)的估计会对数据集X的因果效应进行更好的估计，并为解释提供更有价值的概念。

由于我们想使I(γ → Y)最大化，我们将其改写为损失项LCE = -I(γ → Y)，并与VAE模型的学习一起优化。我们还表明，在拟议的DAG中，信息流I(γ → Y )与相互信息I(γ; Y )重合。
命题1（拟议的DAG中信息流和相互信息的重合(Coincident of Information Flow and Mutual Information in proposed DAG).）。在图3a的DAG中，从γ到Y的信息流与γ和Y之间的相互信息相吻合。就是说

证明和估计I(γ; Y)的详细算法在我们的扩展版本中描述（Tran等人，2021）。 

 Integrating User Preference for Concepts

最后，我们讨论了用户的偏好或先验知识对于诱导概念的高可解释性的必要性。使用深度生成模型发现有意义的潜在因素的一个问题是，学到的因素可能很难解释。尽管因果关系是密切相关的，并且可以促进可解释性，但由于深层模型的高表达性，大的因果效应并不总是保证可解释的概念。例如，一个完全用字母D替换字母E的概念将大大影响预测结果。然而，它并没有提供有价值的知识，也很难解释。为了避免这样的概念，我们允许用户将他们的偏好或先验知识作为可解释的规范器来实施，以限制生成模型的表达能力。我们的方法在受限的搜索空间下寻找具有大因果关系的有用的二元概念。

整合可以很容易地通过一个评分函数r(x_γi=0, x_γi=1)来完成，该函数评估了概念mi的有用程度。这里，x_γi=0和x_γi=1是通过对输入x分别执行do-operation do(γi=0)和do(γi=1)从生成模型中得到的。在这项研究中，我们引入了两个基于以下直觉的正则器。首先，一个可解释的概念应该只影响少量的输入特征（公式（11））。这个要求是通用的，可以应用于许多任务。第二条是更具体的任务，我们把重点放在灰度图像分类任务上。一个概念的干预应该只增加或减少像素值，而不是同时增加或减少（公式（12））。此外，我们希望γi=1表示有像素存在，γi=0表示没有像素存在。我们将这些正则器表述如下

其中M是概念的数量，P是输入的维度，xˆ[i]是反转概念mi的潜伏代码γˆi后的重建。我们对公式（12）做一个简单的解释。考虑样本x中的概念mi。如果概念mi被激活，即γˆi=1，那么xˆ[i]对应于关闭干预do（γi=0）。在这种情况下，我们期望这种干预只删除xˆ中的一些像素。因此，对于像素值增加的位置p，即xˆ [i] p>xˆp>xˆp>xˆp的位置，我们对差值|xˆp - xˆ [i] p>进行惩罚。最后，我们将这些正则器合并为

使用这些可解释性正则器，我们观察到发现的二元概念的可解释性有了明显的改善。

实验

EMNIST(Cohen et al. 2017), MNIST(Lecun et al. 1998) and Fashion-MNIST

 对于每个数据集，我们选择几个类，并对所选类进行分类器训练。特别是，我们为EMNIST选择了字母 "A、B、C、D、E、F"，为MNIST选择了数字 "1、4、7、9"，为Fashion-MNIST数据集选择了 "t-shirt/top、dress、coat"。我们注意到，我们的设置比现有作品中常见的测试设置（例如，MNIST 3和8位数的分类器）更具挑战性，因为分类任务中涉及到更多的类和概念。由于篇幅所限，这里我们主要展示对EMNIST数据集的视觉解释，其中我们使用了M=3个概念。αi和β的维度分别为K=1和L=7。其他数据集的解释结果和进一步的详细实验设置可以在我们的扩展版本中找到（Tran等人，2021）。 

在图5中，我们展示了EMNIST数据集的三个被发现的二进制概念。在每幅图像中，我们在第一行显示了不同样本的概念mi的编码二进制转换，其中黄色表示γˆi = 1，灰色表示γˆi = 0。第二行显示了原始的重建图像xˆ，而第四行显示了当我们扭转二进制转换xˆ [i]时重建的图像。边框颜色表示每个图像的预测结果。最后，第三行显示xˆ和xˆ[i]的差异。

从图5中，我们观察到，所提出的方法能够发现有用的二进制概念来解释分类器。首先，这些概念的二进制开关对分类器的输出有很大的因果影响，即交替开关会影响预测结果。例如，图5a解释了在字母A上加一个底线对分类器的输出有很大影响。每个概念都捕获了一组类似的干预，可以很容易地解释，即概念m0代表底部笔画，概念m1代表右侧笔画，而概念m2代表内部（中间）笔画。

图5中的解释可以被认为是一种局部解释，侧重于解释特定的样本。不仅如此，所提出的方法在提供关于所发现的概念和预测类的有组织的知识方面也很出色。特别是，我们可以汇总图5中每个概念和类别的因果效应，以评估每个二进制开关是如何改变预测的。使用do操作do(γi = d)(d∈0, 1)，可以得到一个概念mi从y = u到y = v的过渡概率为

其中Xu = x∈X | f(xˆ) = u。在图6中，我们将每个概念的计算出的过渡概率显示为一个图，其中每个音符代表一个预测类。实线箭头（虚线箭头）代表激活（停用）一个概念时的过渡，箭头的厚度显示过渡概率w do(γi=1) u,v (w do(γi=0) u,v )。我们忽略了过渡概率小于0.1的过渡。例如，从图6a中可以看出，底部的笔画对于区分（E,F）和（A,B）非常重要。

最后，在图4（a,b,c）中，我们显示了每个概念中被捕获的变体和其他对分类器输出有小影响的全局变体。与二进制开关相比，这些变体解释了不改变预测的内容。我们首先使用dooperation do(γi = 1)激活概念mi，然后在交替使用αi时绘制重建图。我们观察到，α0捕获了底部笔画的长度，α1捕获了右侧笔画的形状，而α2则分别捕获了内部（中间）笔画的长度。特别是，我们的方法还能够将特定概念的变体与其他全局变体β如偏斜度、高度或宽度区分开来（图4 d,e）。

 5.3 Comparing with other method

我们将我们的方法与图2中显示的其他基线进行比较。首先，基于显著性地图的方法，使用显著性地图来量化（超级）像素的重要性，虽然很容易理解，但并没有解释为什么突出的（超级）像素很重要（图2a）。因为他们只为每个输入提供了一种解释，他们不能解释这些像素如何将预测的类别与其他类别区分开来。我们的方法，有多个概念，可以进行不同的干预，以获得多种解释。

接下来，我们与O'Shaughnessy等人（2020）进行比较，在该模型中，我们使用了一个具有10个连续因素的VAE模型，并鼓励三个因素对预知的类有因果效应。在图7中，我们将取得最大因果效应的α0可视化。在图7a（7b）中，我们减少（in- crease）α0，直到其预测标签发生变化，并在第三行显示该干预结果。首先，我们观察到，由于α0影响了所有的底层、中层和右层笔画，它未能分离出不同的因果因素。例如，在图7a中，减少αt使第10列的字母D变成了字母B（中笔画概念），而使第11列的字母D变成了字母C（左笔画概念）。在图7b中也观察到类似的结果，即让位给E。其次，它未能分离出特定概念的变体，这并不影响预测。例如，对于图7b中的字母A和B（第1至第6列），增加α0不仅影响中间笔画的出现，而且还改变了右边笔画的形状。

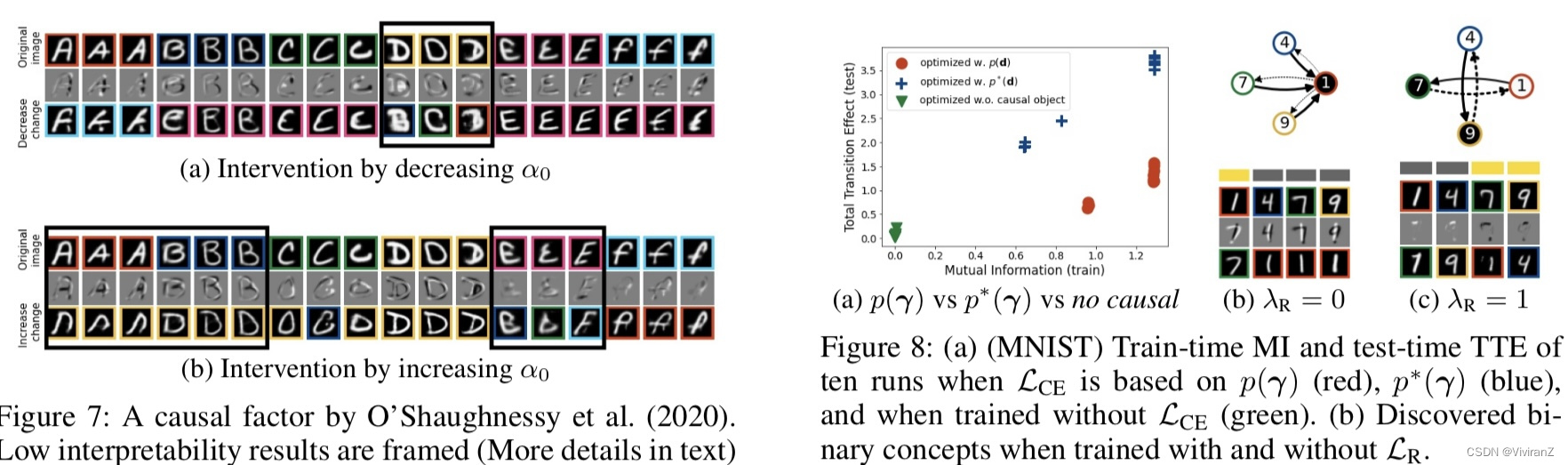
 我们的方法通过精心设计的二元离散结构，加上所提出的因果效应和可解释性正则器，克服了这些限制。通过对二进制开关的因果影响的考虑，我们的方法可以将影响预测的因素和具有相同预测的样本的变体分开。因此，它能使一个二进制开关mi只把预测从一个类yk变成另一个类yk′，从而得到一个更可解释的解释。我们还强调，仅靠二元连续的混合结构还不足以获得有价值的解释概念（图2b）。

5.4 Quantitative results

我们使用总转换效应（TTE）来评估一个概念集的因果影响，其定义为

其中M和T分别是概念和类的数量。这里，TTE的数值越大，表明整个发现的概念集对所有类的转换具有显著的整体因果效应。与信息流相比，TTE可以更直接、更忠实地评估数据集X上的二元转换的因果效应，而且，它也更容易被终端用户理解。

在图8a中，我们显示了当因果目标LCE使用先验p∗(γ)（公式(9)）、VAE模型的先验p(γ)和没有LCE训练时的测试时间相互信息和TTE值。在所有设置中都包含了可解释性正则器。我们观察到，当使用p(γ)时，有些情况下，估计的相互信息很高，但总的过渡效应却很小。另一方面，用估计的p∗（γ）得到的相互信息与TTE值更一致。我们声称这是由于p(γ )与 "真实 "的p∗ (γ )之间的偏差造成的。通过对运行中的p∗ (γ )进行估计，我们的方法可以更好地评估和优化γ对y的因果影响。此外，我们还观察到，如果没有因果目标，我们就不能发现因果二元概念。

接下来，我们评估了通过LR实现用户的偏好和先验知识如何增加概念的可解释性。在图8b中，我们展示了当我们在没有可解释性正则器的情况下训练模型时，所涵盖的概念的一个例子。我们看到，交替使用这个概念的二进制开关（顶部）只是用数字1替换了数字4、7、9，但并没有提供任何适当的解释，为什么这个图像被识别为1。我们的方法，使用可解释性正则器，可以发现具有高可解释性的二元概念，充分解释数字7可以根据顶部笔画的出现而与数字1区分开来（图8c）。原则上，如果我们能在其他数据域上训练生成模型的话，该方法也可以应用于该域。然而，对于一个更复杂的领域来说，获得可解释的概念可能更具挑战性。作为未来的工作，我们计划探索更具挑战性的任务，例如，医学图像分类和其他领域，如文本或表格数据。

Conclusion

我们介绍了发现解释黑盒分类器的二元概念的问题。

我们首先提出了一个能够正确表达二元概念的结构生成模型。

然后，我们提出了一个学习过程，该过程同时学习数据分布，并鼓励二进制开关对分类器输出有很大的因果影响。所提出的方法还允许整合用户的偏好和先验知识，以获得更好的可解释性和一致性。

我们证明了所提出的方法可以发现具有较大因果效应的可解释的二元概念，这可以有效地解释多个数据集的分类模型。