算法小讲堂之二叉排序树|二叉搜索树|BST

Posted 2022-08-31 MangataTS

一、定义

二叉排序树（也称二叉查找树）或者是一棵空树，或者是具有下列特性的二叉树：

• 若左子树非空，则左子树上所有结点的值均小于根结点的值。
• 若右子树非空， 则右子树上所有结点的值均大于根结点的值
• 左、右子树也分别是一棵二叉排序树。

对于二叉树的每一个结点，我们可以有两种不同的定义方式，当然后面的操作也是分为两种：

• 其一（主要用于考研书籍）

typedef struct Node
	ElemType data;
	struct Node *lchild, *rchild;
Node;

• 其二（用于竞赛代码）

struct Node
    int val,ls,rs,cnt;//分别表示的是结点的值、左儿子、右儿子、结点出现的次数
tree[500010];

二、 查找操作

如果我们想查找某个值的元素是否存在在树中，我们可以从根节点的元素进行比较，然后我们将查找元素和根节点进行比较，如果根节点和查找元相等的话那么就找到了，如果查找元素比根节点大的话我们就往右子树走，否则往左子树走，直到找到了就返回找到的结点

• case1

Node *BST_Search(Node *root,ElemType key) 
    while(root != NULL && root->data != key) 
        if(root->data < key) root = root->rchild;
        else root = root->lchild;
    
    return root;

• case2

int find(int x,int v)//x是当前查询位置的下标，v是查询的值

	while(x != 0 && tree[x].val != v) 
		if(tree[x].val < v) x = tree[x].ls;//往左走
		else x = tree[x].rs;//往右走
	
	if(tree[x].cnt == 0) x = -1;
	return x;

三、插入操作

插入操作其实和查找类似，我们从根节点开始不断与之比较，最后找到一个空结点的位置，当然如果在查找的过程中找到了这个元素，那么说明插入失败，因为已经存在了

• case1

Node * Create_Node(ElemType key) 
    Node *p = (Node)malloc(sizeof(Node));
    p->data = key;
    p->lchild = p->rchild = NULL;


int BST_insert(Node *root,ElemType key) 
    if(!root) //如果是根节点元素为空的话
        root = Create_Node(key);
        return 1;
    
    if(root->data == key)
        return 0;//已经存在，插入失败
    else if(root->data < key) //插入到右子树
    	if(root->rchild == NULL) 
            Node *p = Create_Node(key);
            root->rchild = p;
            return 1;//成功插入
         else 
            return BST_insert(root->rchild,key);
        
    
    else //插入到左子树
    	if(root->lchild == NULL) 
            Node *p = Create_Node(key);
            root->lchild = p;
            return 1;//成功插入
         else 
            return BST_insert(root->lchild,key);
        
    

• case2

void add(int x,int v)//x是当前查询位置的下标，v是插入的值

    if(tree[x].val==v)
        //如果恰好有重复的数，就把cnt++，退出即可，因为我们要满足第四条性质
        tree[x].cnt++;
        return ;
    
    if(tree[x].val>v)//如果v<tree[x].val，说明v实在x的左子树里
        if(tree[x].ls!=0)
          add(tree[x].ls,v);//如果x有左子树，就去x的左子树
        else//如果不是，v就是x的左子树的权值
            cont++;//cont是目前BST一共有几个节点
            tree[cont].val=v;
            tree[x].ls=cont;
        
    
    else//右子树同理
        if(tree[x].rs!=0)
          add(tree[x].rs,v);
        else
            cont++;
            tree[cont].val=v;
            tree[x].rs=cont;
        
    

四、构造操作

不断将序列中的元素加入到二叉树即可

• case1

Node *Create_BST(Node *root,ElemType vec[],int n) 
    root = NULL;
    for(int i = 0;i < n; ++i) 
        BST_insert(root,vec[i]);
    
    return root;

• case2

int Create_BST(int root,vector<int> vec,int n) 
    root = 1;
    for(int i = 0;i < n; ++i) 
        add(root,vec[i]);
    
    return root;

五、删除操作

关于删除操作因为考虑到删除的结点不一定都是叶结点，于是我们需要对删除的结点进行分类讨论：

• ①若被删除结点 $z$ 是叶结点，则直接删除，不会破坏二叉排序树的性质
• ②若结点 $z$ 只有一棵左子树或右子树，则让 $z$ 的子树成为 $z$ 父结点的子树，替代 $z$ 的位置
• ③若结点 $z$ 有左、右两棵子树， 则令 $z$ 的直接后继（或直接前驱）替代 $z$ ，然后从二叉排序树中删去这个直接后继（或直接前驱），这样就转换成了第一或第二种情况

下图则是三种不同情况的删除操作绘图：

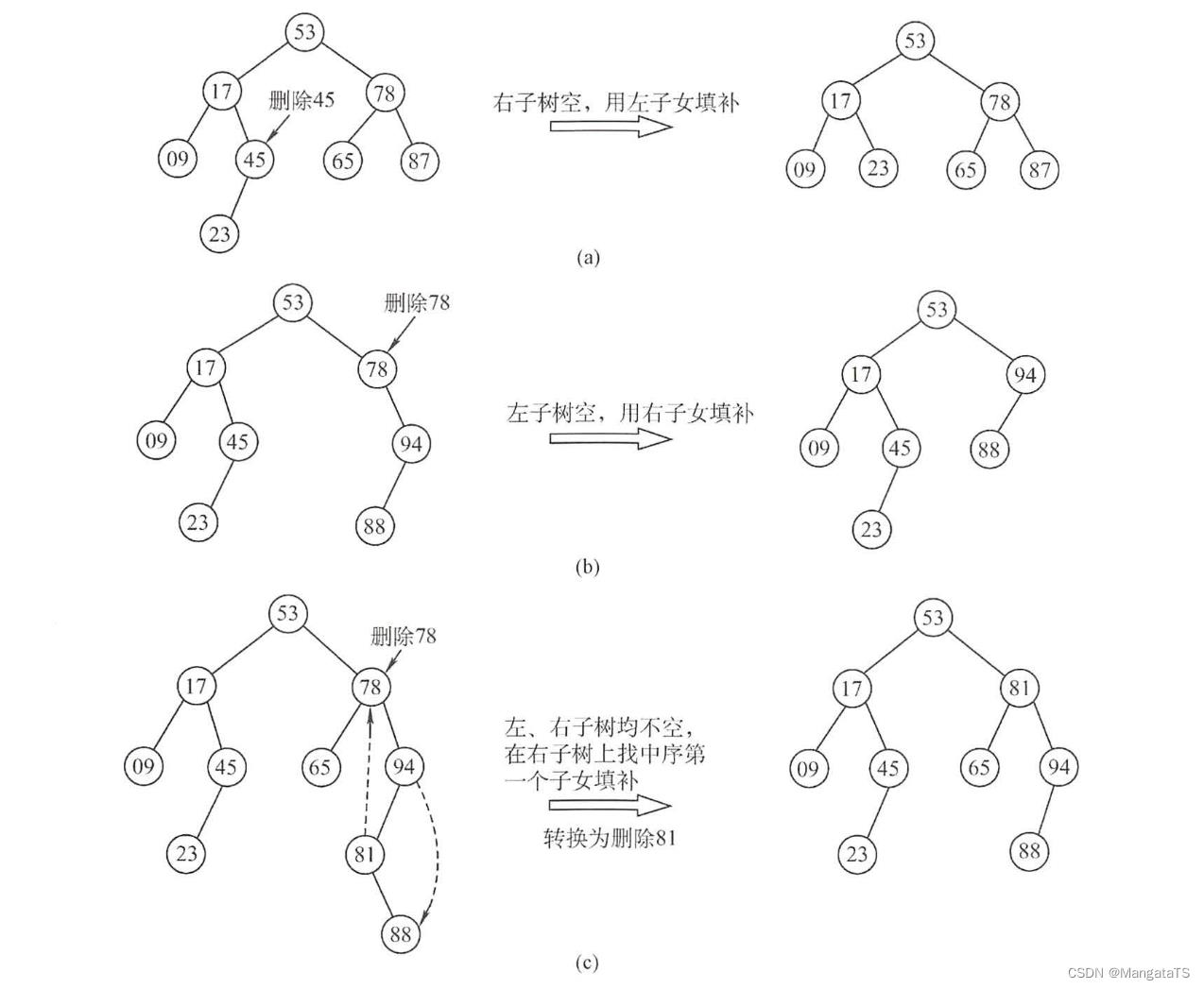
删除操作的话，如果是通过第二种写法只需要找到相关结点并且将其 cnt 减一即可，如果是第一种写法则会麻烦很多，需要三种情况的判断，我这里就不给出代码了，重点是删除的思想，掌握即可

六、效率分析

效率取决于二叉树的高度。

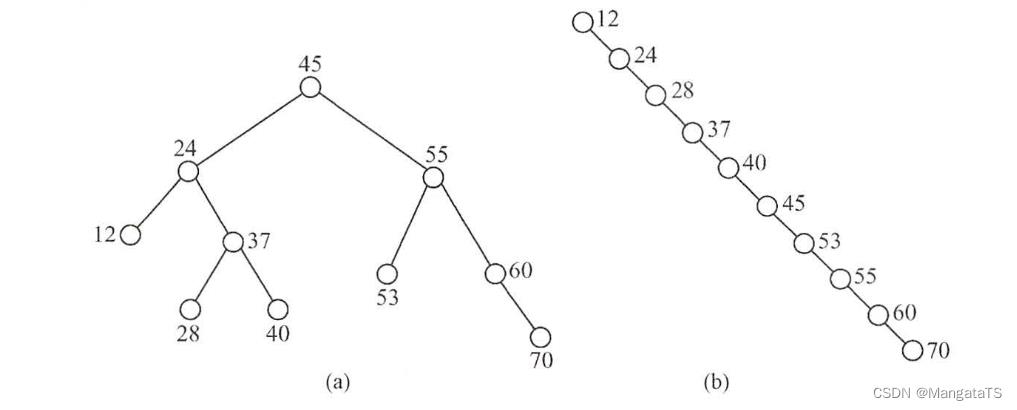
最坏效率：二叉树退化成链，复杂度为 $O(N)$

一般效率：二叉树的左右子树高度差的绝对值不超过 $1$ ，这样的树其实就是后面提到的平衡二叉树，他的平均查找复杂度为 $O(lo{g}_{2}n)$

从查找过程看， 二叉排序树与二分查找相似。 就平均时间性能而言， 二叉排序树上的查找和二分查找差不多 。 但二分查找的判定树唯一，而二叉排序树的查找不唯一，相同的关键字其插入顺序不同可能生成不同的二叉排序树 ，如下图所示