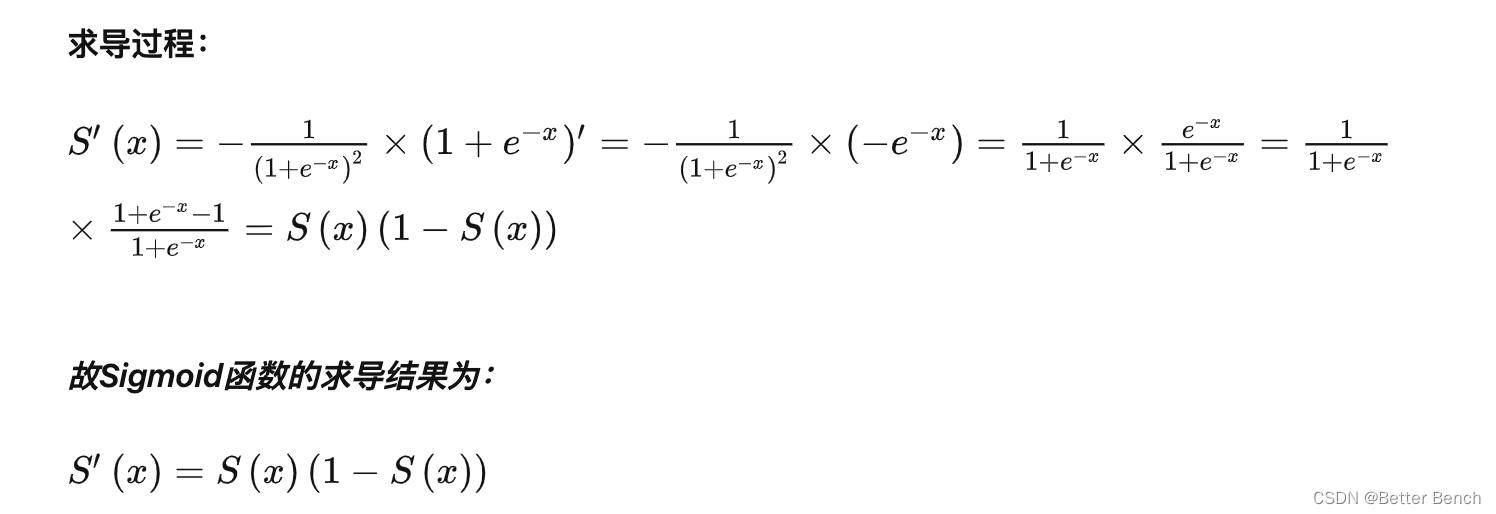数据挖掘2022年昆仑万维 算法工程师笔试题

Posted 2022-08-29 Better Bench

【数据挖掘】2022年昆仑万维 算法工程师笔试题

企业：昆仑万维

1 单选题

1、ABCDE，出栈的顺序不可能是？

栈的知识

2、连续投硬币，第一次正面，奇数次A赢，偶数次B赢。则A赢的概率是多少

问题转化：
该问题相当于A，B轮流投硬币，先出正面就赢。

假设A赢的概率为p，则

p+0.5p=1，结果为p=2/3

3、Label = [0,0,0,1,1]，predict= [0.1,0.4,0.6,0.5,0.8]，求AUC 等于多少？

ACU 的计算公式
$$AUC=\frac{{\sum }_{i=1}^{M}ran{k}_i正样本-\frac{M(M+1)}{2}}{M\times N}$$
M是正样本个数，N是负样本的个数，rank是根据概率排序正样本的序号，从1开始编号

0.1 （序号1，负样本）、0.4（序号2，负样本）、0.5（序号3，正样本），0.6（序号4，负样本），0.8（序号5，正样本）

则
$$AUC=\frac{3+5-\frac{2(2+1)}{2}}{2\times 3}=\frac{5}{6}$$

4、ALex网络中矩阵是227×227×3，卷积核是11×11×3，步长stride = 4,padding=2，则卷积后的矩阵大小是多少？

O=输出图像的尺寸。

I=输入图像的尺寸。

K=卷积层的核尺寸

N=核数量

S=移动步长

P =填充数

输出图像尺寸的计算公式如下：
$$O=\frac{I-K+2P}{S}+1$$
则 O=（ 227-11+2×2）/4+1 = 56

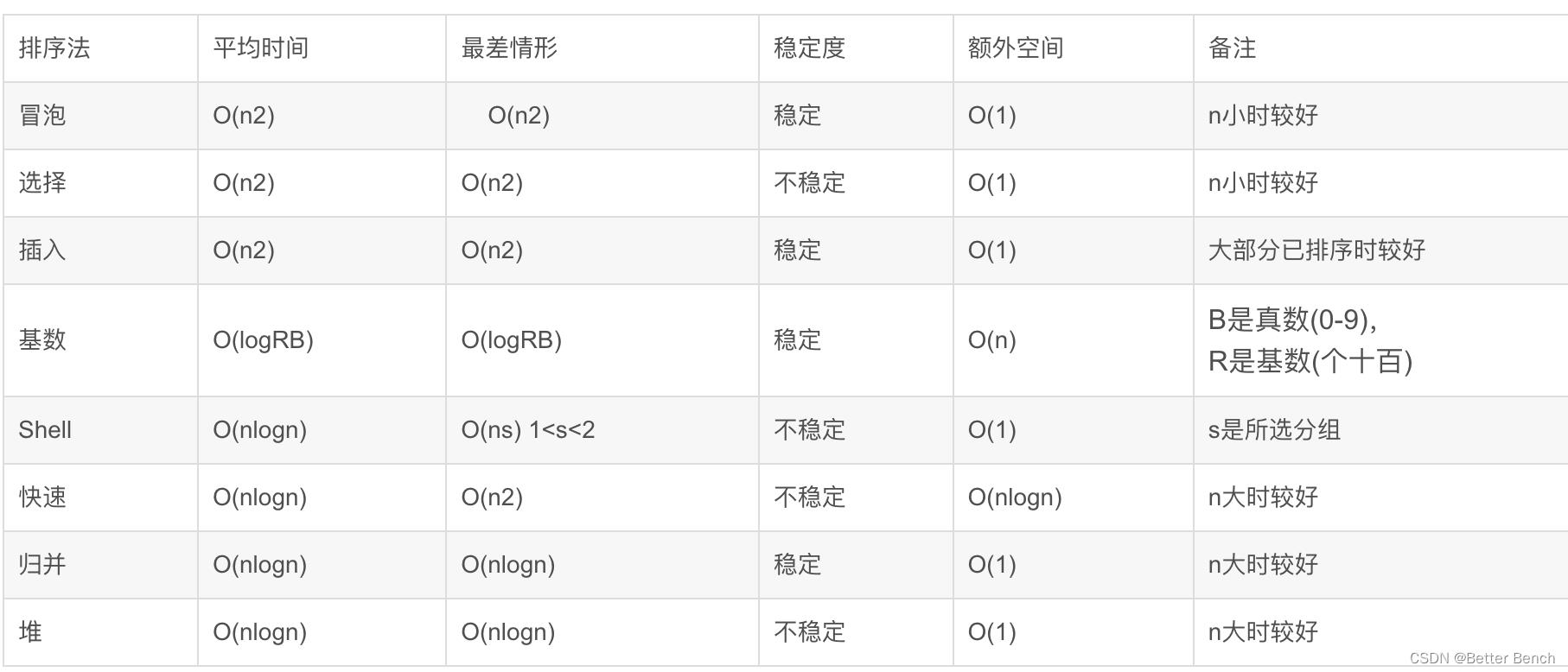
5、在排序算法中，最坏情况下的时间复杂度时O(NLogN)的算法是？

答案：归并排序

6、sigmoid函数S(x)的导数是什么？用f(z)表示

S’(x) = S(x)(1-S(x))

7、矩阵A、B 、C，大小分别是m×n，n×p，p×q，m<n<p<q，则效率最高的乘法顺序是什么？

考查矩阵相乘的效率问题，即需要计算的乘法和加法的次数之和。当m,n,p,q较大时，加法忽略不计。任意两个大小分别为a×b,b×c的矩阵相乘，需要乘法的次数为a×b×c

乘法顺序只有(AB)C和A(BC)

第一个选项的乘法计算次数，m×n×p+m×p×q；第二个选项的乘法计算次数，n×p×q+m×n×q

举例来计算大小，设m=1,n=2,p=3,q= 4

则m×n×p+m×p×q = 18，n×p×q+m×n×q = 32

8、8个信箱，一个信封，放在8个中任意一个信箱中的概率是4/5，不放的概率是1/5，第一个信箱为空，则7个信箱中会有这个信封的概率是多少？

答案：未知，我猜是$1-(0.2{)}^7$

9、30瓶药水，一瓶变质了，小老鼠喝了以后一个小时后会死去，那一个小时内至少多少个老鼠可以判断出药水是哪瓶？

用二进制来表示这个问题，则30瓶药水，需要30位二进制来表示30种情况，则$2^4<30<2^5$，则需要5只老鼠才够。

10、50个红球，50个篮球，任意组合方式放入到两个盒子中，之后随机从任意一个中拿出一球，它是红球的最大概率是？

一个红球放在一个箱子里，其余求全部放到另一个箱子。

这样放的概率为：0.5+0.5*(49/99) 约等于0.75（74/99）

此时取到红球的概率最大。

2 多选题

1、Batch Nornalization 的作用和本质？

D、BN通过减少内部协变量来加速深度网络训练

解析：BN就是通过归一化手段，将每层输入强行拉回均值0方差为1的标准正态分布，这样使得激活输入值分布在非线性函数梯度敏感区域，从而避免梯度消失问题，大大加快训练速度。

D选项是正确的，由于在训练期间，每一层的输入分布随着前一层参数的改变而发生改变，故训练深度神经网络是复杂的。需求低的学习率与谨慎的参数初始化令训练速度变慢，并且训练饱和非线性模型十分困难。我们称这种现象为内部协变量偏移，并且使用归一化层解决这个问题。BN减少内部协变量偏移以加速深度网络训练

2、激活函数的特性？

A、 非线性

B、具有饱和区

C、几乎处处可微

D、计算简单

答案：A、C、D

（1）非线性：即导数不是常数。这个条件前面很多答主都提到了，是多层神经网络的基础，保证多层网络不退化成单层线性网络。这也是激活函数的意义所在。

（2）几乎处处可微：可微性保证了在优化中梯度的可计算性。传统的激活函数如sigmoid等满足处处可微。对于分段线性函数比如ReLU，只满足几乎处处可微（即仅在有限个点处不可微）。对于SGD算法来说，由于几乎不可能收敛到梯度接近零的位置，有限的不可微点对于优化结果不会有很大影响[1]。

（3）计算简单：正如题主所说，非线性函数有很多。极端的说，一个多层神经网络也可以作为一个非线性函数，类似于Network In Network[2]中把它当做卷积操作的做法。但激活函数在神经网络前向的计算次数与神经元的个数成正比，因此简单的非线性函数自然更适合用作激活函数。这也是ReLU之流比其它使用Exp等操作的激活函数更受欢迎的其中一个原因。

（4）非饱和性（saturation）：饱和指的是在某些区间梯度接近于零（即梯度消失），使得参数无法继续更新的问题。最经典的例子是Sigmoid，它的导数在x为比较大的正值和比较小的负值时都会接近于0。更极端的例子是阶跃函数，由于它在几乎所有位置的梯度都为0，因此处处饱和，无法作为激活函数。ReLU在x>0时导数恒为1，因此对于再大的正值也不会饱和。但同时对于x<0，其梯度恒为0，这时候它也会出现饱和的现象（在这种情况下通常称为dying ReLU）。Leaky ReLU[3]和PReLU[4]的提出正是为了解决这一问题。非饱和激活函数可以解决梯度消失问题；非饱和激活函数可以加速收敛。

（5）单调性（monotonic）：即导数符号不变。这个性质大部分激活函数都有，除了诸如sin、cos等。个人理解，单调性使得在激活函数处的梯度方向不会经常改变，从而让训练更容易收敛。

（6）输出范围有限：有限的输出范围使得网络对于一些比较大的输入也会比较稳定，这也是为什么早期的激活函数都以此类函数为主，如Sigmoid、TanH。但这导致了前面提到的梯度消失问题，而且强行让每一层的输出限制到固定范围会限制其表达能力。因此现在这类函数仅用于某些需要特定输出范围的场合，比如概率输出（此时loss函数中的log操作能够抵消其梯度消失的影响[1]）、LSTM里的gate函数。

（7）接近恒等变换（identity）：即约等于x。这样的好处是使得输出的幅值不会随着深度的增加而发生显著的增加，从而使网络更为稳定，同时梯度也能够更容易地回传。这个与非线性是有点矛盾的，因此激活函数基本只是部分满足这个条件，比如TanH只在原点附近有线性区（在原点为0且在原点的导数为1），而ReLU只在x>0时为线性。这个性质也让初始化参数范围的推导更为简单[5][4]。额外提一句，这种恒等变换的性质也被其他一些网络结构设计所借鉴，比如CNN中的ResNet[6]和RNN中的LSTM。

（8）参数少：大部分激活函数都是没有参数的。像PReLU带单个参数会略微增加网络的大小。还有一个例外是Maxout[7]，尽管本身没有参数，但在同样输出通道数下k路Maxout需要的输入通道数是其它函数的k倍，这意味着神经元数目也需要变为k倍；但如果不考虑维持输出通道数的情况下，该激活函数又能将参数个数减少为原来的k倍。

（9）归一化（normalization）：这个是最近才出来的概念，对应的激活函数是SELU[8]，主要思想是使样本分布自动归一化到零均值、单位方差的分布，从而稳定训练。在这之前，这种归一化的思想也被用于网络结构的设计，比如Batch Normalization[9]。

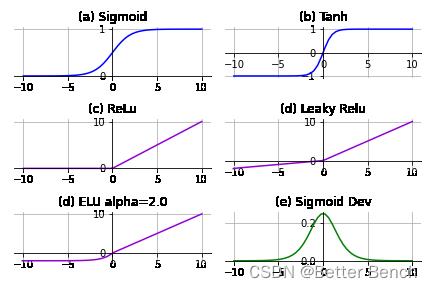
3、Sigmoid、Tanh、Relu、Leak Relu激活函数的公式和图像？

4、降低过拟合问题的方法？

A、数据扩增

B、正则化数据

C、降低架构复杂度

D、增加更多数据

答案：A、B、C、D

5、闰月和时间问题？

A、 8月有30天

B、7天有31天

C、3月有31天

D、2014年2月有28天

1、3、5、7、8、10、腊，三十 一天永不差

3 编程题

1、LeetCode：309. 最佳买卖股票时机含冷冻期（python）
给定一个整数数组，其中第 i 个元素代表了第 i 天的股票价格 。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
示例:

输入: [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

class Solution:
    def maxProfit(self, prices):
        if not prices:
            return 0
        # 初始化状态
        dp_i_0, dp_i_1 = 0, float('-inf')
        # 初始化前 2 天未持有股票状态的收益
        dp_pre_0 = 0           
        # 等同于 i=0 处开始迭代
        for i in range(len(prices)):
            # 记录前 1 天状态
            temp = dp_i_0
            # 更新当天状态
            dp_i_0 = max(dp_i_0, dp_i_1+prices[i])
            dp_i_1 = max(dp_i_1, dp_pre_0-prices[i])
            # 更新记录的前 1 天状态为前 2 天状态
            dp_pre_0 = temp
        return dp_i_0

https://blog.csdn.net/qq_36512295/article/details/100915460

2、剑指 Offer II 082. 含有重复元素集合的组合
题目描述：

给定一个可能有重复数字的整数数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次，解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

提示:

1 <= candidates.length <= 100
1 <= candidates[i] <= 50
1 <= target <= 30

def combinationSum(candidates, target) :
    # write code here
    ans = []
    candidates.sort()
    n = len(candidates)
    def dfs(idx,res):
        if sum(res)>target:
            return 
        if sum(res)==target:
            ans.append(res[:])
            return 
        for i in range(idx,n):
            if i>idx and candidates[i]==candidates[i-1]:# 去重复
                continue
            res.append(candidates[i])
            dfs(i+1,res)
            res.pop()
    dfs(0,[])
    return ans