差分数组(定义+性质+证明+代码实现+巩固练习)

Posted 2022-08-24 白龙码~

文章目录

• 差分数组
• • 一、定义
  • 二、利用差分数组恢复原数组
  • 三、差分数组的应用：区间快速加减
  • 四、巩固练习
  • • **描述**
    • **示例**
    • **思路分析**
    • 代码实现

差分数组

一、定义

差分数组本质就是一个与原数组大小相同的数组，记原数组为arr，差分数组为d，则：

1. i等于0时，d[i]=arr[i]；
2. i大于0时，d[i]=arr[i]-arr[i-1]，即原数组对应下标的元素与前一个元素的差。

---

二、利用差分数组恢复原数组

• i等于0时，arr[i]=d[i]；

• i大于0时:
  $$\begin{gathered} \because d[0]=arr[0] \\ d[1]=arr[1]-arr[0] \\ ... \\ d[i-1]=arr[i-1]-arr[i-2] \\ d[i]=arr[i]-arr[i-1] \\ \therefore arr[i]=d[0]+d[1]+...+d[i]=arr[i-1]+d[i] \end{gathered}$$

即：arr[i]为差分数组d[0...i]的前缀和，亦即arr[i-1]+d[i]。

---

三、差分数组的应用：区间快速加减

对区间[start, end]统一加上x(x∈R)，只需要对d[start]+x, d[end+1]-x

以数组[1, 2, 2, 4, -3, 6]举例：

对区间[1, 4]统一加**-3**，则：

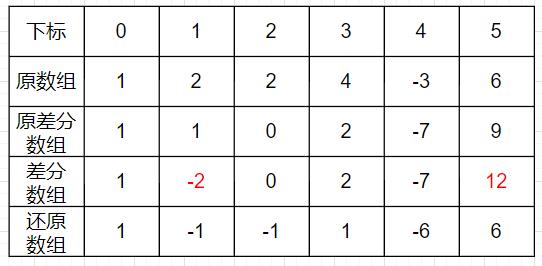
证明：
$$\begin{gathered} 对arr[start...end]+=x \\ \because d[start]=arr[start]-arr[start-1] \\ arr[start]+=x，arr[start-1]不变 \\ \therefore d[start]+=x \\ 又\because d[end+1]=arr[end+1]-arr[end] \\ arr[end]+=x，arr[end+1]不变 \\ \therefore d[end+1]-=x \\ 而对于d[start+\mathrm{1...}end]，我们以d[start+1]为例： \\ \because d[start+1]=arr[start+1]-arr[start] \\ arr[start+1]+=x,arr[start]+=x\therefore d[start+1]保持不变 \\ 对于d[start+\mathrm{2...}end]，可以同理得到证明 \end{gathered}$$
因此，当我们需要对一个很大的区间进行统一的加减时，利用差分数组只需要修改两个下标值即可完成该工作。

---

四、巩固练习

题目出自LeetCode 1109.航班预订统计

描述

这里有 n 个航班，它们分别从 1 到 n 进行编号。

有一份航班预订表 bookings，表中第 i 条预订记录 bookings[i] = [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti（包含 firsti 和 lasti ）的每个航班上预订了seatsi个座位。

请你返回一个长度为 n 的数组 answer，里面的元素是每个航班预定的座位总数。

示例

输入：bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5
输出：[10,55,45,25,25]
解释：
航班编号 1 2 3 4 5
预订记录 1 ：10 10
预订记录 2 ： 20 20
预订记录 3 ： 25 25 25 25
总座位数： 10 55 45 25 25
因此，answer = [10,55,45,25,25]

思路分析

bookings[i] = [firsti, lasti, seatsi]，意味着给航班编号为[firsti, last]统一加上座位数seatsi，这就是差分数组的典型应用：区间快速加减。

由于每个航班初始座位为0，因此原数组arr每个元素为0，即差分数组每个元素为0。

通过遍历bookings数组，对差分数组进行加减，最后通过差分数组还原arr即可！

代码实现

vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) 

    vector<int> d(n + 2, 0); // 多开空间，方便编号到数组下标的直接映射

    for (auto booking : bookings)
    
 		// 为区间：[ booking[0], booking[1] ] 增值booking[2]
        // 只需要修改差分数组的booking[0]和booking[1]+1
        d[booking[0]] += booking[2];
        d[booking[1] + 1] -= booking[2];
       

    vector<int> res(n); // 结果数组长度必须为n，因此下标i映射航班i+1
    for (int i = 0; i < n; ++i)
    
        if (i == 0)
        
            res[i] = d[i + 1];
        
        else
        
            res[i] = res[i - 1] + d[i + 1];
        
    

    return res;