逻辑回归原理梳理_以python为工具 Python机器学习系列

Posted 2022-08-18 侯小啾

逻辑回归原理梳理_以python为工具 【Python机器学习系列（九）】

文章目录

• 1.传统线性回归
• 2.引入sigmoid函数并复合
• 3. 代价函数
• 4.似然函数也可以
• 5. python梯度下降实现逻辑回归
• 6.python梯度下降实现非线性逻辑回归

---

---

大家好，我是侯小啾！

 今天分享的内容是，逻辑回归的原理，及过程中的公式推导。并使用python实现梯度下降法的逻辑回归。
    ʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞ

---

1.传统线性回归

逻辑回归是一种常用的回归模型，是广义的线性回归的一种特例。做线性回归时，我们采用预测函数的一般形式为：

              $h(X)={\omega }^{T}X+b={\theta }^{T}X$

（其中$b$可以和$\omega$和并写为$\theta$，这样即相当于给矩阵X一个全为1的列。）

---

2.引入sigmoid函数并复合

在使用逻辑回归做分类问题时，单纯的这个式子已经不能满足我们的需求。以二分类为例，样本数据中对事件是否发生的描述，只有0和1。为建立描述目标事件发生概率与样本特征之间的关系，因为事件发生的概率分布在[0,1]区间内，所以这里可以与sigmoid函数组成复合函数：
 
          $g(z)=\frac{1}{1+e^{-z}}$

---

sigmoid函数的定义域为全体实数，而值域为(0,1)，函数曲线如图所示：
      

---

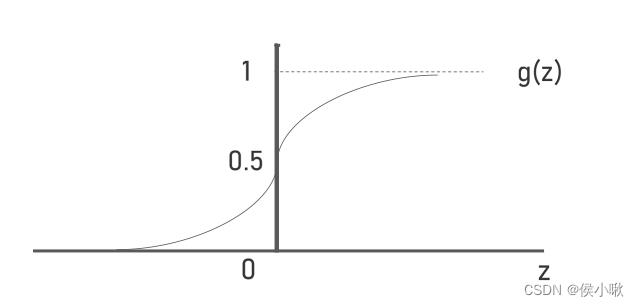
将h(x)嵌套进g(z)得到新的H(x)表达式为：
 
     $H(X)=g(h(X))=p=\frac{1}{1+e^{-({\omega }^{T}X+b)}}$

这里的H(X)表示事件发生概率的的预测值 p。（即结果为1的概率，值越大表示结果越可能为1，越小表示结果越可能为0）

---

此式，也等价于将对数几率$\ln \frac{p}{1-p}$ 对 X 做回归：
 
         $\ln \frac{p}{1-p}={\omega }^{T}X+b$

（这里只做普及，下边进一步的过程还使用H(x)而不用对数几率。因为以样本结果的1和0作为真实的p值，取值只有0和1，而当p=1时的对数几率为无穷，所以不适用。）

---

3. 代价函数

在传统的线性回归中，我们只需找到能使均方误差最小的$\omega$和$b$值即可，这个表示均方误差的表达式即“代价函数”。在这里的逻辑回归中，我们同样需要选择合适的代价函数：

$cost(H(X),y_i)=-\frac{1}{m}{\sum }_{i=1}^m[-y_i(\ln (H(X))-(1-y)\ln (1-H(X)))]$

其中，m表示样本总数为m。如何理解这个式子呢：
 
因为H(X)是在(0,1)范围内的，所以$\ln (H(X))$是负数，在前边再加负号即为正值，取值范围为大于0的全体实数。
$-y_i(\ln (H(X))$ 和 $-(1-y)\ln (1-H(X)))$两个式子总是有一个为0。
 
当$y_i$为1时，$-y_i(\ln (H(X))$不为0，该式子越大，则表示预测错误的越严重，越小则表示预测的越准确；同理，$-(1-y)\ln (1-H(X)))$式子则表示$y_i=0$的时候，预测的的准确性（也是越大越不准确）。所以我们需要找到能使得$cost(H(X),y_i)$最小 的$\omega$和$b$值。

这个式子还可以进一步化简，具体这里不再展示。

---

4.似然函数也可以

也可以使用似然函数代替代价函数：

      $L(\omega )={\prod }_{i=1}^m{p}^{y_i}(1-p{)}^{1-y_i}$

此表达式的含义是，每个样本预测正确的概率的乘积。
其中p即H(X)预测的结果。$y_i$的取值可以是1和0，所以当$y_i$为1时$(1-p{)}^{1-y_i}$为1，而$y_i$为0时$p^{y_i}$为1。
而我们的目的是，尽可能地使得这个乘积最大。

对该表达式两边同时去对数，得：

$l(\omega )={\sum }_{i=1}^m(y_i\ln p+(1-y_i)\ln (1-p))$
 
   $={\sum }_{i=1}^m(y_i{\omega }^T{x}_i-\ln (1+e^{<}$