动态规划 ＜ 第 3 天 ＞

Posted 2022-08-12 一朵花花

题目

• • 1.求路径总数
  • • 分析
    • 代码实现：
  • 2.最小路径和
  • • 分析
    • 代码实现：

1.求路径总数

题目：
一个机器人在 m×n 大小的地图的左上角（起点）
机器人每次可以向下或向右移动。机器人要到达地图的右下角（终点）
可以有多少种不同的路径从起点走到终点 ？
.
备注：m 和 n 小于等于100,并保证计算结果在 int 范围内
数据范围：0 < n，m ≤ 100，保证计算结果在32位整型范围内
要求：空间复杂度 O(nm)，时间复杂度 O(nm)O(nm)
.
示例：
输入：2，1
返回值：1
.
输入：2，2
返回值：2

分析

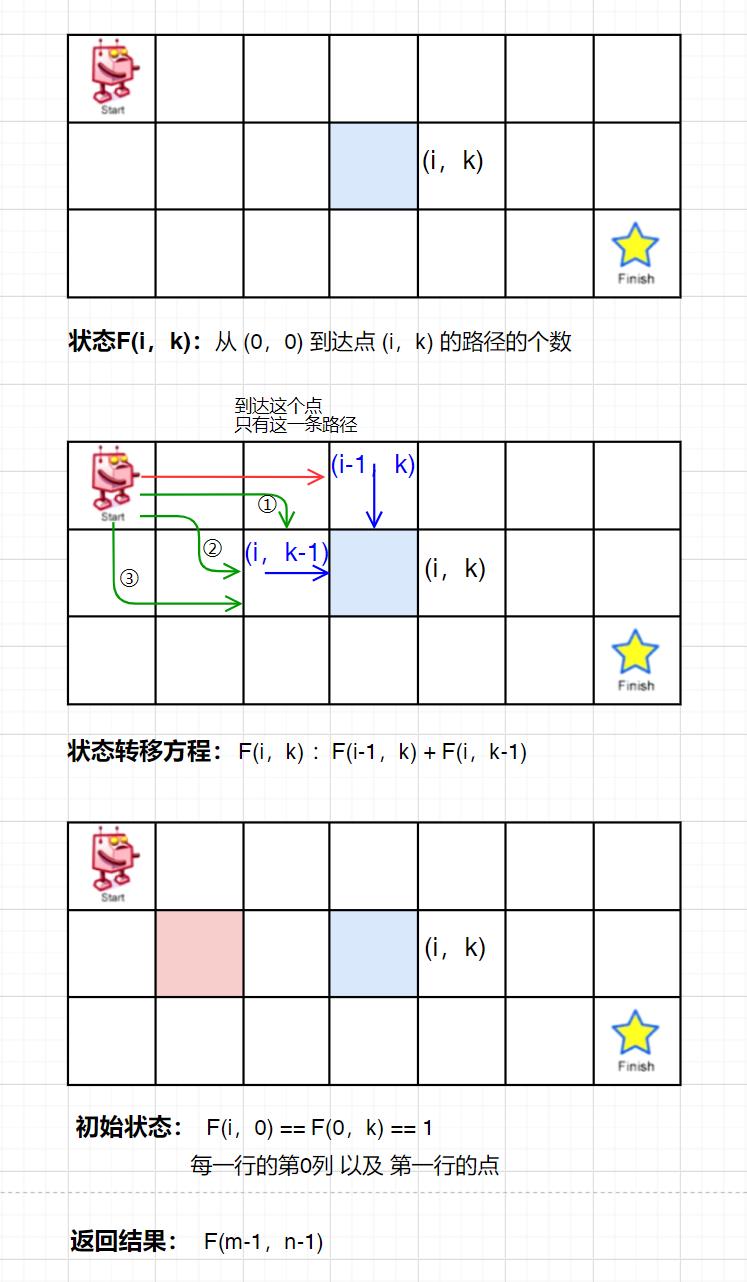
代码实现：

public int uniquePaths (int m, int n) 
    // 创建矩阵
    int[][] pathNum = new int[m][n];

    // 初始化 F(i,0) 和 F(0,k);
    for (int i = 0; i < m; i++) 
        pathNum[i][0] = 1;
    
    for (int k = 1; k < n; k++) 
        pathNum[0][k] = 1;
    
    for (int row = 1; row < m; row++) 
        for (int col = 1; col < n; col++) 
            pathNum[row][col] = pathNum[row - 1][col] + pathNum[row][col - 1];
        
    
    return pathNum[m - 1][n - 1];

2.最小路径和

题目

分析

和上一个题类似

状态 F(i，k)： 表示从 (0，0) 到达 (i，k) 的最短路径和
状态转移方程：
F(i，k) ：min( F(i-1，k)，F(i，k-1) ) + array[ i ] [ k ]

第一行：
F(0，k)：F(0，k-1) + array[0] [ k ]
第一列：
F(i，0)：F(i-1，0) + array[ i ] [0]

初始状态： F(0，0) = array[0][0]
返回结果： F(row-1，col-1)

代码实现：

public int minPathSum(int[][] grid) 
    if(grid == null || grid.length == 0 || grid[0].length == 0)
        return 0;
    
    int row = grid.length;
    int col = grid[0].length;
    // F(0,0), F(0,i), F(i,0)初始化
    for(int i = 1;i < row;i++) 
        grid[i][0] = grid[i - 1][0] + grid[i][0];
    
    for(int k = 1;k < col;k++) 
        grid[0][k] = grid[0][k - 1] + grid[0][k];
    
    for(int i = 1;i < row;i++) 
        for(int k = 1;k < col;k++) 
            grid[i][k] = Math.min(grid[i - 1][k],grid[i][k - 1]) + grid[i][k];
        
    
    return grid[row - 1][col - 1];