一些数论的模板及相关结论

Posted 2022-08-12 clover_hxy

数论总结

先从简单的发起啦。。。。。

一、整除和同余

b整除a记作b|a． a, b除以m所得的余数相同，记作a≡b (mod m) a=b(modm)两侧可以同加、减、乘、乘方 a=b(modm),gcd (a,b,m)=d，则a/d=b/d(mod m/d) a=b(modm) 有时可以写为a+xm=b+ym,x,y为整数 同余有周期性 amod b = a-(a/b)*b
这个应该比较简单吧，不解释。
二、质因数分解

最简单的方式可以通过O(sqrt(n))的方式求解。

void solve(int x)

	for (int i=2;i*i<=x;i++)
	 if (x%i==0) 
	 	num[++cnt]=i;
		while (x%i==0) x/=i; 
	 
	if (x>1) num[++cnt]=x;

但是我们其实有更快速的方法，就是提前预处理好每个数的最小质因子，然后每次不断的除掉最小质因子，得到一个新的数，不断重复上述过程，时间复杂度O(logn)

void calc()

	minp[1]=1;
	for (int i=2;i<=10000000;i++) 
		if (!pd[i]) 
			prime[++prime[0]]=i;
			minp[i]=prime[0];
		
		for (int j=1;j<=prime[0];j++)
			if (i*prime[j]>10000000) break;
			minp[i*prime[j]]=j;
			pd[i*prime[j]]=1;
			if (i%prime[j]==0) break;
		
	

void solve(int x)

	while (x!=1) 
			num[i][++num[i][0]]=minp[x];
			int t=prime[minp[x]];
			while (x%t==0) x/=t;
		

三、gcd与lcm

gcd(a,b)=gcd(a-b,b)  gcd(a,b)=gcd(a%b,a)  lcm(a,b)=a*b/gcd(a,b) 将a,b质因数分解,gcd是两因子的min,lcm是两因子的max  d|gcd(a,b)<=> d|a 且 d|b 有时简化书写将gcd(a,b)记为(a,b),lcm(a,b)为[a,b]
既然说到gcd那必然要提到欧几里得算法啦，时间复杂度应该也是O(logn)

void gcd(int x)

	int r;
	while (y)
		r=x%y;
		x=y; 
		y=r;
	
	return x;

四、phi 

先说一下phi的定义：phi(n)等于1到n中与n互质的数的个数

那么phi有什么性质呢？

当n为质数是，phi(n)=n-1,特别注意phi(1)=1

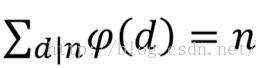懒得用markdown ，所以截图了。。。。。

phi(p^k)=(p-1)*p^(k-1) p为质数 

证明如下：令n == p^k,小于 n 的正整数共有 p^k-1 个,其中与 p 不互素的个数共 p^(k-1)-1 个，它们是 1*p,2*p,3*p ... (p^(k-1)-1)*p (p^k/p=p^(k-1),-1是因为除去本身）

phi(a)*phi(b)=phi(a*b) 这个性质应该积性函数都有吧，根据这个性质就可以用线性筛求phi啦，模板会在放在线性筛中。

与phi有关的定理——欧拉定理： 如果a,n都为正整数，且a,n互质那么a^phi(n)=1(mod n)

其实phi还可以用O(sqrt(n))的时间求出单个phi。

主要利用了一个式子：

LL _phi(LL x)
	LL ans=x;
	for(int i=2;i*i<=x;i++)
	if(x%i==0)
			ans=ans*(i-1)/i;
			while(x%i==0)x/=i;
		
	if(x>1)ans=ans*(x-1)/x;
	return ans;

五、mu 莫比乌斯函数。

莫比乌斯函数完整定义的通俗表达： 1）莫比乌斯函数μ(n)的定义域是N 2）μ(1)=1 3）当n存在平方因子时，μ(n)=0 4）当n是素数或奇数个不同素数之积时，μ(n)=-1 5）当n是偶数个不同素数之积时，μ(n)=1 注意mu也是积性函数，所以可以用线性筛求解。

反演的式子：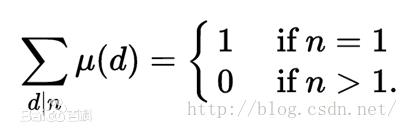 

积性函数都可以O(sqrt(n))的求解,那mu可以吗？看mu的定义，发现都有质因数有关，所以我们可以在分解质因数的同时进行记录。代码不单独贴了。

昨天新get到了一种快速求mu的方法：

当mu(x)存在次数不为1的质因子时，答案为0，我们先不考虑这张情况，只统计质因子次数都为1的数就行了。那么μ 的值实际上是-1和1互相变化的，那样就可以用一个类似状压dp的方法求出质因子是某一个状态mu的值，以及这个状态当质因子次数都为1时的因数的值。当
n<=109 时至多有 10 个质因子，所以这样做的时间复杂度是O(2^s)

这里贴zyf2000的代码。。。orz

for (int i=0;i<(1<<totp);++i)
    
        if (i)
        
            mu[i]=-mu[i^i&-i];
            d[i]=d[i^i&-i]*d[i&-i];
        
        else mu[i]=d[i]=1;
    

这个算法需要先分解质因数，totp表示的是质因数的个数，i&(-i)其实就是树状数组的lowbit，表示的是二进制下最低位1的位置，i^i&(-i)相当于消掉这一位，实现1与-1的互换，d[i]存的是这个状态的数是多少。

六、线性筛

总算到线性筛啦，线性筛顾名思义，就是时间复杂度为线性的筛法，时间复杂度O(n)

可以求解质因数,phi,mu等等。

void get_p()//欧拉筛 
	phi[1]=mu[1]=1;
	for(int i=2;i<=n;i++)
		if(!p[i])
			prime[++prime[0]]=i;
			phi[i]=i-1;mu[i]=-1;
		for(int j=1;j<=prime[0];j++)
			if(i*prime[j]>n)break;
			p[i*prime[j]]=1;
			if(i%prime[j]==0)
				mu[i*prime[j]]=0;
				phi[i*prime[j]]=phi[i]*prime[j];
				break;
			else
				phi[i*prime[j]]=phi[i]*(prime[j]-1);
				mu[i*prime[j]]=-mu[i];
			
		
	

既然说到了筛质数，那么就顺便提一下埃氏筛法，这个就是利用已知的质数筛掉他们的倍数，虽然某些情况下不如线性筛，但是当数据范围比较大（超过10^7），没法用线性筛的时候就可以用埃氏筛发来做，因为如果是合数的话至少存在一个小于sqrt(n)的质因子，所以我们可以通过枚举质因子来做。

七、逆元

费马小定理：a^(p-1)≡1 (mod p)  p是质数

逆元是求a*x=1 (mod p) ，根据上式x=a^(p-2)  这时可以用快速幂求解。

int  quickpow(int x,int num)

	int ans=1; int base=num%p;
	while (x)
		if (x&1) ans=(ans*base)%p;
		x>>=1;
		base=(base*base)%p;
	
	return ans;

那么当p不是质数的时候怎么办？

如果a,p互质，我们可以用exgcd扩展欧几里得算法来求解。

什么是扩欧？

设a,b的最大公因数为gcd ，那么，我们一定能够找到这样的 x 和 y ，使得: a*x + b*y = gcd 这是一个不定方程，有多解是一定的，但是只要我们找到一组特殊的解 x0 和 y0 那么，我们就可以用 x0 和 y0 表示出整个不定方程的通解：

        x = x0 + (b/gcd)*t

        y = y0 – (a/gcd)*t

那么乘法逆元不就可以表示成ax+y*p=1 求此时的x，不就是逆元嘛。那么由这个式子就可以知道只有gcd(a,p)=1的时候方程才有解。

void exgcd(LL a,LL b,LL &x,LL &y)  
  
    if (b==0)  
      
        x=1; y=0;  
        return;  
      
    exgcd(b,a%b,x,y);  
    LL t=y;  
    y=x-(a/b)*y;  
    x=t;  
  

那如果不满足a,p互质怎么办？我们可以将p分解，分别求解，然后用中国剩余定理合并。