数据结构与算法详解什么是哈希表，并用代码手动实现一个哈希表

Posted 2022-08-09 「零一」

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构与算法详解什么是哈希表，并用代码手动实现一个哈希表相关的知识，希望对你有一定的参考价值。

本系列文章【数据结构与算法】所有完整代码已上传 github，想要完整代码的小伙伴可以直接去那获取，可以的话欢迎点个Star哦~下面放上跳转链接

https://github.com/Lpyexplore/structureAndAlgorithm-JS

数组是我们平时常见的并且经常使用的一种数据结构，那么它具有什么优点呢？我们都知道，在我们知道数组中某元素的下标值时，我们可以通过下标值的方式获取到数组中对应的元素，这种获取元素的速度是非常快的。

但是呢，数组也是有一定的缺点的，如果我们不知道某个元素的下标值，而只是知道该元素在数组中，这时我们想要获取该元素就只能对数组进行线性查找，即从头开始遍历，这样的效率是非常低的，如果一个长度为10000的数组，我们需要的元素正好在第10000个，那么我们就要对数组遍历10000次，显然这是不合理的。

所以，为了解决上述数组的不足之处，引入了哈希表的概念，哈希表在很多语言的底层用到的非常的多，本文我们将来讲解一下哈希表。因为哈希表的底层知识很多，但是代码是非常简洁的，所以请大家耐心看完。

公众号：前端印象
不定时有送书活动，记得关注~
关注后回复对应文字领取：【面试题】、【前端必看电子书】、【数据结构与算法完整代码】、【前端技术交流群】

一、什么是哈希表

文章开头就说了，哈希表可以弥补数组的一些缺点，所以我们就可以在数组的基础上做一些改动，来实现哈希表。

我们还是先以一个具体的例子来理解一下哈希表。

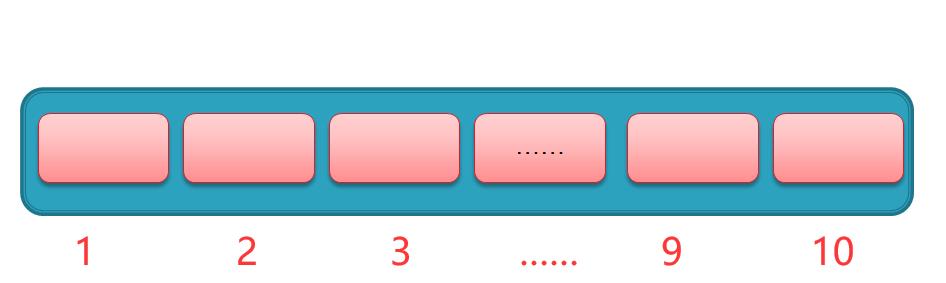
假如图书馆有十万本图书，图书管理员把它们随意地放置在书架上，到数组中就是这个样子的

此时书架上的书是无序的，突然有一个同学说我要来找 《零基础入门javascript》 这本书，那么他们只能从书架上的第一本书开始挨个往后找，直到找到这本书为止。

这就像数组中要找一个不知道下标的元素，只能遍历整个数组，这样不太好。

那么有人就要说了，那我们在将图书放置到书架上的时候，给每一本书一个下标不就好了吗？到时候找书的时候直接通过下标来找到书，这样岂不是很方便？

这话说的没错，我们平时去图书馆借书的时候，都是通过计算机来查询到一本书的编号，然后再去指定书架上找书的，那么在你查阅计算机时，计算机难道要遍历整个图书库，然后找到你要的那本书吗？这显然是不可能的，所以我们要研究出一种让计算机拿到一本书的名字时，就能得知这本书的编号的数据结构，这里就引入了哈希表的概念

为了方便我们了我们先决定一个可接受的数组长度，比如说设置数组长度为10

然后把每本书的书名看作是一个字符串，例如 "零基础入门JavaScript"，此时该字符串的长度为15，我们就分别获取每一个字符的Unicode 编码，然后用著名的秦九韶算法来将每一个Unicode 编码组合成一个很大的数。

这里先来介绍一下 秦九韶算法。秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化算法，在西方被称作霍纳算法。

这是一个一元n次多项式的求和公式，我们可以看到，在这个公式中，一共有n次加法和(n+1)*n/2次乘法

而秦九韶算法就是对该公式进行了提取公因式，最终将式子变成这样

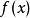
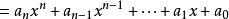
看到最终结果，我们可以看到，这个式子被简化以后，只需要进行n次乘法计算和n次加法计算了。

这样的简化过程也为计算机处理多项式的求值问题提供了很大的便利，大幅度提高了求值的效率。这也就是我们为何要使用秦九韶算法来将字符串的Unicode 编码组合成一个很大的数的原因了。

我们通过查阅 零基础入门JavaScript 中每个字符串的Unicode 编码，它们分别为 38646 、22522 、30784 、20837 、38376 、74 、97 、118 、97 、83 、99 、114 、105 、112 、116

然后我们把这些Unicode 编码代入到秦九韶算法中，得到 3.539723283210537e+26，这是一个特别特别特别大的数字，你可能想问，我们获得这么大的数干什么呢？因为我们刚才不是设定了数组的长度为10吗？所以我们将这个得到的数除以10取余，将获得的余数作为该元素在数组中的下标值。

为什么要这么做呢？因为数组的长度为10，所以数组的下标值范围为0~9，那么一个数除以10取余，那么该余数的范围是不是也是0~9呢？那不正好跟数组的下标值对应起来了吗？

讲到这里了，我再来解释一下，为什么要通过秦九韶算法获取到一个这么大的数，然后再取余得到下标值呢？这不是多此一举么，为何不直接把每一个字符的Unicode 编码相加再直接取余，这样连乘法都不用算，全是加法，计算效率更高。那么我们再来看一个例子，就知道为何要用先获取一个很大的数了：

首先，第一个字符串是 bcd，每个字符的Unicode 编码分别为 98 、99 、100，加起来等于297，297 % 10 = 7，所以字符串 bcd 在数组中的下标值就为7；
第二个字符串是 ace，每个字符的Unicode 编码分别为 97 、99 、101，加起来也等于297，所以同样的，ace 在数组中的下标值也同样为7;

此时，两个字符串的下标值就重复了，这种现象在哈希表中称为冲突，在下文我会详细讲到。话说回来，就是因为简单的相加取余会很容易就出现冲突的现象，所以我们才选择利用秦九韶算法来给每个字符串规定相应的下标值，这样能在很大程度上保证了每个元素的下标值不重复，当然了也是会有一定几率重复的，这是不可避免的。

上面将一个字符串转化为数组长度范围内的下标值的过程就称作为 哈希化，而实现哈希化的代码一般会封装在一个函数里，这个函数就叫做 哈希函数

按照上述所说的方法，对每本书的书名字符串进行哈希化，就可以使每本书获得一个下标值并存储在数组中了，之后当你要查阅一本书的编码时，你输入那本书的书名，计算机拿到以后，只需要通过哈希函数的处理，就可以获得这本书的下标值，然后瞬间获得这本书的编号。

相信大家对 哈希表 应该有了一定的了解了，如果没看懂，我们下面再慢慢讲解。

二、哈希表的优缺点

在刚才哈希表的描述中，大家一定能看出哈希表的优缺点了，这里我来给大家总结一下吧~

（1）优点

首先是哈希表的优点：

无论数据有多少，处理起来都特别的快
能够快速地进行 插入修改元素 、删除元素 、查找元素 等操作
代码简单（其实只需要把哈希函数写好，之后的代码就很简单了）

（2）缺点

然后再来讲讲哈希表的缺点：

哈希表中的数据是没有顺序的
数据不允许重复

三、冲突

前面提到了冲突，其含义就是在哈希化以后有几个元素的下标值相同，这就叫做 冲突。 那当两个元素的下标值冲突时，是后一个元素是不是要替换掉前一个元素呢？当然不是！

那么如何解决冲突这个现象呢？一般是有两种方法，即拉链法（链地址法） 和 开放地址法

（1）拉链法

这种方法是很常用的解决冲突的方法。我们还是拿上面那个例子来说，10本图书通过哈希化以后存入到长度为10的数组当中，难免有几本书的下标值是相同的，那么我们可以将这两个下标值相同的元素存入到一个单独的数组中，然后将该数组存放在他们原本所在数组的下标位置，如图

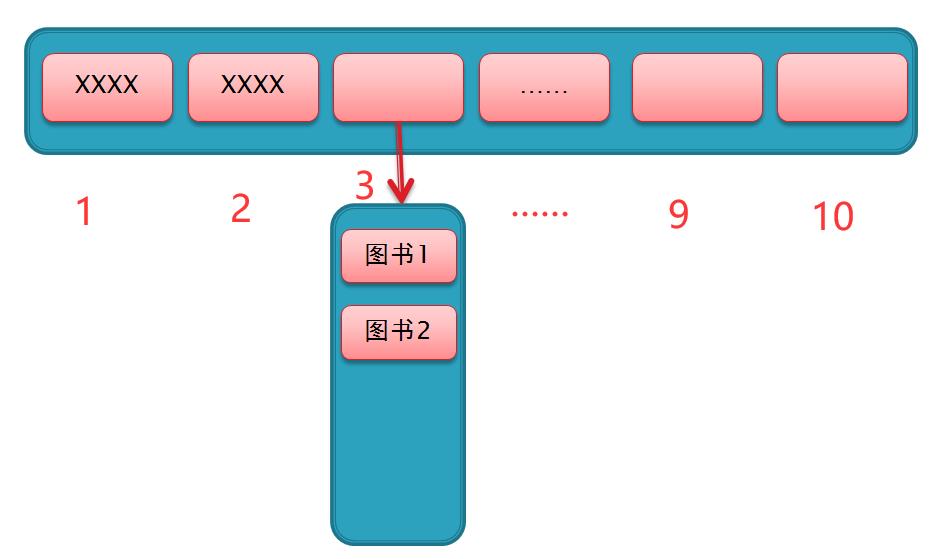
假设图书1 和 图书2 哈希化后的下标值都为3，那么我们就可以在原数组下标3的位置放一个数组，同时存放这两本图书。因此，无论是查询哪本图书，计算机获得的下标值都是3，然后再对这个位置的数组进行遍历即可获得想要的图书。

这是第一种解决冲突的方法，但使用是还是需要考虑数组长度是否合适的，之后会进行讲解。

（2）开放地址法

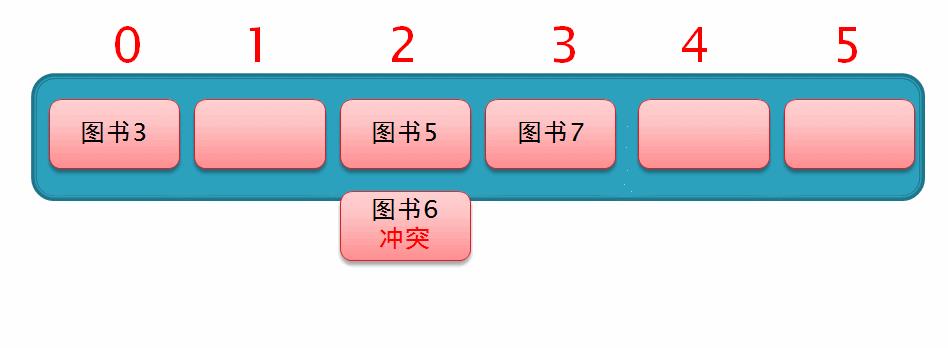
这种方法简单来说就是当元素下标值发生冲突时，寻找空白的位置插入数据。假设当前下标值为1和3的位置分别已经插入了 图书3 和 图书5，这时将 图书6 进行哈希化，发现它的下标值也是1，此时与 图书3 发生冲突，那么此时 图书6 就可以找到下一个空着的没插入元素的位置进行插入，如图

其实当发生冲突时，寻找空白的位置也有三种方法，分别是 线性探测 、二次探测 、再哈希法

1. 线性探测

顾名思义，线性探测的意思就是，当某两个元素发生冲突时，将当前索引+1，查看该位置是否为空，是的话就插入数据，否则就继续将索引+1，以此类推……直到插入数据位置。

但这种方法有一个缺点，那就是当数组中连续很长的一个片段都已经插入了数据，此时用线性探测就显得效率没那么高了，因为每次探测的步长都为1，所以这段都已经插入了数据的片段都得进行探测一次，这种现象叫做聚集。如下图，就是一个典型的聚集现象

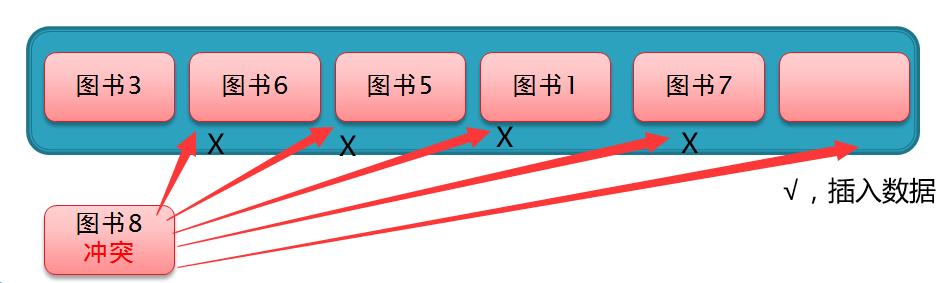
图书8 的下标值为1，与 图书3 冲突，然后进行线性探测，依次经过 图书6、5、1、7 都没有发现有空白位置可以插入，直到末尾才找到空白位置插入，这样挺不好的，所以我们可以选用 二次探测 来缓解聚集这种现象。

2. 二次探测

二次探测 在线性探测的基础上，将每次探测的步长改为了当前下标值 index + 1² 、index + 2² 、 index + 3² …… 直到找到空白位置插入元素为止

还是举一个例子来理解一下 二次探测 吧

假如现在已存入 图书3 、图书5 、图书7，如图

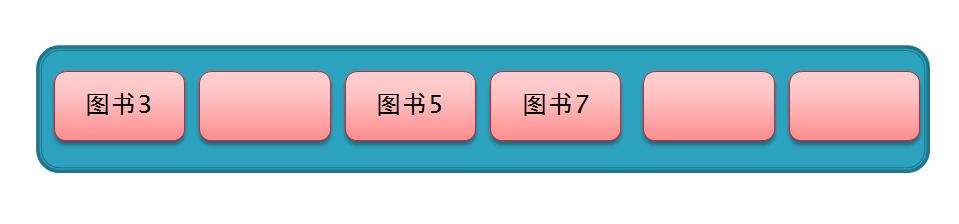
然后此时要存入一个 图书6，通过哈希化以后求得的下标值为2，与 图书5 冲突了，所以就从索引2的位置向后再移动 1² 个位置，但此时该位置上已存有数据，如下面这个动图演示

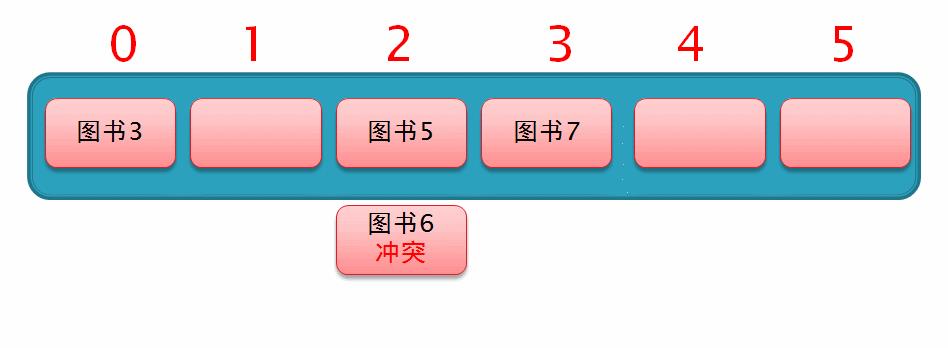
所以此时从索引为2的位置向后移动 2² 个位置，此时发现移动后的位置上也已存有数据，所以仍无法插入数据，如下面这个动图演示

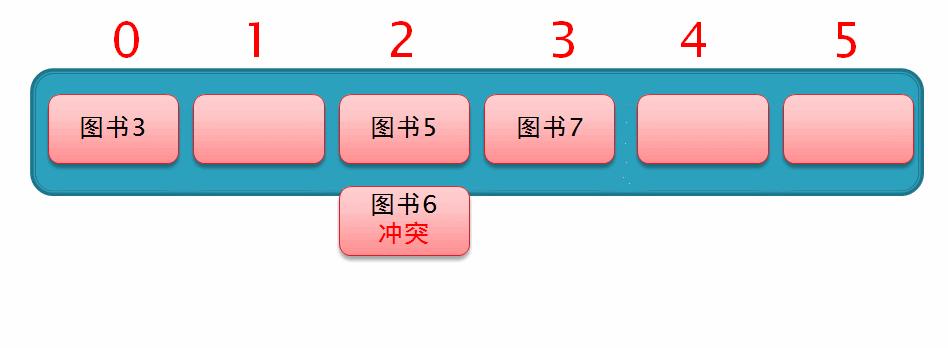
因此，我们继续从索引2的位置向后移动 3² 个位置，此时发现，移动后的位置上有空余位置，于是直接在此插入数据，这样一个二次探测的过程就完成了，如下列动图演示

我们可以看到，二次探测 在一定程度上解决了 线性探测 造成的聚集问题，但是它却在另一种程度造成了一种聚集，就比如 1² 、2² 、3² …… n² 上的聚集。所以这种方式还是有点不太好。

3. 再哈希法

再哈希法 就是再将我们传入的值进行一次 哈希化，获得一个新的探测步数 step，然后按照这个步数进行探测，找到第一个空着的位置插入数据。这在很大的程度上解决了聚集的问题。

既然要再进行哈希化获得一个探测的步数，那么这个哈希化的处理过程一定要跟第一次哈希化的处理过程不一样，这样才能确认一个合适的搜索步长，提高查找效率。

这里，我们就不用担心如何写一个不一样的哈希函数了，给大家看一个公认的比较好的哈希函数：step = constant - (key % constant)

其中，constant 是一个自己定的质数常量，且小于数组的容量； key 就是第一次哈希化得到得值。

然后我们再通过这个函数算得的步长来进行查找搜索空位置进行插入即可，这里就不做过多的演示了。

四、哈希表的扩容和减容

在了解哈希表的扩容之前，我们来了解一个概念，叫做填充因子，它表示的是哈希表中的数据个数与哈希表长度的比值。其决定了哈希表的存取数据所需的时间大小。

当我们用第一种解决冲突的办法——拉链法，填充因子最小为0，最大为无限大，这是因为该方法是通过在数组中的某个位置插入一个数组用来存储互相冲突的元素，因此，只要有可能，哈希表的长度可以很小，然后数据都存储在内置的数组中，这样填充因子就可以无限大了。

那当我们用第二种解决冲突的办法——开放地址法，填充因子最小为0，最大只能为1，这是因为开放地址法的实现原理是找哈希表中空位置插入元素，因此哈希表中的数据量不会大于哈希表的长度，从而填充因子最大也只能是1。

把哈希表比作是个教室，如果教室里坐满了人，然后让你从中找出你的朋友，那密密麻麻的，是不是特别不好找，可能会眼花缭乱；但是如果这个教室里只坐了 2/3 或者 1/2 的人，那么人群看起来就没那么密密麻麻，那让你找到你的朋友也许会相对容易一点。

也正因为这样的情况，我们可以在适当的时候根据填充因子的大小对哈希表的长度进行扩大，从而减小填充因子的大小，降低我们数据存取所耗费的时间。

这里我们就将填充因子等于 0.75 作为哈希表扩容的临界点，同时会在后面封装哈希表的时候实现扩容。

当然，填充因子太小也是不合适地，所以我们也会在适当的地方添加减容功能，即将填充因子等于 0.25 作为哈希表减容的临界点。

五、哈希表的方法

老规矩，我们在封装哈希表之前，先来看看哈希表常见的方法都有哪些

方法	含义
put()	向哈希表中插入数据或修改哈希表中数据
get()	获取哈希表中的某个数据
del()	删除哈希表中某个数据
isEmpty()	判断哈希表是否为空
size()	返回哈希表内元素个数
resize()	改变哈希表容量，并将数据放到正确的位置上
isPrime()	判断某个数是不是质数
toPrime()	获取离某个数最近的质数

六、用代码实现哈希表

前提：

本文选用链地址法解决冲突问题
涉及到常量的地方，都选用质数，例如哈希表容量、霍纳算法的常量等。因为在数论上，使用质数可以尽可能地使数据在哈希表中均匀分布

（1）创建一个构造函数

首先创建一个大的构造函数，用于存放哈希表的一些属性和方法。

function HashTable() 
	// 属性
	
	// 用于存储数据
    this.storage = []
    
    // 统计哈希表内数据个数
    this.count = 0
    
    // 设定哈希表初始长度
    this.length = 7

因为我们是通过数组来实现的哈希表，所以设置了属性 storage 来存储数据；然后定义了属性 count 用于统计哈希表内的数据个数，方便之后用于计算填充因子；最后定义了属性 length 设定了哈希表的初始长度为质数7

（2）封装哈希函数

在文章的开头，我就用霍纳算法讲解了哈希化的过程，因此我们在封装哈希函数时，就也通过霍纳算法的最终化简结构来实现

这里，我放上霍纳算法的化简结果，方便大家观看学习

P(n) = $a_0$ + x( $a_1$ +x( $a_2$ +…+ x( $a_n$ − 1 + x $a_n$ ) ) )

我们来看一下代码

function HashTable() 
	// 属性
	
	// 用于存储数据
    this.storage = []
    
    // 统计哈希表内数据个数
    this.count = 0
    
    // 设定哈希表初始长度
    this.length = 7

	//封装哈希函数
    HashTable.prototype.hashFunc = function (str, size) 
        let hashCode = 0

        //取一个很大的数
        for (let i = 0; i < str.length; i ++) 
            hashCode = 37 * hashCode + str.charCodeAt(i)
        
        
        //取余
        return hashCode % size

这里的霍纳算法中的常数我就随便取了一个质数37，大家也可以随便选别的稍微大一点的质数

哈希函数接收两个参数，第一个参数为 str ，即我们之后传入数据的 key ；第二个参数为 size ，即哈希表的长度，所以可以直接进行调用我们设定的属性 this.length

（3）实现put()方法（不具备扩容功能）

put()方法就是向哈希表插入数据或者修改哈希表中某数据。

该方法接收两个参数，第一个参数为 key；第二个参数为 value 。即相当于传入一个键值对

实现思路：

通过哈希函数，将 key 哈希化，获取一个索引 index
判断哈希表 storage 数组的索引 index 上有无数据，若无，则直接在该位置上创建一个空数组 arr，并把我们传入的键值对打包放到一个新的数组中存到 arr 中
若有数据，则遍历该索引上的数组每个元素，比对每个元素的 key 是否与我们传入的 key 相等，若有查询到相等的值，则用我们传入的 value 替换查询到的该元素中的 value ，这就实现了修改数据的功能
若没有查询到相等的值，则直接将我们的键值对打包放到一个新的数组中存储到哈希表 index 索引上的数组中去，此时 this.count + 1

为了方便大家理解，我用动图来给大家演示该方法的实现过程

首先是插入数据操作

接下来是修改数据操作

我们来看一下代码

function HashTable() 
	// 属性
	
	// 用于存储数据
    this.storage = []
    
    // 统计哈希表内数据个数
    this.count = 0
    
    // 设定哈希表初始长度
    this.length = 7

	//封装哈希函数
    HashTable.prototype.hashFunc = function (str, size) 
        let hashCode = 0

        //取一个很大的数
        for (let i = 0; i < str.length; i ++) 
            hashCode = 37 * hashCode + str.charCodeAt(i)
        
        
        //取余
        return hashCode % size
    

	// 插入或修改数据
    HashTable.prototype.put = function (key, value) 
        // 1.哈希化获得下标值
        let index = this.hashFunc(key, this.length)
        let current = this.storage[index]

        // 2.判断该下标值的位置是否有数据
        // 2.1无数据
        if(!current) 
            this.storage[index] = [[key, value]]
            this.count ++
            return;
        
        
		// 2.2有数据
		// 3.遍历对应索引上的数组
        for (let i = 0; i < current.length; i ++) 
            // 3.1已存在相同数据
            if(current[i][0] === key) 
                current[i][1] = value
                return;
            
        
        
        // 3.2未存在相同数据,直接添加数据
        current.push([key, value])
        this.count ++

我们来使用一下该方法

let ht = new HashTable()

// 执行put()方法6次
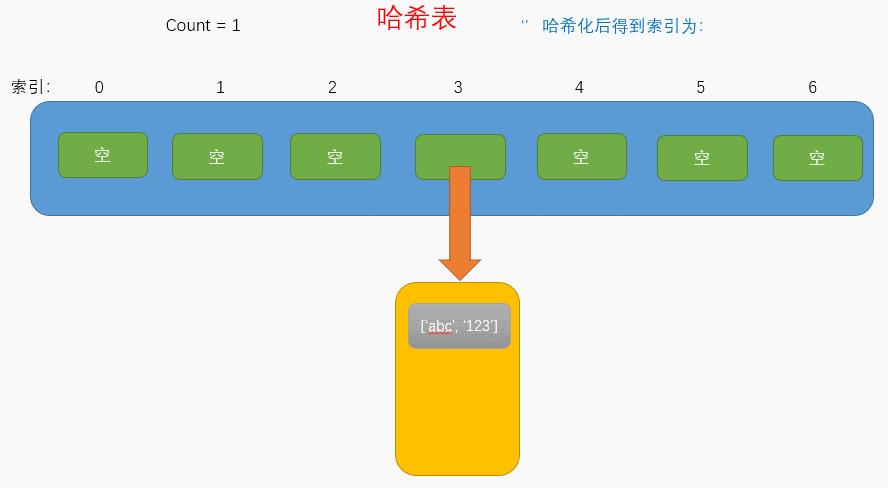
ht.put('abc', '123')
ht.put('hgf', '124')
ht.put('wds', '125')
ht.put('wer', '126')
ht.put('kgl', '127')
ht.put('kmg', '128')

// 查看哈希表内数据个数
console.log(ht.count)              // 6

// 通过storage属性查看一下哈希表的内部结构
console.log(ht.storage)

/* storage打印结果
[
  [ [ 'wds', '125' ], [ 'kgl', '127' ], [ 'kmg', '128' ] ],
  [ [ 'wer', '126' ] ],
  <1 empty item>,
  [ [ 'hgf', '124' ] ],
  [ [ 'abc', '123' ] ]
]
*/

此时的哈希表内部是这样的

（4）实现get()方法

get()方法是用于查询哈希表中某个数据。该方法直接收一个参数，即用于查询的 key

实现思路：

通过哈希函数，将 key 哈希化，获取一个索引 index
判断哈希表 storage 数组的索引 index 上有无数据，若无，则返回 false
若有数据，则遍历该索引上的数组每个元素，比对每个元素的 key 是否与我们传入的 key 相等，若有查询到相等的值，则返回该值的 value
若无数据，则返回 false

思路和代码都比较简单，我们直接来看代码

function HashTable() 
	// 属性
	
	// 用于存储数据
    this.storage = []
    
    // 统计哈希表内数据个数
    this.count = 0
    
    // 设定哈希表初始长度
    this.length = 7

	//封装哈希函数
    HashTable.prototype.hashFunc = function (str, size) 
        let hashCode = 0

        //取一个很大的数
        for (let i = 0; i < str.length; i ++) 
            hashCode = 37 * hashCode + str.charCodeAt(i)
        
        
        //取余
        return hashCode % size
    

	// 获取数据
    HashTable.prototype.get = function (key) 
        // 1.获取相应的下标值
        let index = this.hashFunc(key, this.length)
        let current = this.storage[index]
		
		// 2.判断该下标值的位置是否有数据
        // 2.1 若该下标值位置不存在任何数据，则查找失败
        if(!current) 
            return false
        

        // 2.2 该下标值位置有数据
        // 3. 进行遍历查找
        for(let i in current) 
            // 3.1 找到对应数据并返回value
            if(current[i][0] === key) 
                return current[i][1]
            
        

        // 3.2 没有找到对应数据，返回false
        return false

我们来使用以下该方法

let ht = new HashTable()

// 执行put()方法 6次
ht.put('abc', '123')
ht.put('hgf', '124')
ht.put('wds', '125')
ht.put('wer', '126')
ht.put('kgl', '127')
ht.put('kmg', '128')

// 执行get()方法，获取 key为 'hgf' 的值
console.log(ht.get('hgf'))           // 124

（5）实现del()方法（不具备减少容量功能）

del()方法是删除哈希表中某个数据。该方法接收一个参数 key

实现思路：

通过哈希函数，将 key 哈希化，获取一个索引 index
判断哈希表 storage 数组的索引 index 上有无数据，若无，则返回 false ，表示删除失败
若有数据，则遍历该索引上的数组每个元素，比对每个元素的 key 是否与我们传入的 key 相等，若有查询到相等的值，则直接删除该值，此时 this.count --，并返回被删除元素的 value值
若没有查询到相等的值，则返回 false ，表示删除失败

我们来看一下代码

function HashTable() 
	// 属性
	
	// 用于存储数据
    this.storage = []
    
    // 统计哈希表内数据个数
    this.count = 0
    
    // 设定哈希表初始长度
    this.length = 7

	//封装哈希函数
    HashTable.prototype.hashFunc = function (str, size) 
        let hashCode = 0

        //取一个很大的数
        for (let i = 0; i < str.length; i ++) 
            hashCode = 37 * hashCode + str.charCodeAt(i)
        
        
        //取余
        return hashCode % size
    

	// 删除数据
    HashTable.prototype.del = function (key) 
        // 1.获取相应的下标值
        let index = this.hashFunc(key, this.length)
        let current = this.storage[index]
		
		// 2. 判断该索引位置有无数据
        // 2.1 该下标值位置没有数据，返回false，删除失败
        if(!current) 
            return false
        

        // 2.2 该下标值位置有数据
        // 3. 遍历数组查找对应数据
        for (let i in current) 
        	let inner = current[i]
            // 3.1 找到对应数据了，删除该数据
            if(inner[0] === key) 
                current.splice(i, 1)
                this.count --
                return inner[1]
            
        

        // 3.2 没有找到对应数据，则删除失败，返回false
        return false

我们来使用一下该方法

let ht = new HashTable()

// 执行put()方法 6次
ht.put('abc', '123')
ht.put('hgf', '124')
ht数据结构与算法哈希算法的原理和应用详解！
 理解哈希表
 字符串哈希算法（以ELFHash详解）
 哈希表与哈希（Hash）算法
 数据结构与算法实例(哈希表实现)
 数据结构与算法重新发明哈希表 Hashtable