卡尔曼滤波器（目标跟踪一）（上）

Posted 2022-08-09 Huterox

文章目录

• 单目标检测
• • IOU跟踪
  • • 目标丢失
    • 人群密集
• 卡尔曼滤波直观理解
• • 状态方程
  • 噪声
  • 协方差
• 卡尔曼公式
• • 案例运用

本文主要是针对目标跟踪算法进行一个学习编码，从比较简单的卡尔曼滤波器开始，到后面的deepsort 和最后与yolo算法进行整合，到最后手动实现目标跟踪框架的流程进行。本着，无法造轮子就没有彻底理解的原则进行学习。那么废话不多说开始了。（收藏>点赞？VIP:Free，白嫖可耻，拒接白嫖）

单目标检测

ok，我们先从单目标检测开始说起。假设我们用Yolo算法检测到了一个目标，假设我们的数据源是视频，我们要跟踪的是其中一个人，也就是下面这种图片：假设要跟踪红框当中的男子，现在的图片是摄像头某一个时刻某一帧的情况。

接下来当男子移动的时候，我还想再跟踪这个家伙，并且我还要把他的运动轨迹搞出来。

假设这个目标框我们是使用yolo算法识别出来的，我们知道如果是这个yolo算法识别出来的话，那么我们得到的就是这个目标的bbox和对应的类别。

当摄像头下一帧或者下一秒出现的时候，我们的算法得到的就只是它新的一个bbox也就是在图片当中他的坐标。
那么问题来了周围那么多人，我肯定也是会识别出来的，也就是说，下一秒下一个时刻yolo算法识别得到的结果是一群人的坐标，我如何在中多bbox里面找到红色框的人的这个时刻的位置。

IOU跟踪

使用IOU显然是一个最容易想到的问题，也就是说，假设我们知道要跟踪的人一开始的bbox，那么在一个时刻，我可以去遍历所有的bbox,然后找到和上一个时刻bbox的IOU最大的一个框出来，那么是不是可以说是当前这个IOU最大的框就是这个男人的位置呢？

理想状况下显然是这样的：

尽管这个时刻识别出了好几框，但是我们依然可以找到这个目标现在这个时刻的位置。

然而显然这里面有很多问题。

目标丢失

首先最容易想到的问题是，目标丢失，也就是，如果在某一个时刻，遇到障碍物，那个目标的位置丢失了，那么下一个时刻我们再计算IOU的话显然计算的就是和别的目标的框，这样一来识别到的或者跟踪的目标就发生了偏移。假设就算是当前只有一个目标，没有其他的，一旦发生遮挡并且目标移动速度很快，下一个时刻目标框和上一个目标框的IOU计算值为0一样不行。

人群密集

这个问题在这张图当中很好演示，在2D平面是我们很容易发现，那个黄色衣服的女人和我们的目标的框的IOU是重合很大的，如果那个女人稍微走的慢一点，会发生什么？就很有可能那个女人在这个时刻的框和目标上个时刻的框重合，然后目标转移了。

所以为了解决这个问题，我们显然需要记录更多的信息。

我们现在先忽略人群密集的情况，并且只考虑单目标跟踪，并且我们还假设这个人是线性移动的。

卡尔曼滤波直观理解

所以为了解决我们假设的东西，我们这里需要有引入这个玩意，这个东西主要是用于线性的一个状态处理。

用在我们这里的话其实是类似与根据当前的状态去预测一下目标后面可能存在的位置，这样的话下一次我们检测到的bbox可以和我们预测的进行iou计算，从而确定我们目标的一个运动状态。

所以这里涉及到两个东西，上一个时刻的状态，和这个时刻的观察状态。

因此咱们这里对卡尔曼来说刚好对应两个玩意。

状态方程，观察方程。

状态方程

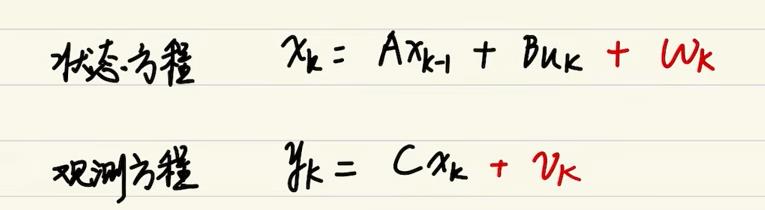
其中wk 为过程噪声，A,B,C为系数 Uk 表示的是状态的一个变化量，vk是观察噪声。

什么意思咧，我们假设人理想状态下做匀速直线运动，那么 xk = xk-1 + dt*v 但是实际上,人不可能真的做匀速运动，他一定有波动的，所以加上wk

那么yk什么意思呢，xk 是我们算出来的，实际上我们还可以通过设备观察，那么观察和我们计算的xk存在一个C的系数关系，然后加上观察的一个噪声，也就是误差，最后我们的观察方程与状态方程呈现如上关系。

他们之间的关系如下：

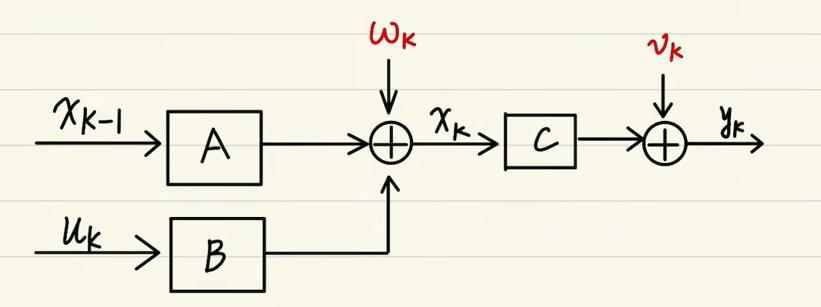
显然的话，我们的那个xk应该是作为估计值的。

噪声

之后是咱们的噪声，这个噪声说白了在这里就是误差的意思。默认假设是服从正太分布的一个误差。

现在我们大概知道了他的一个运作的，我们实际的一个X肯定是在我们预测的X和我们观察到的X之间的一个交集产生的。

由于我们的过程和观察都是由加入噪声的，所以我们的的X，Y过程和预测也是各自满足一个高斯分布的。
也就是下面这样的：

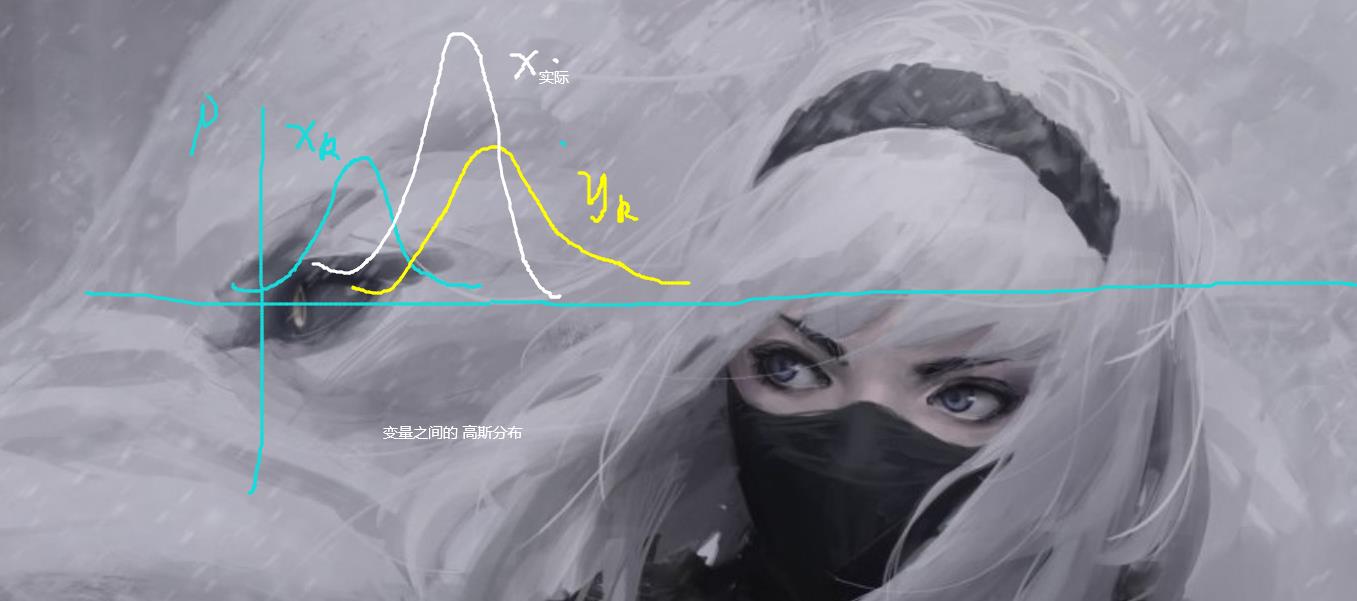
协方差

前面我们对正规的过程有了了解，那么现在还有个问题就是这个对应的A，B，C的参数如何确定。

那么这一点就需要使用到咱们的这个协方差了，无相关协方差为0 正相关（绝对）为1，负相关（绝对）为-1 这样一来就可以确定我们这个系数的一个样子。



上面是来自于知乎大佬的一个解释：
链接：https://zhuanlan.zhihu.com/p/266161140

我们这里就简单提一下高纬度的，二维的一个情况，因为一维的话其实就是我们的方差，二维的话，一般情况下，也不会去没事当作线代去算（手算），所以要提一下。

他的表示是这样的

同理如果是多维度的，比如三维是这样的：

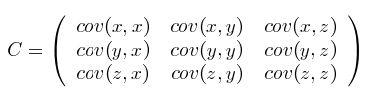
卡尔曼公式

说了这么多，对这个玩意进行初步总结就是：
使用上一次的结果，去推测当前的值，然后使用当前的观测值去修正，最后得到结果。

用公式表述就是这样的：

那个P就是咱们的协方差，我们前期提到的ABC系数。

这个P显然是需要更新的，然后那个K和咱们的P是存在一个关系的，而这个K显然就是卡尔曼系数，Z是观测的值。 所以总体是就是这关系，我们如果用于目标跟踪的话，显然我们要的是观察和X预测的一个IOU。

不过这里显然是矩阵的形式（干完这一票，说啥得把线代好好再过过）
而且你也发现了，咱们这个还是基于统计学的一个玩意。感兴趣的我可以在来一篇推导VC维度的玩意（因为手稿整理很麻烦，所以no blog)

案例运用

ok,现在我们比啊目标追踪来看看咱们的一个用法，推导。

我们依然是假设目标是线性运动的，所以影响X位置的变量有：

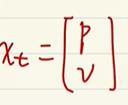
模型可以表示为：

提取出来：

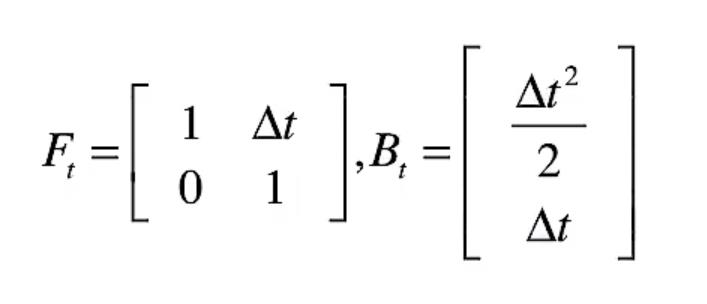
得到第一个方程：

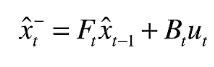
同理，第二个公式的话就是咱们的协方差的一个公式：

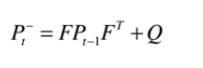
这部分的话，因为手稿和公式编辑的问题，先挪到下一部分