HDU 5883 The Best Path(并查集+欧拉回路 or 欧拉路)——2016 ACM/ICPC Asia Regional Qingdao Online

Posted 2022-07-31 queuelovestack

此文章可以使用目录功能哟↑(点击上方[+])

 HDU 5883 The Best Path

Accept: 0    Submit: 0
Time Limit: 9000/3000 MS (Java/Others)    Memory Limit: 65535/32768 K (Java/Others)

 Problem Description

Alice is planning her travel route in a beautiful valley. In this valley, there are N lakes, and M rivers linking these lakes. Alice wants to start her trip from one lake, and enjoys the landscape by boat. That means she need to set up a path which go through every river exactly once. In addition, Alice has a specific number (a1,a2,...,an) for each lake. If the path she finds is P0→P1→...→Pt, the lucky number of this trip would be aP0 XOR aP1 XOR ... XOR aPt. She want to make this number as large as possible. Can you help her?

 Input

The first line of input contains an integer t, the number of test cases. t test cases follow.

For each test case, in the first line there are two positive integers N (N≤100000) and M (M≤500000), as described above. The i-th line of the next N lines contains an integer ai(∀i,0≤ai≤10000) representing the number of the i-th lake.

The i-th line of the next M lines contains two integers ui and vi representing the i-th river between the ui-th lake and vi-th lake. It is possible that ui=vi.

 Output

For each test cases, output the largest lucky number. If it dose not have any path, output "Impossible".

 Sample Input

2
3 2
3
4
5
1 2
2 3
4 3
1
2
3
4
1 2
2 3
2 4

 Sample Output

2
Impossible

 Problem Idea

解题思路:

【题意】
n个点,每个点有一个值ai,m条边

Alice从某个点出发,恰好经过每条边一次

问Alice走过的路线中,所经过的点的异或值最大为多少

【类型】
并查集+欧拉回路 or 欧拉路
【分析】
首先,题目要求每条边恰好经过一次

那我们暂且先不管如何能使点的异或值最大

单纯考虑怎样才能经过每条边恰好一次

这考查的无疑是欧拉回路 or 欧拉路

那如何判断图中是否存在欧拉回路 or 欧拉路呢?

这个是有一个定理的

无向图存在欧拉回路的充要条件:无向图G具有一条欧拉回路,当且仅当G是连通的,并且所有结点度数全为偶数。

无向图存在欧拉路的充要条件:无向图G具有一条欧拉路,当且仅当G是连通的,且有零个或两个奇数度结点。

可见欧拉回路和欧拉路都和结点的度数有关,且图还需是连通的

但是貌似这道题数据比较水,网上很多人的题解都没有判是否连通,比如下列这种情况,不判连通显然是过不了的

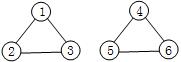
如图所示,不管选取哪个点,都无法恰好经过每条边一次

那判连通的话,并查集就能实现了

考虑完"Impossible"的情况之后,我们需要来求解如何才能使经过的点异或值最大

分两种情况:

①图中存在两个奇数度结点

这种情况下,图中存在欧拉路,路线的起点和终点分别是那两个奇数度结点,如下图

起点是结点8,终点是结点6

当然,起点是结点6,终点是结点8也是可以的

不过,不管是哪种走法,我们都可以发现

对于偶数度结点,假设度数为k,那么走的路线中必定会经过该点k/2次

比如说某点度数为4,那么必定要到达该点2次,从这点出去2次,这样才能保证与该点相连的四条边都走到

再考虑到异或运算中,一个数x,它异或本身的值等于0,即x^x=0

那我们只要考虑k/2是奇数还是偶数就可以了,偶数的话,意味着该点对异或值的贡献为0,否则贡献为a[i]

另外,最重要的一点是,欧拉路的起点和终点(即奇数度结点)会多贡献一次,要记得计算在内

②图中所有结点度数全为偶数

这种情况下,图中具有欧拉回路,这意味着路线必定是从某点出发再回到该点

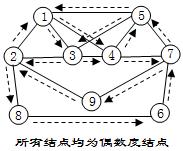
这种情况其实与欧拉路相类似,只是由于起点会多贡献一次,所以要使得异或值最大,我们可以遍历每个点

假设以点i作为起点,然后取最大值即可

【时间复杂度&&优化】
O(nlogn)

题目链接→HDU 5883 The Best Path

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 100005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
int a[N],degree[N],s[N],vis[N];
int fun(int x)

    if(s[x]!=x)
        s[x]=fun(s[x]);
    return s[x];

int main()

    int t,n,m,i,u,v,k,c,ans,tmp;
    scanf("%d",&t);
    while(t--)
    
        ans=c=k=0;
        memset(vis,0,sizeof(vis));
        memset(degree,0,sizeof(degree));
        scanf("%d%d",&n,&m);
        for(i=1;i<=n;i++)
        
            scanf("%d",&a[i]);
            s[i]=i;
        
        for(i=0;i<m;i++)
        
            scanf("%d%d",&u,&v);
            degree[u]++;
            degree[v]++;
            s[fun(u)]=fun(v);
        
        for(i=1;i<=n;i++)
            vis[fun(i)]++;
        for(i=1;i<=n;i++)
        
            if(vis[i]>1)
                k++;
            if(degree[i]%2)
                c++;
        
        if(k>1||c!=0&&c!=2)
        
            puts("Impossible");
            continue;
        
        for(i=1;i<=n;i++)
            if(degree[i]%2)
            
                if((degree[i]/2+1)%2)
                    ans^=a[i];
            
            else
            
                if(degree[i]/2%2)
                    ans^=a[i];
            
        if(!c)
            for(tmp=ans,i=1;i<=n;i++)
                if(vis[fun(i)]>1)
                    ans=max(ans,tmp^a[i]);
        printf("%d\\n",ans);
    
    return 0;

菜鸟成长记