HDU 5882 Balanced Game(其实间接考查了欧拉回路)——2016 ACM/ICPC Asia Regional Qingdao Online

Posted 2022-07-31 queuelovestack

此文章可以使用目录功能哟↑(点击上方[+])

 HDU 5882 Balanced Game

Accept: 0    Submit: 0
Time Limit: 3000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

 Problem Description

Rock-paper-scissors is a zero-sum hand game usually played between two people, in which each player simultaneously forms one of three shapes with an outstretched hand. These shapes are "rock", "paper", and "scissors". The game has only three possible outcomes other than a tie: a player who decides to play rock will beat another player who has chosen scissors ("rock crushes scissors") but will lose to one who has played paper ("paper covers rock"); a play of paper will lose to a play of scissors ("scissors cut paper"). If both players choose the same shape, the game is tied and is usually immediately replayed to break the tie.

Recently, there is a upgraded edition of this game: rock-paper-scissors-Spock-lizard, in which there are totally five shapes. The rule is simple: scissors cuts paper; paper covers rock; rock crushes lizard; lizard poisons Spock; Spock smashes scissors; scissors decapitates lizard; lizard eats paper; paper disproves Spock; Spock vaporizes rock; and as it always has, rock crushes scissors.

Both rock-paper-scissors and rock-paper-scissors-Spock-lizard are balanced games. Because there does not exist a strategy which is better than another. In other words, if one chooses shapes randomly, the possibility he or she wins is exactly 50% no matter how the other one plays (if there is a tie, repeat this game until someone wins). Given an integer N, representing the count of shapes in a game. You need to find out if there exist a rule to make this game balanced.

 Input

The first line of input contains an integer t, the number of test cases. t test cases follow.

For each test case, there is only one line with an integer N (2≤N≤1000), as described above.

Here is the sample explanation.

In the first case, donate two shapes as A and B. There are only two kind of rules: A defeats B, or B defeats A. Obviously, in both situation, one shapes is better than another. Consequently, this game is not balanced.

In the second case, donate two shapes as A, B and C. If A defeats B, B defeats C, and C defeats A, this game is balanced. This is also the same as rock-paper-scissors.

In the third case, it is easy to set a rule according to that of rock-paper-scissors-Spock-lizard.

 Output

For each test cases, output "Balanced" if there exist a rule to make the game balanced, otherwise output "Bad".

 Sample Input

3
2
3
5

 Sample Output

Bad
Balanced
Balanced

 Problem Idea

解题思路:

【题意】
类似于"剪刀石头布"的游戏,只是"剪刀石头布"只有三种形态(剪刀、石头、布),而本题有n种形态

问,在游戏有n种形态的条件下,是否存在一种规则,能够保证不管你出什么,胜利都是50%

【类型】
欧拉回路
【分析】
暂且先不管如何判断n种形态的游戏是不是"Balanced"的

我们知道的是n=3和n=5时,游戏都是"Balanced"的

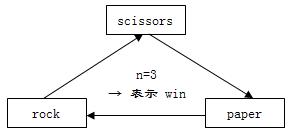
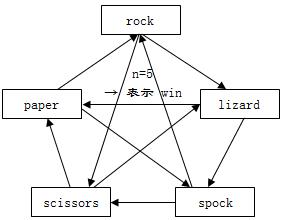
而n=2时,游戏是"Bad"的

or

而由上述几幅图,我们可以发现,当且仅当每个结点的入度等于出度时,该游戏才是"Balanced"的

而有向图存在欧拉回路的充要条件:
一个有向图存在欧拉回路,当且仅当所有顶点的入度等于出度且该图是连通图

这就对应上了

再考虑无向图存在欧拉回路的充要条件:
一个无向图存在欧拉回路,当且仅当该图所有顶点度数都为偶数,且该图是连通图

由于无向图转化为有向图,只是给每条边选定一个方向而已

所以此题就转变成了判断n为多少时存在欧拉回路

答案是每个结点的度数均为偶数

显然只有n为奇数时,一个结点能与另外的n-1(偶数)个结点相连,度数为n-1(偶数)

故n为奇数,输出"Balanced";否则,输出"Bad"

【时间复杂度&&优化】
O(1)

题目链接→HDU 5882 Balanced Game

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 100005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
int a[N],degree[N],s[N],vis[N];
int fun(int x)

    if(s[x]!=x)
        s[x]=fun(s[x]);
    return s[x];

int main()

    int t,n;
    scanf("%d",&t);
    while(t--)
    
        scanf("%d",&n);
        if(n&1)
            puts("Balanced");
        else
            puts("Bad");
    
    return 0;

菜鸟成长记