万字总结图解堆算法链表栈与队列（多图预警）

Posted 2022-07-31 nomasp

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了万字总结图解堆算法链表栈与队列（多图预警）相关的知识，希望对你有一定的参考价值。

堆算法

什么是堆

堆（heap），是一类特殊的数据结构的统称。它通常被看作一棵树的数组对象。在队列中，调度程序反复提取队列中的第一个作业并运行，因为实际情况中某些时间较短的任务却可能需要等待很长时间才能开始执行，或者某些不短小、但很重要的作业，同样应当拥有优先权。而堆就是为了解决此类问题而设计的数据结构。

二叉堆是一种特殊的堆，二叉堆是完全二叉树或者近似完全二叉树，二叉堆满足堆特性：父节点的键值总是保持固定的序关系于任何一个子节点的键值，且每个节点的左子树和右子树都是一个二叉堆。

当父节点的键值总是大于任何一个子节点的键值时为最大堆，当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。

为了更加形象，我们常用带数字的圆圈和线条来表示二叉堆等，但其实都是用数组来表示的。如果根节点在数组中的位置是1，第n个位置的子节点则分别在2n和2n+1位置上。

如下图所描的，第2个位置的子节点在4和5，第4个位置的子节点在8和9。所以我们获得父节点和子节点的方式如下：

PARENT(i)
1   return 小于或等于i/2的最大整数

LEFT-CHILD(i)
1   return 2i

RIGHT-CHILD(i)
1   return 2i+1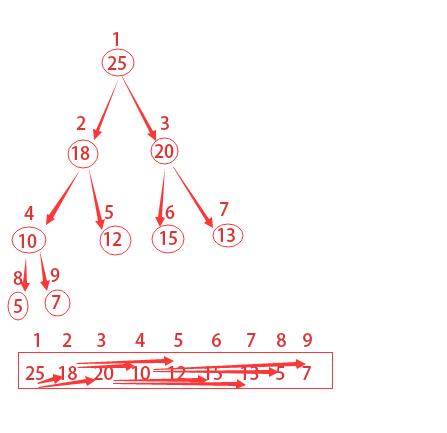

假定表示堆的数组为 $A$ ，那么 $A.length$ 通常给出数组元素的个数， $A.heap-size$ 表示有多少个堆元素存储在该数组中。这句话略带拗口，也就是说数组 $A[1...A.length]$ 可能都有数据存放，但只有 $A[1...A.heap-size]$ 中存放的数据才是堆中的有效数据。毫无疑问 $0\\leq A.heap-size\\leq A.length$ 。

最大堆除了根以外所有结点i都满足： $A[PARENT(i)]\\geq A[i]$ 。

最小堆除了根以外所有结点i都满足： $A[PARENT(i)]\\leq A[i]$ 。

一个堆中结点的高度是该结点到叶借点最长简单路径上边的数目，如上图所示编号为4的结点的高度为1，编号为2的结点的高度为2，树的高度就是3。

包含n个元素的队可以看作一颗完全二叉树，那么该堆的高度是 $\\Theta(lgn)$ 。

通过MAX-HEAPIFY维护最大堆

程序中，不可能所有的堆都天生就是最大堆，为了更好的使用堆这一数据结构，我们可能要人为地构造最大堆。

如何将一个杂乱排序的堆重新构造成最大堆，它的主要思路是：

从上往下，将父节点与子节点以此比较。如果父节点最大则进行下一步循环，如果子节点更大，则将子节点与父节点位置互换，并进行下一步循环。注意父节点要与两个子节点都进行比较。

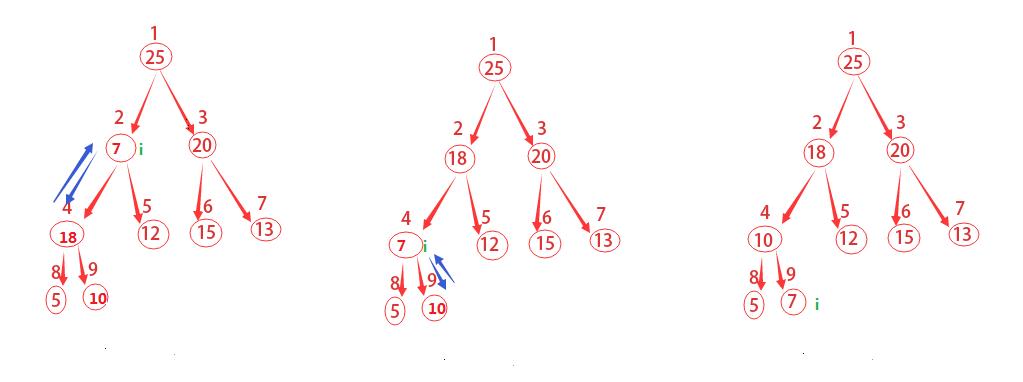
如上图说描述的，这里从结点为2开始做运算。先去 $l$ 为4， $r$ 为5，将其与父节点做比较，发现左子节点比父节点更大。因此将它们做交换，设4为最大的结点，并继续以结点4开始做下一步运算。

因此可以给出伪代码如下：

MAX-HEAPIFY(A,i)
1   l=LEFT-CHILD(i)
2   r=RIGHT-CHILD(i)
3   if l<=A.heap-size and A[l]>A[i]
4       largest=l
5   else 
6       largest=i
7   if r<=A.heap-size and A[r]>A[largest]
8       largest=r
9   if largest != i
10      exchange A[i] with A[largest]
11      MAX-HEAPIFY(A,largest)

在以上这些步骤中，调整A[i]、A[l]、A[r]的关系的时间代价为 $\\Theta(1)$ ，再加上一棵以i的子节点为根结点的子树上运行MAX-HEAPIFY的时间代价（注意此处的递归不一定会发生，此处只是假设其发生）。因为每个子节点的子树的大小至多为 $2n/3$ （最坏情况发生在树的底层恰好半满的时候）。因此MAX-HEAPIFY过程的运行时间为：

$T(n)\\leq T(2n/3)+\\Theta(1)$

也就是：

$T(n)=O(lgn)$

通过BUILD-MAX-HEAP构建最大堆

前面我们通过自顶向下的方式维护了一个最大堆，这里将通过自底向上的方式通过MAX-HEAPIFY将一个 $n=A.length$ 的数组 $A[1...n]$ 转换成最大堆。

回顾一下上面的图示，其总共有9个结点，取小于或等于9/2的最大整数为4，从4+1，4+2，一直到n都是该树的叶子结点，你发现了么？这对任意n都是成立的哦。

因此这里我们就要从4开始不断的调用MAX-HEAPIFY(A,i)来构建最大堆。

为什么会有这一思路呢？

原因是既然我们知道了哪些结点是叶子结点，从最后一个非叶子结点（这里是4）开始，一次调用MAX-HEAPIFY函数，就会将该结点与叶子结点做相应的调整，这其实也就是一个递归的过程。

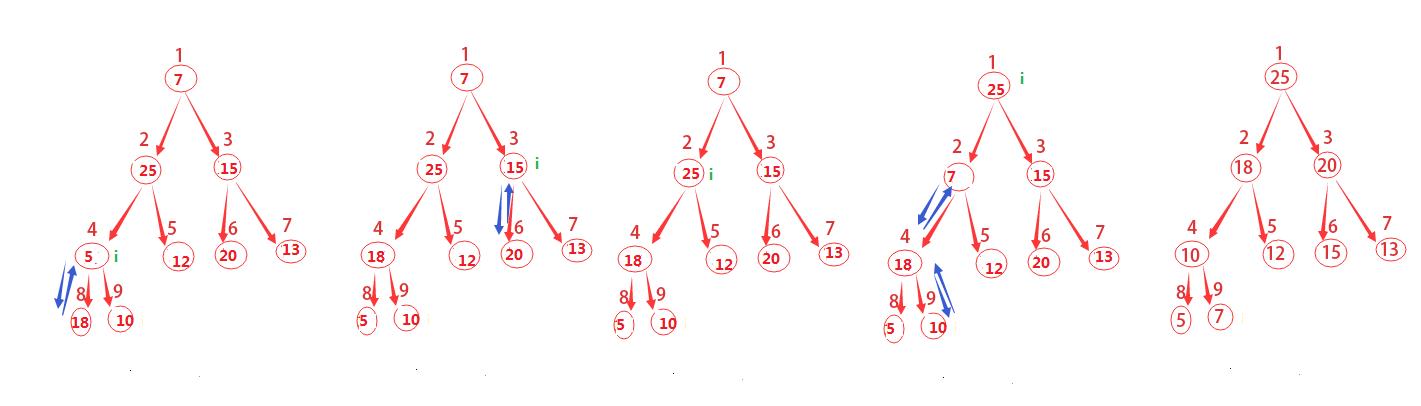
图示已经这么清晰了，就直接上伪代码咯。

BUILD-MAX-HEAP(A)
1   A.heap-size=A.length
2   for i=小于或等于A.length/2的最大整数 downto 1
3       MAX-HEAPIFY(A,i)

通过HEAPSORT进行堆排序算法

所谓的堆排序算法，先通过前面的BUILD-MAX-HEAP将输入数组 $A[1...n]$ 建成最大堆，其中 $n=A.length$ 。而数组中的元素总在根结点 $A[1]$ 中，通过把它与 $A[n]$ 进行互换，就能将该元素放到正确的位置。

如何让原来根的子结点仍然是最大堆呢，可以通过从堆中去掉结点n，而这可以通过减少 $A.heap-size$ 来间接的完成。但这样一来新的根节点就违背了最大堆的性质，因此仍然需要调用MAX-HEAPIFY(A,1)，从而在 $A[1...n-1]$ 上构造一个新的最大堆。

通过不断重复这一过程，知道堆的大小从 $n-1$ 一直降到2即可。

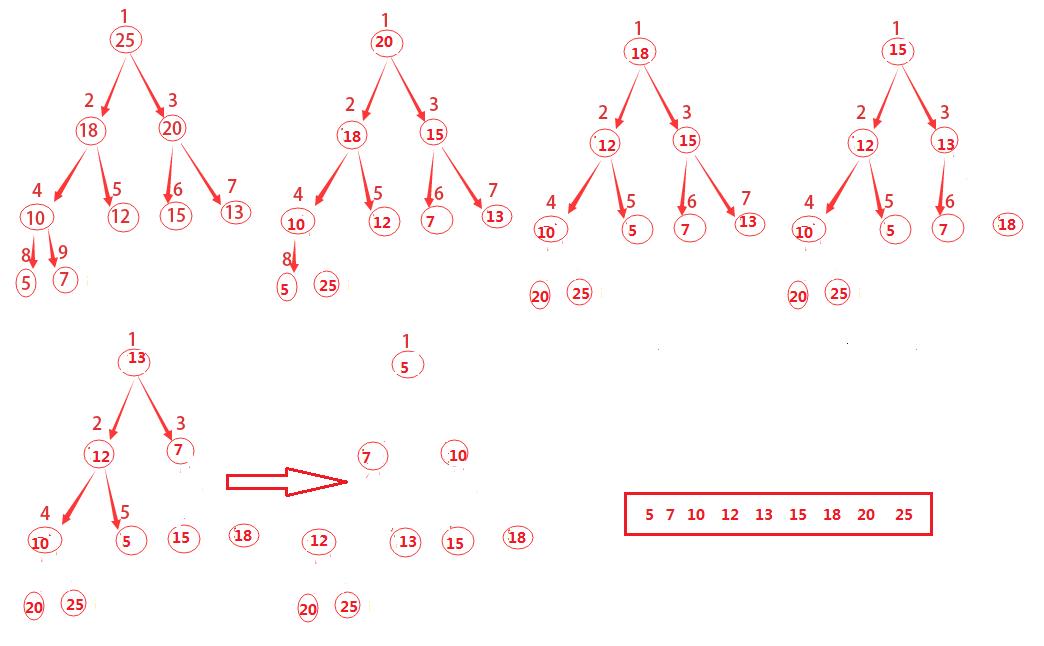
上图的演进方式主要有两点：

1）将 $A[1]$ 和 $A[i]$ 互换， $i$ 从 $A.length$ 一直递减到2

2）不断调用MAX-HEAPIFY(A,1)对剩余的整个堆进行重新构建

一直到最后堆已经不存在了。

HEAPSORT(A)
1   BUILD-MAX-HEAP(A)
2   for i=A.length downto 2
3       exchange A[1] with A[i]
4       A.heap-size=A.heap-size-1
5       MAX-HEAPIFY(A,1)

优先队列

下一篇博文我们就会介绍大名鼎鼎的快排，快速排序啦，欢迎童鞋们预定哦~

话说堆排序虽然性能上不及快速排序，但作为一个尽心尽力的数据结构而言，其可谓业界良心呐。它还为我们提供了传说中的“优先队列”。

优先队列（priority queue）和堆一样，堆有最大堆和最小堆，优先队列也有最大优先队列和最小优先队列。

优先队列是一种用来维护由一组元素构成的集合S的数据结构，其中每个元素都有一个相关的值，称之为关键字（key）。

一个最大优先队列支持一下操作：

$MAXIMUM(S)$ ：返回 $S$ 中有着最大键值的元素。
$EXTRACT-MAX(S)$ ：去掉并返回 $S$ 中的具有最大键字的元素。
INCREASE−KEY(S,x,a)详细图解Netty Reactor启动全流程 | 万字长文 | 多图预警