高精度点云配准 (最优传输角度上篇)
Posted 等待破茧
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了高精度点云配准 (最优传输角度上篇)相关的知识,希望对你有一定的参考价值。
目录
第一部分:点云配准的现状
第二部分:最优传输简介
第三第四部分:
这篇文章[English Version]主要是对点云配准方法谈下自己的认知,当然水平有限,欢迎指正。因为是简介所以涉及的数学不会很深,所以对于点云配准有兴趣的同学都欢迎阅读。
毕竟传统点云匹配的教程已经很齐全了(大家自行搜索啊!), 这里我们换个角度,主要从最优传输(optimal transport) 的角度展开对各种点云配准任务的讨论, 如果是学术方向的小伙伴可以参考 这里 了解更多的细节,另外若是引用本文图片也请参照这个链接。
至于为什么从最优传输(OT)相对复杂的角度入手呢, 从实战角度上来说, OT确实很强!非常强! 能够高效(精度及速度)解决这个领域诸多已有的以及难以解决的问题。但很遗憾可能是OT本身比较理论,并没有被很广泛的关注。 另外可能OT求解效率质的提升也是近两年的事情。总之OT对于点云配准这个任务来说,特别是场景流,刚性变换这些场景,以后是可以部分取代ICP成为新的通用工具的。 我们在很多类型的任务中观察到远胜于ICP的精确度和速度。 当然OT 也不是万能的,想要体现它的全部战力,我们也会引入一些其他概念来针对不同的任务环境。我们这里会涉及一些简单的任务比如 rigid 刚体配准,也会涉及一些复杂的任务 大规模(>100K points) 大形变点云配准。
本文安排如下
- 点云配准的现状
- 最优传输简介
- 形变模型(deformation model)
- 高精度点云配准
在进入正题之前我们先看看一些demos吧 :)!
肺部血管树点云匹配(呼气-> 吸气)
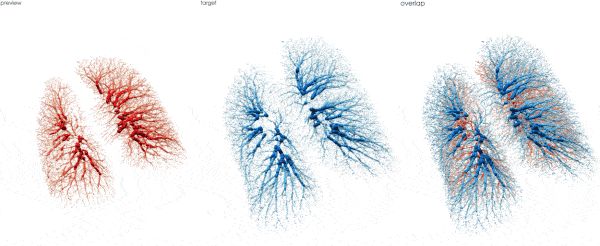
形状转换

场景流

局部刚性配准
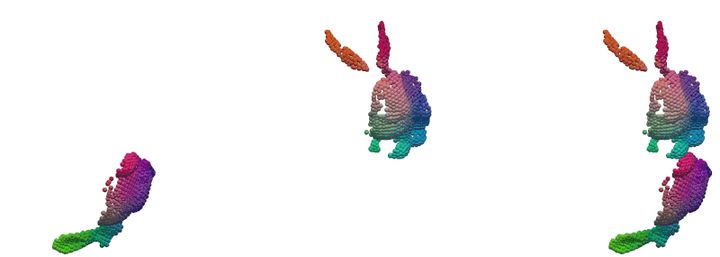
言归正传 :)
第一部分:点云配准的现状
点云配准的概念
这里我们先简单补充下点云配准的概念: 寻找一个几何变换 transformation,使source point set 在变换后和target point set相似.
我们拆解这个概念,可发现点云配准的核心有两个点 1. 如何寻找 source 和 target 的对应关系 2. 如何利用这个对应关系求解特定的变换 (transformation) 。
这里如何寻找对应关系隐性的利用到了相似性的概念,直观来说就是特征匹配:用source 中的点去匹配target 中的点,并计算它们的特征相似度。
业界现状
在进入具体讨论之前,我想简单概述下业界现状,希望对刚接触这个方向的同学有用,当然欢迎指出问题。
先说传统流吧
现在工业界貌似还是 Iterative Closest Point (ICP) 的天下,ICP 的核心思想就是: 1)寻找当前的source point 在target set 中的最近点, 从而确定其source 和target 的对应关系 2) 以此求解变换(通常是刚性或者 regularized 过的位移变换) 3) 对1) 和 2) 反复迭代。另外一个相似的主流方法是Coherent Point Drift (CPD), 其实是Bayes 下soften 的 ICP, 这里就不展开了。
- 岔开去点, 其实刚性变换, 特别是在partial 场景下如果feature 还凑合的话, feature matching 加 Teaser++ 其实挺够用的。
再说说学术流吧
学术界近些年有很多和deep learning 结合的工作, rigid 方向做的挺好的了, scene flow 场景流最近效果提升的也挺快的。之后可能在occlusion 场景,模型简化和范化上的工作会比较有吸引力。但整体而言,现在任务难度有限,并没有解决一些真实场景和复杂场景下(大规模,大形变,复杂结构)的点云匹配问题。这里涉及到三个问题 1) 首先暂时还没有这个类型的复杂公开数据集去刺激这个方向 2)学术界侧重idea,对传统 tensorflow, pytorch 的依赖比较明显只能在小规模点云上设计算法, 没有特别重视大规模的点云匹配问题。3)对deformation model 并没有足够的重视,一些复杂场景 不同的deformation model 的选择很重要。
针对与第一个问题 我们最近会公开一个含有1010 pairs 从呼气和吸气状态的CT图像提取的肺部点云的数据集,希望对这个方向未来的算法测试有所帮助。 第二个问题,不是做广告,但我这里比较推荐一个适合学术界的解决方案 Keops. 关于第三点,我会在下面的讨论中涉及一下初步的一些概念。
以上还是一些评论性内容,下面我们正式进入到方法的讨论。
第二部分:最优传输简介
首先我们来聊聊为什么用最优传输, 它的优劣各是什么。
OT的本质是全局匹配,惯例先看一个直观例子。
这里我们分别用 Nearest Neighbor 和 OT 来匹配一对树状结构
(严谨的来说这里我加了后期的smooth 来regularize transformation, 但在这里不是重点)
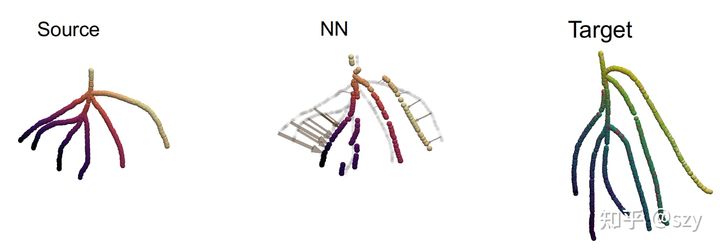
Fig 2.1. NN tree registration.
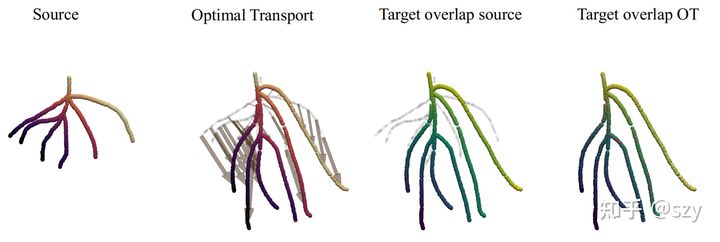
Fig 2.2. OT tree registration.
上面是 NN 的结果, 不出意料被 local trap 了,因为它是对每个source point 匹配target中的最近点, 下面是OT的结果,它用到了全局信息所以匹配的很好。
为了接下来的表述方便我们简单引入一些标记:
我们定义一个source 点云 ( ), iЄ1,...N 和一个 target 点云 ( ), jЄ1,...M。
这里 和 是欧式坐标,我们的点云是有权重的, 是 的权重, 是 的权重, 代表每个点的重要性,正常场景中可以设置为uniform。另外 和 这里指代的是对应点的特征向量。

Fig.2.3. Optimal transport.
在最优传输中,每个点的权重可以被理解成每个点的质量。 我们要把source set 中的质量转移到 target set 中。每一个 source point 都可以将它的质量分配给多个target points. 这里我们会定义一个cost function, 用来计算从一个source position传送单位质量 到 target position 需要花费多少的代价。 这里的cost function 定义很重要,直接决定了OT的策略。 最简单的就是利用欧式距离的平方 代表几何意义上的距离,但一般我们更通常使用feature 空间的距离 。一旦这些都定义好了,我们希望寻找一个最优传输方案 transport plan , 能够以尽可能小的代价把source set 中的质量都tranpsport 到target set 中去。
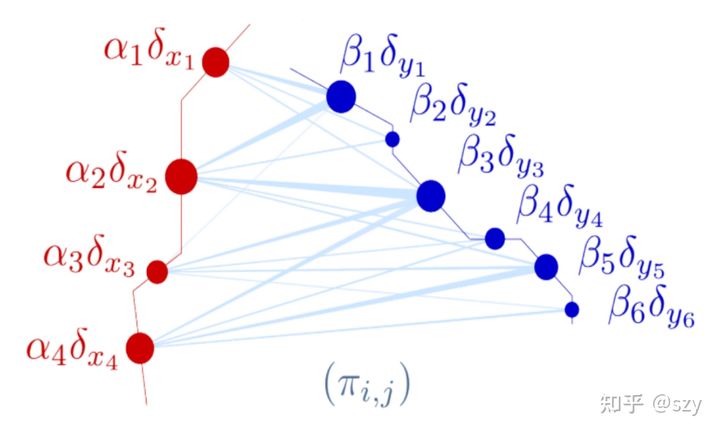
Fig.2.4. Transport plan.
现在我们来引入 Robot Optimal Transport (RobOT)(严格的说 这是 Entropic 和 unbalanced 形式下 optimal transport)。 这里引入它的主要目的是因为在正常场景中,我们无法保证source 和 target set 有相同的总质量。这里我们简单的看下RobOT的公式(并不需要完全理解)。

Fig.2.5. RobOT formulation.
这个公式可以拆分成三个部分, 第一个部分(蓝框)是我们之前说的transport cost. 第二个部分(绿框)是 一个entropic regularization 项。 第三个部分(黄框)是一个质量的regularization 项,鼓励传输过程中的质量能够守恒。这里只需要理解两个regularization 项前的参数 和 ,它们都是有很强的几何意义。、
具体而言。 我们通常称 为 blur, 因为它决定了变换transformation 的“分辨率”。

Fig.2.6. Illustration of blur.
我们通常称 为 reach, 因为它决定了soften upper bound, 当source 和 target 的feature 距离超过 时这两者之间不存在关联(匹配)。
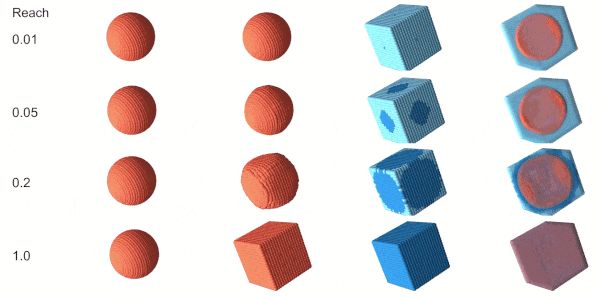
Fig.2.7. Illustration of reach. 这里sphere 和 cube 都在 [-1,1]之间,从左到右是source, deformed, target(深蓝表示接收到了来自source 的mass, overlap)
这里我们有个paritial rigid registration的例子, 通过调节reach, 我们能够将transport plan 类比成attention map.(内容长度原因,具体求解细节这里就不给出了)

Fig.2.8. Attention mechanism in RobOT.
其实到现在为止,我们一直在讨论OT/RobOT 本身,并没有给出怎么从transport plan 的求解问题 转换到registration的transformation问题。
我们之前提到过,在transport plan 中每一个source 都可以将质量分配给多个 target,但这并不是我们配准任务需要的,在配准中我们希望每个source 都能明确地移动到一个位置。所以这里我们引入 Weighted RobOT Matching, 具体是通过计算 target set 在 加权下的barycenter ,得到加权后的目标位置。

Fig.2.9. Weighted RobOT Matching.
到这里为止,我们简单的描述了如何利用RobOT 直接求解配准问题。没有引入其他的regularization 项,但这种解决方案并不是完美的。我们来看个例子, 这里目标是把彩色月亮匹配到蓝色月亮上去,我们简单的采用xyz作为每一个点的特征。 虽然形状匹配的很好,但很明显它的拓扑结构乱了。这是因为RobOT本身并没有regularize transformation, 这个在有较大rotation 的情况下非常明显。
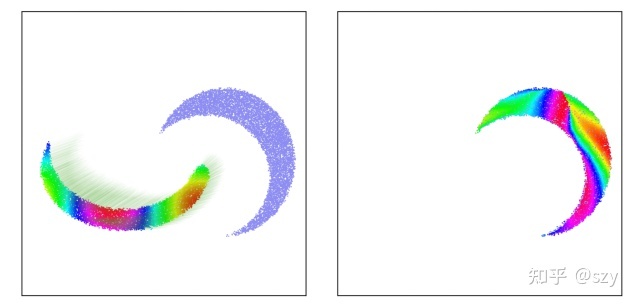
Fig.2.10. Please refer to Figure 3.31, F. Jean, Geometric data analysis, beyond convolution, 2021
到这里关于最优传输和点云配准的基础应用部分已经讲完了。我们看到了RobOT在点云配准中的优势也看到了它的不足。后面的部分我会着重强调如何引入deformation model 来弥补这些不足,以及如何将其结合深度学习运用到各种场景的任务中去。
第三第四部分:
考虑到内容篇幅和独立性原因, 第三第四部分单独更新了,见 高精度点云配准(最优传输角度下篇)
GitHub - uncbiag/shapmagn: shape registration 看我!
以上是关于高精度点云配准 (最优传输角度上篇)的主要内容,如果未能解决你的问题,请参考以下文章