强化学习入门笔记

Posted 2022-07-12 孤独腹地

强化学习

相关概念

我们先回忆一下童年，来看看超级玛丽这款游戏

在这款游戏里面的，我们需要控制超级玛丽进行左右行走、跳、攻击等动作，来躲避或攻击小动物、吃金币以及各种类型的增益道具。最终，获得的金币数量的多少以及通关代表我们玩游戏玩的好不好。

那么，如果我们希望让机器来玩这个游戏呢？怎么能让机器在合适的时候做出合适的动作？这就是强化学习要学的东西。

模型表示

在强化学习中，我们把超级玛丽称作智能体（Agent），而把游戏机制称作环境（Environment），把每一帧画面称作状态（State），把超级玛丽的行为称为动作（Action），把获得的金币数量或者通关称为奖励或回报（Reward）

我们玩一局超级玛丽开始的画面是固定的，这叫初始状态。我们根据状态选择执行合适的动作，这叫策略，通常表示为$\pi (a|s)$。通常策略分为随机性策略和确定性策略，随机性策略即$a\sim \pi (a|s)$，确定性策略即$a=\pi (s)$。

执行动作之后，游戏画面更新，这个过程叫做状态转移。当游戏失败或通关时，到达终止状态。

所以一局游戏就是给定初始状态下，不断地发生状态转移直到到达终止状态的过程。我们把这整个过程叫做马尔科夫决策过程，并且我们把从初态到终态的其中一种可能的序列称为一条轨迹。即 $\tau =s_0,a_0,r_1,s_1,a_1,r_2,s_2,...,s_T$

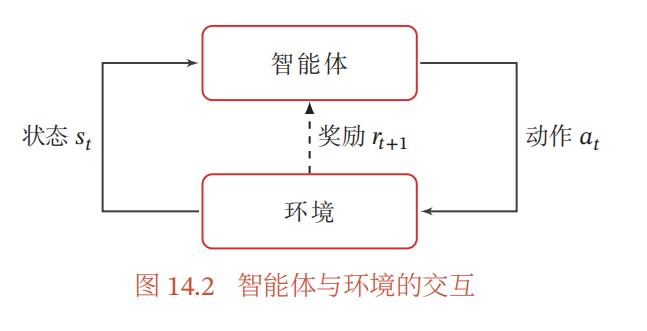
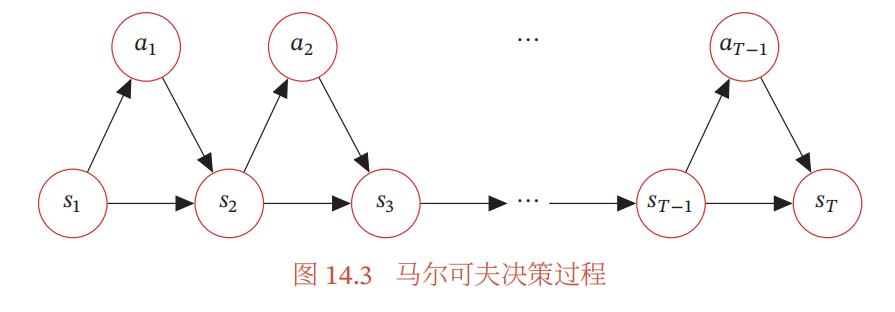
从图上我们可以看出所谓的马尔科夫决策过程就是一个有向图模型，回报是我们附加的用于训练的概念，它本质上与模型无关，通常是当前状态和动作的函数，因此不参与有向图的概率分解。

因此我们可以对马尔科夫决策过程的一条轨迹进行建模
$$p(\tau )=p(s_0)\prod _{i=0}^{T-1}\pi (a_i|s_i)\ast p(s_{i+1}|s_i,a_i)$$
这就是强化学习的模型表示。

目标函数

从机器学习的三要素出发，在明确模型之后，我们应该考虑学习准则或者叫目标函数。

强化学习中，要评估策略的好坏，跟奖励有关。

当我们根据策略做出一个动作后，我们可以根据即时奖励来评估动作的好坏
$$G_t=r_{t+1}$$
但这样我们或许就成了短视的人，只能看到当前的好处，看不到大局。因此，另一个方案是采用从该时刻开始到游戏结束时的累计奖励作为评估标准，这样我们就能纵观全局，考虑了当前动作对未来的深远影响。
$$G_t=r_{t+1}+r_{t+2}+...+r_T$$
但是这样也有问题，有的时候后期的奖励跟我们当前的动作其实并没有太大联系，我们加上后期奖励之后反倒有可能产生错误的评估结果。因此出现了一种折中的办法，即增加折扣率
$$G_t=r_{t+1}+\gamma r_{t+2}+{\gamma }^2{r}_{t+3}+...{\gamma }^{T-1}{r}_T$$
我们可以看到，当$\gamma$为0时，为第一种情况，$\gamma$为1时，为第二种情况，$0<\gamma <1$时，即为折中的办法，可根据现实情况自由调整。

因为策略和状态转移都有一定的随机性，所以每次试验得到的轨迹是一个随机序列，其收获的总回报也不一样。强化学习的目标是学习到一个策略${\pi }_{\theta }(a|s)$来最大化期望回报（Expected Return），即希望智能体执行一系列的动作来获得尽可能多的平均回报。
$$J(\theta )={\mathbb{E}}_{\tau \sim p_{\theta }(\tau )}[G(\tau )]={\mathbb{E}}_{\tau \sim p_{\theta }(\tau )}[G_0]={\mathbb{E}}_{\tau \sim p_{\theta }(\tau )}[\sum _{t=0}^{T-1}{\gamma }^t{r}_{t+1}]$$
为什么最大化期望回报就能作为强化学习的目标？

显然不同的轨迹导致不同的结果，我们希望回报越大的轨迹对应的概率越大，反过来，如果回报大的轨迹对应的概率小，那么得到的期望回报就越小。因此，最大化期望回报就会使得学习出来的模型会尽可能让大回报的轨迹更可能发生。

值函数

对我来说，值函数并不是先验的概念。我的意思是，前面所介绍的概念都是在定义强化学习时所必须的概念，不可或缺。但值函数确实在强化学习定义下，为了解决问题而导出的数学概念。

我们重新考虑期望回报的问题，虽然我们明确了强化学习的目标函数是期望回报，但并没有说如何计算它。显然如果直接按照期望的定义计算那是非常复杂的，因为我们根本不可能列出所有可能的轨迹。

于是贝尔曼通过动态规划的思想简化了它的计算问题

首先，
E τ ∼ p ( τ ) [ G ( τ ) ] = E s ∼ p ( s 0 ) [ E τ ∼ p ( τ ) [ ∑ t = 0 T − 1 γ t r t + 1 ∣ τ s 0 = s ] ] = E s ∼ p ( s 0 ) [ V π ( s ) ] \\large \\beginaligned \\mathbbE_\\tau \\sim p(\\tau)[G(\\tau)] &=\\mathbbE_s \\sim p\\left(s_0\\right)\\left[\\mathbbE_\\tau \\sim p(\\tau)\\left[\\sum_t=0^T-1 \\gamma^t r_t+1 \\mid \\tau_s_0=s\\right]\\right] \\\\ &=\\mathbbE_s \\sim p\\left(s_0\\right)\\left[V^\\pi(s)\\right] \\endaligned Eτ∼p(τ)​[G(τ)]​=Es∼p(s0​)​⎣⎡​Eτ∼p(τ)​⎣⎡​t=0∑T−1​γ强化学习笔记：随机高斯策略

gym强化学习入门demo——随机选取动作 其实有了这些动作和反馈值以后就可以用来训练DNN网络了

8万字Android Jetpack学习笔记，帮你快速入门强化实战

强化学习笔记：Gym入门--从安装到第一个完整的代码示例

强化学习入门笔记 | UCL silver RL | UC Berkely cs285 DRL

字节+谷歌超全Kotlin学习王炸笔记，Kotlin入门教程+高级Kotlin强化实战（附Demo）