递归：深度优先搜索

Posted 2022-06-27 我家大宝最可爱

二叉树的最大深度

二叉树的问题一般都是优先考虑递归的，我们想要求出一棵树的深度，当我们知道了左子树和右子树的深度的时候，那么root节点的深度就是左右子树最大的值加1
$$depth(root)=max(depth(root.left),depth(root.right))+1$$
很明显这也是一个递归的式子，所以直接使用递归即可

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        def dfs(root):
            if not root: # base case
                return 0
            l = dfs(root.left) # 先求左子树的深度
            r = dfs(root.right) # 然后求右子树的深度
            return max(l,r)+1 # 取最大，然后加上root节点就是+1
        return dfs(root)

二叉树的最小深度

一开始觉得最小深度和最大深度是一样的，但是发现直接写min是有问题的。

最重要的问题是，最小深度是从叶子节点开始的，所以base case有两种，一个是head==None，另一种就是head.right is None and head.left is None。必须是从叶子节点开始。

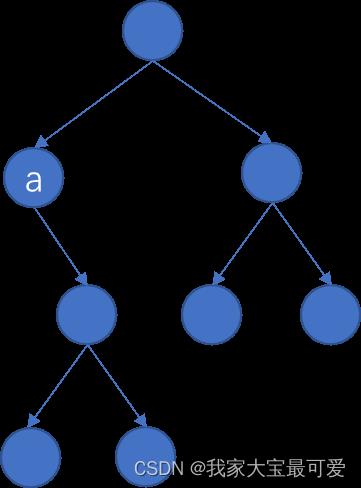
错误写法，可以看到a节点，a节点的左子树深度是0，右子树深度是2，那么根据这个错误的递归式子可以得到a节点的最小深度为min(0,2)=0，但是很明显，a节点不是一个叶子节点，所以不能求最小深度的。但是最大深度不会有这样的问题。

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0
        return min(self.minDepth(root.right),self.minDepth(root.left))+1

正确写法需要考虑某个子树为None的情况，这个时候需要递归另一边的子树作为最小深度。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0
        elif root.left is None and root.right is None:
            return 1
        elif root.left is None:
            return self.minDepth(root.right)+1
        elif root.right is None:
            return  self.minDepth(root.left) + 1
        else:
            return min(self.minDepth(root.right),self.minDepth(root.left))+1

平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1

这个问题本质也是求解树的深度，只不过要求左右子树的深度差值不超过1，如果超过一就会直接返回False。同样的理解，我们想要知道root节点是平衡的，那么就需要计算左右子树的高度，计算完高度之后，还需要判断左右子树是否也是平衡二叉树，如果有一个不是的话，那么root肯定也不是

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        def dfs(root):
            if not root:
                return 0,True
            l,lf = dfs(root.left)
            r,rf = dfs(root.right)

            if abs(l-r) <= 1 and lf and rf:
                return max(l,r)+1,True
            else:
                return max(l,r)+1,False
        
        _,f = dfs(root)
        return f

完全二叉树的节点个数

统计个数也是非常的简单，我们统计左子树的个数然后加上右子树的个数，然后加上根节点一个就是总共的节点个数了。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def countNodes(self, root: TreeNode) -> int:
        if root is None:
            return 0
        return self.countNodes(root.left) + self.countNodes(root.right) + 1