机器学习2 逻辑回归（Logistic Regression）

Posted 2022-06-23 拉风小宇

逻辑回归

首先谈一下我对这部分知识的理解，逻辑回归（西瓜书叫做对数几率回归）在这一部分主要是用于做分类的。
我们以一次考试为例，考试分为两门课，一共一百位同学参加考试，用黑色“+”表示通过，黄色“o”表示未通过，在二维坐标轴中将其表示出来

这是一个二分类问题，对于二分类来讲，最理想的就是“单位阶跃函数”了，$y(z)$在$z>0$的时候为1，在$z<0$时为0，在$z=0$时是0.5。但是单位阶跃函数的问题是他不连续，因此我们找到对数几率函数（logistic function）作为其替代函数，其在0附近有很大的变化率。我们可以认为在“大于0时为1，小于0时为0”，这样做二分类的效果是不错的。

sigmoid函数

在计算代价函数之前，首先回忆logistic回归假设由下式定义：
$$h_{\theta }(x)=g({\theta }^{T}x),$$
其中函数$g$是sigmoid函数，其中sigmoid函数由下式定义：
$$g(z)=\frac{1}{1+e^{-z}}$$
MATLAB实现如下

function g = sigmoid(z)
%SIGMOID Compute sigmoid functoon
%   J = SIGMOID(z) computes the sigmoid of z.

% You need to return the following variables correctly 
g = zeros(size(z));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the sigmoid of each value of z (z can be a matrix,
%               vector or scalar).
%g = (1/(1+exp(-z)));
for i=drange(1:size(z,1))
   for j=drange(1:size(z,2))
       g(i,j)=((1/(1+exp(-z(i,j)))));
   end
end

% =============================================================

end

代价函数和梯度

logistic回归中的代价函数为下式
$$J(\theta )=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}\log (h_{\theta }(x^{(i)}))-(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))]$$
并且代价函数的梯度是与$\theta$长度相同的向量，其中第$j$个元素由下面的式子进行定义：
$$\frac{\partial J(\theta )}{\partial {\theta }_j}=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$
这个公式看起来和线性回归的梯度公式是一样的，但是事实上却不同，因为线性回归和logistic回归对于$h_{\theta }(x)$是有不同的定义的。因此不能够用LMS的方法求解，但是可以用随机梯度下降的方法进行求解，代价函数和梯度计算的MATLAB程序如下

function [J, grad] = costFunction(theta, X, y)
%COSTFUNCTION Compute cost and gradient for logistic regression
%   J = COSTFUNCTION(theta, X, y) computes the cost of using theta as the
%   parameter for logistic regression and the gradient of the cost
%   w.r.t. to the parameters.

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;
grad = zeros(size(theta));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
%               You should set J to the cost.
%               Compute the partial derivatives and set grad to the partial
%               derivatives of the cost w.r.t. each parameter in theta
%
% Note: grad should have the same dimensions as theta
%
my = y.*(-1);
oy = 1.-y;
h = X*theta;
first = (1/m)*(my.*log(sigmoid(h)));
sec = (1/m)*oy.*log(1-sigmoid(h));
J = sum(first-sec);
grad = (1/m)*(X'*(sigmoid(h)-y));

% =============================================================
end

同样的，我们需要求出代价函数的最小值从而求得$\theta$值。我们这里直接利用MATLAB给出的内置函数来求解

%% ============= Part 3: Optimizing using fminunc  =============
%  In this exercise, you will use a built-in function (fminunc) to find the
%  optimal parameters theta.

%  Set options for fminunc
options = optimset('GradObj', 'on', 'MaxIter', 400);

%  Run fminunc to obtain the optimal theta
%  This function will return theta and the cost 
[theta, cost] = ...
	fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);

% Print theta to screen
fprintf('Cost at theta found by fminunc: %f\\n', cost);
fprintf('theta: \\n');
fprintf(' %f \\n', theta);

得到$\theta$的值为

theta =

  -24.9329
    0.2044
    0.1996

因此${\theta }^{T}x$为$-24.9329+0.2044x_1+0.1996x_2=0$
在这条线的上方，大概率应该是通过了的，在下方则认为是没有通过的

可以通过代码或者肉眼也可以看出有89个点是落在应该落在的区域中，分类效果还是蛮好的。

正规化逻辑回归

这一部分的例子相对于上一部分更加复杂一些，假设你是一个元器件厂的经理，每一个元器件需要经过两个测试，然后用黄色圆点表示不合格产品，而用黑色“+”表示合格品。用下图表示

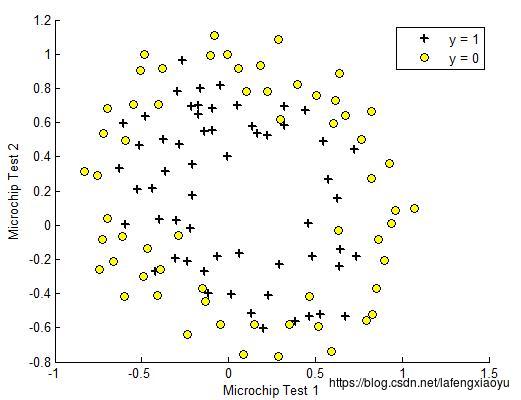
这个模型用刚才的方法显然就不合适了，需要进行特征映射

特征映射

我们这里提出的方案是将特征$x_1$和$x_2$映射入一个六次多项式
$$mapFeature(x)=\left[\begin{array}{c}1\\ x_1\\ x_2\\ x_1^2\\ x_1{x}_2\\ x_2^2\\ x_1^3\\ ⋮\\ x_1{x}_2^5\\ x_2^6\end{array}\right]$$
这就将二维特征的向量转换为28维的向量。在这个更高维度的特征向量上做logistic回归在二维中绘制将会有更复杂的边界。
映射函数如下

function out = mapFeature(X1, X2)
% MAPFEATURE Feature mapping function to polynomial features
%
%   MAPFEATURE(X1, X2) maps the two input features
%   to quadratic features used in the regularization exercise.
%
%   Returns a new feature array with more features, comprising of 
%   X1, X2, X1.^2, X2.^2, X1*X2, X1*X2.^2, etc..
%
%   Inputs X1, X2 must be the same size
%

degree = 6;
out = ones(size(X1(:,1)));
for i = 1:degree
    for j = 0:i
        out(:, end+1) = (X1.^(i-j)).*(X2.^j);
    end
end

end

当然值得一提的是，过拟合的现象是会因为维度提高发生的，因此我们需要想办法去克服。

代价函数和梯度

在正规化的logistic回归中的代价函数是
J ( θ ) = 1 m ∑ i = 1 m [ − y (