第二节4:K-Means算法及其Python实现(初始中心点的选择和K-Means++算法)
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第二节4:K-Means算法及其Python实现(初始中心点的选择和K-Means++算法)相关的知识,希望对你有一定的参考价值。
文章目录
一:朴素方法
最基本的 K K K- M e a n s Means Means算法在选取初始中心点时,采用的是随机选取的方法,但是这种方法很容易使算法陷入局部最优解,无法得到全局最优
- 比如可能会将两个较小的簇识别为一个簇,却将一个大的簇分别的情况

解决方法主要有以下三种
方法一:取一个数据集,首先采用层次聚类技术对它进行一个预聚类分析;之后从聚类的结果中提取出 k k k个簇,并计算这些簇的中心点作为 K K K- M e a n s Means Means算法的初始中心点;最后利用这些中心点初始化 K K K- M e a n s Means Means对原数据集进行聚类。这种方法可以很好解决初始点指派不合理问题,但仅在以下两种情况中奏效
- 数据集相对较小
- k k k的值相对于数据集来说较小
方法二:从数据集中随机抽取一些子样本集合,对每一个子样本集都实施随机选取初始中心点的 K K K- M e a n s Means Means算法;将算法运行后产生的中心点放到一个集合中,构成一个仅由中心点构成的集合;对这些集合进行聚类分析,将得到的结果作为原数据集初始化的中心点
方法三:采用最近邻密度的观点。此种方法建议选取那些邻域内有大量数据并且相互之间分散开的点作为初始中心点的候选点集,平均的配对欧氏距离可通过下式计算得到
d 1 = 1 N ( N − 1 ) ∑ i = 1 N − 1 ∑ j = i + 1 N ∣ ∣ x i − x j ∣ ∣ d_1=\\frac1N(N-1)\\sum\\limits_i=1^N-1\\sum\\limits_j=i+1^N||x_i-x_j|| d1=N(N−1)1i=1∑N−1j=i+1∑N∣∣xi−xj∣∣
在选取了第一个中心点后,每个初始中心点的选取都要同时考虑到其周围点的密度以及该点与之前选取的所有点的分散度
二: K K K- M e a n s Means Means++算法
- 该算法有效解决了关于初始值的选取问题,目前已经成为了一种硬聚类算法的标准
(1)算法思想
K K K- M e a n s Means Means++算法:该算法在选取初始中心点时的关键点是初始的聚类中心点之间的距离要尽可能远,这样就可以充分考虑到数据样本集内的所有样本的分布情况。具体来说,算法首先会随机选取一个初始中心点,之后选取距离这个中心点最远的点作为下一个初始点,然后重复这种选取方式直到 k k k个中心点全部选取完成。但是这样做最大的问题就是会受到离群点的干扰,所以在选取的过程中要引入一个概率的思想,将每个点被选中的概率与其距最近的已选中心点的距离相互联系,距离越大,被选取为聚类中心点的概率也就越大
(2)算法流程
如下是算法流程,核心之处在于
- 先计算每一个非中心点与其相距最近的中心点之间的距离 D ( x ) D(x) D(x)被加和得到 S u m ( D ( x ) ) Sum(D(x)) Sum(D(x))
- 选取的过程是取决于处于 S u m ( D ( x ) ) Sum(D(x)) Sum(D(x))中的一个随机值,然后用这个随机值减去每个距离 D ( x ) D(x) D(x)直至得到负值
- 选取过程结束,取这个距离对应的这个点作为下一个初始中心点

(3)Python实现
下面代码中,主体部分和 K K K- M e a n s Means Means算法一致,只不过多了如下两个函数
get_centorids(data_set, k):用于获取初始中心点nearest(point, centorids):用于计算样本点到各聚类中心最短距离
import numpy as np
import sys
import random
'''
1、在数据集中随机选择一个样本作为第一个初始化聚类中心;
2、计算样本中每一个样本点与已经初始化的聚类中心的距离,并选择其中最短的距离;
3、以概率选择距离最大的点作为新的聚类中心;
4、重复2、3步直至选出k个聚类中心;
5、对k个聚类中心使用K-Means算法计算最终的聚类结果。
'''
# 计算最短距离
def nearest(point, centorids):
min_dist = sys.float_info.max
m = np.shape(centorids)[0] # 已经初始化的聚类中心个数
for i in range(m):
# 计算该点与每个聚类中心之间的距离
dist = np.sqrt(np.sum(np.power(point - centorids[i, ], 2)))
# 选择最短距离
if min_dist > dist:
min_dist = dist
return min_dist
# k-means++获取初始中心点
def get_centorids(data_set, k):
m, n = np.shape(data_set)
centorids = np.zeros((k, n))
# 1.随机选取一个样本点作为第一个聚类中心
index = np.random.randint(0, m)
centorids[0, ] = np.copy(data_set[index, ]) # 第一个聚类中心
# 2.初始化一个聚类序列
dist = [0.0 for _ in range(m)]
for i in range(1, k):
sum_all = 0
for j in range(m):
# 3.对每一个样本找到其最近的聚类中心点
dist[j] = nearest(data_set[j, ], centorids[0:i, ])
# 4.将所有的最短距离相加
sum_all += dist[j]
# 5.取一个位于sum_all之间的随机值
R = sum_all * np.random.random() # 随机值R
for j, di in enumerate(dist):
# 6.重复计算R=R-D(X)直到R小于等于0,此时的样本点可以作为聚类中心点
R -= di
if R > 0:
continue
centorids[i] = np.copy(data_set[j, ])
break
return centorids
# 计算距离实现划分
def compute_cluster(data_set, centorids):
examples_nums = np.shape(data_set)[0] # 样本数量
centorids_nums = np.shape(centorids)[0] # 质心数量
cluster = np.zeros((examples_nums, 1)) # 返回结果
for examples_index in range(examples_nums):
distance = np.zeros(centorids_nums) # 保存examples_index这个样本点到各质心点的距离
for centorids_index in range(centorids_nums):
distance[centorids_index] = np.sqrt(np.sum(
np.power(data_set[examples_index, :]-centorids[centorids_index, :], 2)))
cluster[examples_index] = np.argmin(distance) # 最终在这些距离中选择出最小的一个
return cluster
# 用于更新质心
def renew_centoids(data_set, cluster, k):
features_num = data_set.shape[1] # 特征格式,即属性
centorids = np.zeros((k, features_num)) # k个簇每个都要计算,且每个簇的点都有features_num个属性,所以要对应计算
for centroid_id in range(k):
closest_ids = cluster == centroid_id # 不懂的话可以查阅 “Numpy布尔数组”相关内容
centorids[centroid_id] = np.mean(data_set[closest_ids.flatten(), :], axis=0)
return centorids
# 算法主体
def k_means_plus(data_set, k, max_iterations):
examples_nums = np.shape(data_set)[0] # 样本数量
centorids = get_centorids(data_set, k) # 随机选取k个质心
cluster = np.zeros(examples_nums) # 用于标识该样本点与那个质心最近,其本质就是划分的簇
for _ in range(max_iterations): # 不断迭代
# 计算距离且分配
cluster = compute_cluster(data_set, centorids)
# 更新质心
centorids = renew_centoids(data_set, cluster, k)
return centorids, cluster
(4)分析
采用这种选取方法可以在一定程度上避免数据集中所包含的离群点对要选择相距最远的中心点目标的干扰,具体来说
- 相对于正常数据点,离群点所计算出的 D ( x ) D(x) D(x)一定较大,这样在选取的过程中,它被选中的概率也就越大
- 但在整个数据集中,离群点必定只占极小的一部分,大部分是正常的数据点,因此在数量上正常的数据点是有明显优势的
- 所以,离群点在概率上的优势在一定程度上会被正常数据点在数量上的优势给平衡掉,从而保证了整个算法的平衡
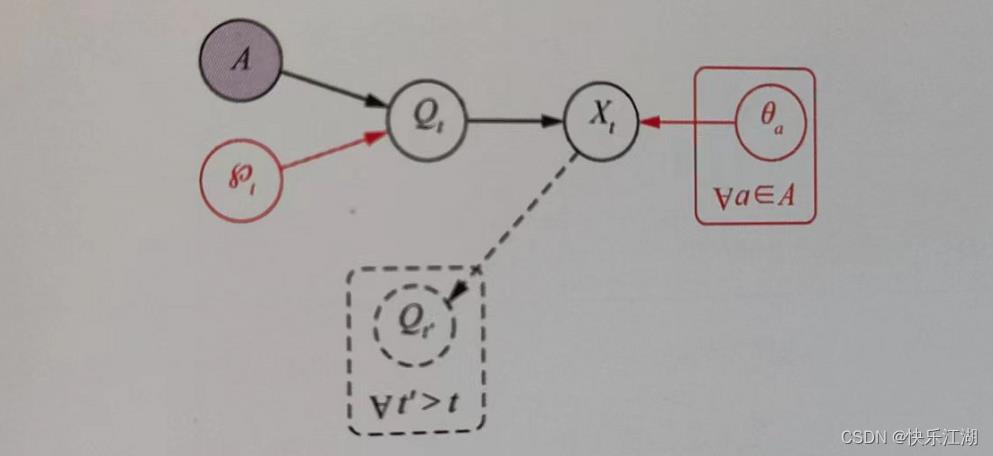
三: k k k- v a r i a t e s variates variates++算法
- k k k- v a r i a t e s variates variates++算法是 K K K- M e a n s Means Means++算法的一般化版本,它适用性很强;这里仅做了解,日后如有需要再做探讨
- 算法论文链接
算法流程如下
- 其中, u n u_n un表示在 A ( ∣ A ∣ = n ) A(|A|=n) A(∣A∣=n)上的均匀分布

下图是 k k k- v a r i a t e s variates variates++算法的理解
以上是关于第二节4:K-Means算法及其Python实现(初始中心点的选择和K-Means++算法)的主要内容,如果未能解决你的问题,请参考以下文章