随机共振基于随机共振的高灵敏度GPS信号捕获算法

Posted 2022-06-17 fpga和matlab

算法结构图

首先input输入到SR

这个语句意思就是每次输入一段数据进行处理，因为这个系统是实时反馈的系统，所以在处理的时候，必须是一段段处理，而不能和原来一样一次性进行处理，所以我们每次处理的数据长度为FLEN。

这个是FFT的频率反馈。

第一次迭代，由于没有得到FFT，所以设置为0，然后后面的根据反馈结果对新输入的数据进行修正。

51~66行，是采用龙哥库塔算法计算SR系统，龙哥库塔算法在具体公式：即

 然后开始稀疏处理，大概流程如下所示：

根据上述的过程，结合我们的程序，具体如下

首先初始化字典，不过这里，其中DCT矩阵使用cos表示。

第二、

这里，step为稀疏度，我设置的4，相当于用原来的step*step分之一来表示信号，这样就稀疏了。

具体你可以参考

中的

比较类似。

第三

我的代码就是

这个就是OMP过程。就不做介绍了。

第四

就是更新原子字典的过程。

对应程序是：

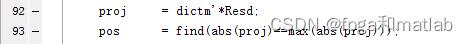
对应程序是：

然后，我这里更新的过程和他稍微不一样。

残差得到之后，下一次迭代的时候，使用Resd这个残差作为后一次迭代使用。

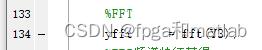
这里开始FFT变换

然后频谱特征的获得

最后是频率参数的获得

将估计得到的Fest反馈给前面的fd，进行多普勒频偏的修正

clc;
clear;
close all;
warning off;


LEN = 10000;

% load awgnsignal2.mat
% time2 = ans.Time;
% for i = 1:length(time2)
%     Xawgn(i,1)     = ans.Data(1,1,i);
% end
% save input.mat Xawgn time2

%以下数据从你的simulink中保存，2为-5db，3为-15db，4为-20db，5为-25db，6为-39db
% load input2.mat
% load input3.mat
% load input4.mat
% load input5.mat
load input6.mat
figure;
plot(time2(1:LEN),Xawgn(1:LEN));
title('噪声信号');
xlim([0,time2(LEN)]);
xlabel('t/s');
ylabel('Amplitude');

%信号的采样率
Fs    = 2.046e8;
%循环迭代过程中，每次输入的数据长度
FLEN  = 8192;
Xsave1= [];
Xsave2= [];

for jj = 1:30
    jj
    Inputs= Xawgn(FLEN*(jj-1)+1:FLEN*jj);
    %求解使用四阶Runge-Kutta方法
    %尺度变换SR
    %这里fd为反馈调整频率，用来修正多普勒频谱，初始输入阶段，fd设置为0.
    if jj == 1
       fd = 0; 
       x1 = real(Inputs(1:length(Inputs))*exp(-sqrt(-1)*2*pi*fd/Fs));
    else%fd为后端FFT之后从其频率谱中提取的特征
       fd = Fest; 
       x1 = real(Inputs(1:length(Inputs))*exp(-sqrt(-1)*2*pi*fd/Fs));   
    end
 
    %自适应调整参数a和h
    a0     = 1.8;
    a1     = 1.2;        
    b      = 0.05;%参数b固定，调整a和h
    h0     = 0.1;
    h1     = 0.08;
    x      = zeros(1,length(x1));
    for i=1:length(x1)-1
        %计算a changed
        a      = a0 + (a1-a0)/length(x1);
        h      = h0 + (h1-h0)/length(x1);
        k1     = h*(a*x(i)-b*x(i).^3+x1(i));
        k2     = h*(a*(x(i)+k1/2)-b*(x(i)+k1/2).^3+x1(i));
        k3     = h*(a*(x(i)+k2/2)-b*(x(i)+k2/2).^3+x1(i+1));
        k4     = h*(a*(x(i)+k3)-b*(x(i)+k3).^3+x1(i+1));
        x(i+1) = x(i)+(1/6)*(k1+2*k2+2*k3+k4);
    end
 
    xstage3       = x;
    xstage3(1:200)=[];
    xstage3 =xstage3-mean(xstage3);
    xstage3 =xstage3/max(abs(xstage3));
    %稀疏处理
    %rec_X2   = func_omp_denoise(xstage3);
    X0       = xstage3;
    X1       = [X0;X0;X0;X0;X0;X0;X0;X0];
    Vnoise   = 0.1;
    X1       = double(X1);
    X1_std   = std2(X1);
    [RR,CC]  = size(X1);
    N        = 32;
    C        = 1/(2*Vnoise^2*(1+Vnoise^2/X1_std^2));
    step     = 4;
    X2       = X1;
    X2       = imresize(X2,4);
    [RR,CC]  = size(X2);
    %字典
    K          = 32*32;                         
    dictmatrix = zeros(N,sqrt(K));                 
    for k=0:sqrt(K)-1
        V = cos((0:1:N-1)*k*pi/sqrt(K));
        if k>0 
           V=V-mean(V); 
        end
        dictmatrix(:,k+1)=V/norm(V);
    end;
    dictmatrix2 = kron(dictmatrix,dictmatrix);                          
    dictmatrix2 = dictmatrix2 * diag(1./sqrt(sum(dictmatrix2.*dictmatrix2))); 
    X3          = zeros(N*N, ceil(1/step*(RR-N+1))*ceil(1/step*(CC-N+1)));
    cnt = 0;
    for is = 1:step:RR-N+1
        for js = 1:step:CC-N+1
           cnt        = cnt + 1;
           tmps       = X2(is:is+N-1, js:js+N-1);
           X3(:, cnt) = tmps(:);
        end
    end

    %重构
    rec_dictmatrix = zeros(size(dictmatrix2, 2), cnt);

    for is = 1:cnt
        rec_dictmatrix(:,is) = func_omp(dictmatrix2, X3(:,is), Vnoise);
    end
    rec_X = dictmatrix2 * rec_dictmatrix;
    %重组
    [rec_X2, W] = func_Recon(rec_X, step, RR, CC, N);
    rec_X2      = rec_X2./W;

    %最后的平滑处理，
    Y2        = rec_X2(1,:);
    Y3        = Y2;
    KK        = 512;
    for is = 1:length(Y2)
        if is <= KK
           Y3(is) = mean(Y2(1:is)); 
        else
           Y3(is) = mean(Y2(is-KK:is));  
        end
    end
    Y3(1:KK/2)=[];
 
    FFTlen   = length(Y3);%处理数据长度， 也即FFT的长度，用来实时反馈频率估计值
    %FFT
    yfft     = fft(Y3);
    %FFT频谱特征获得
    yfft2    = fftshift(abs(yfft));
    %FFT频谱中提取频率参数调整，将频率估计值反馈到输入的数据中

    FF          = [0:FFTlen/2]/FFTlen*Fs;
    yfft3       = yfft2(FFTlen/2:end);
    [Vmax,Imax] = max(yfft3);
    Fest        = FF(Imax);%得到频率估计值，根据论文中介绍的自适应技术将频率估计结果反馈给
    
    %保存处理后的数据
    Xsave1= [Xsave1,Inputs'];
    Xsave2= [Xsave2,Y3];
end
   

Xsave1   = Xsave1/max(abs(Xsave1));
Xsave2   = Xsave2/max(abs(Xsave2));

%对比处理前后的信号的频谱
yfft1    = fft(Xsave1);
yfft1    = fftshift(abs(yfft1));FFTlen=length(yfft1);
FF1      = [-FFTlen/2+1:FFTlen/2]/FFTlen*Fs;
yfft2    = fft(Xsave2);
yfft2    = fftshift(abs(yfft2));FFTlen=length(yfft2);
FF2      = [-FFTlen/2+1:FFTlen/2]/FFTlen*Fs;
    


figure;
subplot(211);
plot(Xsave1);title('处理前的噪声信号');
xlim([0,1.5e5]);
subplot(212);
plot(FF1,yfft1);title('信号频谱'); 
ylim([0,2000]);

figure;
subplot(211);
plot(Xsave2);title('处理后的信号');
xlim([0,1.5e5]);
subplot(212);
plot(FF2,yfft2);title('信号频谱'); 
% ylim([0,20000]);

仿真结果如下：

A28-75