剑指offer(C++)-JZ33：二叉搜索树的后序遍历序列(数据结构-树)

Posted 2022-05-26 翟天保Steven

作者：翟天保Steven
版权声明：著作权归作者所有，商业转载请联系作者获得授权，非商业转载请注明出处

题目描述：

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回 true ,否则返回 false 。假设输入的数组的任意两个数字都互不相同。

数据范围： 节点数量 0≤n≤1000 ，节点上的值满足 1≤val≤105 ，保证节点上的值各不相同
要求：空间复杂度 O(n)，时间时间复杂度 O(n^2)

提示：

1.二叉搜索树是指父亲节点大于左子树中的全部节点，但是小于右子树中的全部节点的树。

2.该题我们约定空树不是二叉搜索树

3.后序遍历是指按照 “左子树-右子树-根节点” 的顺序遍历

4.参考下面的二叉搜索树，示例 1

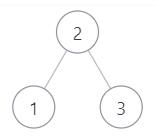
示例1：

输入：

[3,1,2]

返回值：

false

说明：

不属于上图的后序遍历，从另外的二叉搜索树也不能后序遍历出该序列 ，因为最后的2一定是根节点，前面一定是孩子节点，可能是左孩子，右孩子，根节点，也可能是全左孩子，根节点，也可能是全右孩子，根节点，但是[3,1,2]的组合都不能满足这些情况，故返回false  

示例2： 

输入：

[5,7,6,9,11,10,8]

返回值：

true

解题思路：

本题考察数据结构树的使用。两种解法：

1）递归法。二叉树的后序遍历顺序是左右根，最后一个结点是根，往前大于根值的都是右子树的范畴，再往前小于根植的都是左子树。基于上述逻辑，可以拆解左右子树，再对左右子树分别检查，直到最深层完成，再一层层返回结果，完毕。

2）模拟检验法（栈）。二叉搜索树的中序遍历序列和从小到大排序序列一致，因此可以快速获取中序遍历序列；将中序遍历序列入栈，模拟后序遍历序列的出栈行为，若合理，则说明是二叉搜索树的后续遍历结果。

测试代码：

解法一：递归法

class Solution 
public:
    bool VerifySquenceOfBST(vector<int> sequence) 
        int size=sequence.size();
        if(size==0)
            return false;
        return check(sequence,0,size-1);
    
    
    bool check(vector<int> sequence, int start, int end)
    
        // 当start和end重合，返回true
        if(start>=end)
            return true;
        // 获取根结点
        int root=sequence[end];
        // 获取右子树
        int j=end-1;
        while(j>=0&&sequence[j]>root)
            j--;
        // 分析左子树
        for(int i=start;i<=j;++i)
        
            if(sequence[i]>root)
                return false;
        
        // 左右子树分别检查
        return check(sequence,start,j)&&check(sequence,j+1,end-1);
    
;

 解法二：模拟检验法（栈）

class Solution 
public:
    bool VerifySquenceOfBST(vector<int> sequence) 
        if(sequence.empty()) 
            return false;
        // 获取中序遍历序列
        // 二叉搜索树的中序遍历序列和其从小到大排序结果一致
        vector<int> midorder(sequence);
        sort(midorder.begin(), midorder.end());
        // 模拟中序遍历和后续遍历，验证所对应的二叉搜索树是否一致
        return getResult(midorder, sequence);
    
 
    bool getResult(vector<int> midorder,vector<int> sequence) 
         int s = midorder.size();
         // 定义栈
         stack<int> temp;
         int i = 0, j = 0;
         // 遍历midorder（中序遍历序列）
         while(i < s)
         
             // 将中序遍历序列的值依次入栈
             temp.push(midorder[i]);
             // 模拟后序遍历序列的出栈序列
             while(!temp.empty() && temp.top() == sequence[j])
             
                 ++j;
                 temp.pop();
             
             ++i;
         
        // 判断是否匹配
         return j == s;
     
;