Simulation | Multi-Armed Bandit Algorithm

Posted 2022-05-06 Rein_Forcement

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Simulation | Multi-Armed Bandit Algorithm相关的知识，希望对你有一定的参考价值。

Simulation | Multi-Armed Bandit Algorithm

I. Propose

$\\bullet$ Simulation of Multi-Armed Bandit Algorithms: $\\varepsilon$ -Greedy, UCB(Upper Confidence Bound), Thompson Sampling and Gradient Bandit Algorithm.

$\\bullet$ Compare the algorithms with different parameter and give explanation for these impact.

$\\bullet$ Explain the understanding of the exploration-exploitation trade-off in bandit-algorithms.

$\\bullet$ Solve the further problem: dependent case.

$\\bullet$ Explain why sublinear regret is the performance threshold between good bandit algorithms and bad one.

II. Simulation

Step 1: Oracle Value of Bernoulli Distribution

Suppose we have known the true values of the parameters of the Bernoulli Distribution $\\theta_j )$ of each arm (the probability of each bandit gives a reward) as below:

$\\theta_1 = 0.9,\\theta_2 = 0.8,\\theta_3 = 0.7$

We can use the parameters above to compute the expectation of aggregate rewards of each arm over N=10000 times slots, which can be achieved by testing Bin( $N$ , $\\theta_j$ ) .

The test function with parameters $\\theta_j$ is as below:

import math
import random
import numpy as np
from collections import Counter
import matplotlib.pyplot as plt
from scipy.stats import beta

def oracle(N,theta):
    # experiments of bin(n, theta)
    arm = np.random.binomial(1,theta,N)

    #output the total times of success
    return Counter(arm)[1]

The test function above outputs the total successful times of Bern( $\\theta_j$ ) over $N$ times slots. Then we can use the function to compute the theoretically maximized expected rewards (oracle value).

The result is as below:

def Oracle(arm_mean,N):

    #first arm with theta_1 = 0.8
    arm_1 = oracle(N,arm_mean[0])

    #second bandit with theta_2 = 0.6
    arm_2 = oracle(N,arm_mean[1])

    #third bandit with theta_3 = 0.5
    arm_3 = oracle(N,arm_mean[2])

    #compute the maximum of the expectation of three bandits
    arm = np.array([arm_1,arm_2,arm_3])
    max_i = np.argmax(arm)
    maximum = max(arm_1,arm_2,arm_3)

    return maximum,max_i

arm_mean = [0.9,0.8,0.7]
N = 10000

oracle_value,max_i = Oracle(arm_mean,N)
print("The oracle value is , from arm .".format(oracle_value,max_i+1))

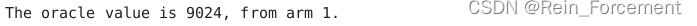
From the result, we can find if we have known the probability of success of each arm: $\\theta_j$ , it is obvious to choose the bandit with the maximized probability to get the theoretically maximized aggregate expectation, which is the oracle value.
To test the performance of these algorithms, firstly we generate a function named run_algorithm to run these three algorithm. The final ouput is arrays that record the mean of average reward and cumlative reward after each experiment with $N = 5000$ slots.

def run_algorithm(algo, arms, num_exper, num_slot):
    
    #initialize the arrays record the rewards and chosen arms
    rewards = np.zeros((num_exper,num_slot))
    chosen_arm = np.zeros((num_exper,num_slot))

    for exper in range(num_exper):
        
        #initialize the algorithm
        algo.initialize(len(arms))
        
        for slot in range(num_slot):
            
            #obtain the factor of update
            arm = algo.best_arm()
            reward = arms[arm].draw()

            #update the data
            chosen_arm[exper,slot] = arm
            rewards[exper,slot] = reward
            algo.update(arm,reward,slot)

    #compute the average and cumulation of rewards
    average_reward = np.mean(rewards,axis=0)    
    cumulative_reward = np.cumsum(average_reward)

    return chosen_arm,average_reward,cumulative_reward

Also, we need to generate a function named plot_algorithm to plot the output of each algorithm. And then we can compare the performance of each algorithm with different parameters by the plots.

def plot_algorithm(algo_name, para, arms, arm_mean, num_exper, num_slot, label):

    fig,axes = plt.subplots(2,2,figsize=[15,9])
    R = []
    Percentage = []
    optimal_arm = np.argmax(arm_mean)

    #Greedy and UCB
    if algo_name == Greedy or algo_name == UCB:
        for para in para:

            #run the algorithm
            algo = algo_name(para)
            chosen_arm,average_reward,cumulative_reward = \\
                run_algorithm(algo,arms,num_exper,num_slot)

            #plot the average reward
            axes[0][0].plot(average_reward,label=f"label = para")
            axes[0][0].set_xlabel("Slots")
            axes[0][0].set_ylabel("Average Reward")
            axes[0][0].set_title("Average Reward")
            axes[0][0].legend(loc="lower right")
            axes[0][0].set_ylim([0, 1.0])

            #plot the cumulative reward
            axes[0][1].plot(cumulative_reward,label=f"label = para")
            axes[0][1].set_xlabel("Slots")
            axes[0][1].set_ylabel("Cumulative Reward")
            axes[0][1].set_title("Cumulative Reward")
            axes[0][1].legend(loc="lower right")

            #regret part
            regret = np.zeros((num_exper,num_slot))
            average_regret = np.zeros(num_slot)
            optimal_num = np.zeros(num_slot)
            optimal_percent = np.zeros(num_slot)

            #calculate the regret
            for exper in range(num_exper):
                for slot in range(num_slot):
                    regret[exper,slot] = arm_mean[optimal_arm] - arm_mean[int(chosen_arm[exper,slot])]
                    if int(chosen_arm[exper,slot]) == optimal_arm:
                        optimal_num[slot] += 1
            optimal_percent = optimal_num/num_exper
            average_percent = np.mean(optimal_percent)
            average_regret = np.mean(regret,axis=0)
            total_regret = np.sum(average_regret)
            cumulative_regret = np.cumsum(average_regret)

            #plot the regret as a function of time
            axes[1][0].plot(cumulative_regret,label=f"label = para")
            axes[1][0].set_xlabel("Slots")
            axes[1][0].set_ylabel("Cumulative Regret")
            axes[1][0].set_title("Cumulative Regret")
            axes[1][0].legend(loc="lower right")

            #plot the optimal action percent as a function of slots
            axes[1][1].plot(optimal_percent,label=f"label = para")
            axes[1][1].set_xlabel("Slots")
            axes[1][1].set_ylabel("Percent")
            axes[1][1].set_title("Optimal action Selection")
            axes[1][1].legend(loc="lower right")
            axes[1][1].set_ylim([0, 1.0])

            #print the total regret accumulated over each experiment
            print(" = : The total regret accumulated is :.4f.".format(label,para,total_regret))

            #print the average percentage of plays in which the optimal arm is pulled 
            print(" = : The average percentage of optimal arm is pulled is :.4f.".format(label,para,average_percent))
            
            reward = cumulative_reward[num_slot-1]
            R.append(reward)
            Percentage.append(average_percent)

    #Thompson Sampling
    elif algo_name == TS:
        i = 1
        for para in para:

            #run the algorithm
            algo = algo_name(para[0],para[1])
            chosen_arm,average_reward,cumulative_reward = \\
                run_algorithm(algo,arms,num_exper,num_slot)

            #plot the average reward
            axes[0][0].plot(average_reward,label="beta"+str(i))
            axes[0][0].set_xlabel("Slots")
            axes[0][0].set_ylabel("Average Reward")
            axes[0][0].set_title("Average Reward")
            axes[0][0].legend(loc="lower right")
            axes[0][0].set_ylim([0, 1.0])
            
            #plot the cumulative reward
            axes[0][1].plot(cumulative_reward,label="beta"+str(i))
            axes[0][1].set_xlabel("Slots")
            axes[0][1].set_ylabel("Cumulative Reward")
            axes[0][1].set_title("Cumulative Reward")
            axes[0][1].legend(loc="lower right")

            #regret part
            regret = np.zeros((num_exper,num_slot))
            average_regret = np.zeros(num_slot)
            optimal_num = np.zeros(num_slot)
            optimal_percent = np.zeros(num_slot)

            #calculate the regret
            for exper in range(num_exper):
                for slot in range(num_slot):
                    regret[exper,slot] = arm_mean[optimal_arm] - arm_mean[int(chosen_arm[exper,slot])]
                    if int(chosen_arm[exper,slot]) == optimal_arm:
                        optimal_num[slot] += 1
            optimal_percent = optimal_num/num_exper
            average_percent = np.mean(optimal_percent)
            average_regret = np.mean(regret,axis=0)
            total_regret = np.sum(average_regret)
            cumulative_regret = np.cumsum(average_regret)

            #plot the regret as a function of time
            axes[1][0].plot(cumulative_regret,label="beta"+str(i))
            axes[1][0].set_xlabel("Slots")
            axes[1][0].set_ylabel("Cumulative Regret")
            axes[1][0].set_title("Cumulative Regret")
            axes[1][0].legend(loc="lower right")

            #plot the optimal action percent as a function of slots
            axes[1][1].plot(optimal_percent,label="beta"+str(i))
            axes[1][1].set_xlabel("Slots")
            axes[1][1].set_ylabel("Percent")
            axes[1][1].set_title("Optimal action Selection")
            axes[1][1].legend(loc="lower right")
            axes[1][1].set_ylim([0, 1.0])

            #print the total regret accumulated over each experiment
            print("beta: The total regret accumulated over the experiment is :.4f.".format(str(i),total_regret))

            #print the average percentage of plays in which the optimal arm is pulled 
            print("beta: The average percentage of optimal arm is pulled is :.4f.".format(str(i),average_percent))

            i += 1
            reward = cumulative_reward[num_slot-1]
            R.append(reward)
            Percentage.append(average_percent)

    #Gradient bandit
    elif algo_name == Gradient:
        i = 1
        for para in para:

            #run the algorithm
            algo = algo_name(step_size = para[0], baseline = para[1], beta = para[2以上是关于Simulation | Multi-Armed Bandit Algorithm的主要内容，如果未能解决你的问题，请参考以下文章 
 关于Multi-Armed Bandit（MAB）问题及算法
 强化学习方法：探索-利用困境exploration exploitation，Multi-armed bandit
 强化学习专栏|多臂老虎机问题（Multi-armed Bandit Problem）
 solidworks的simulation的result没有了
 模拟：simulation，与 仿真：simulation
 模拟：simulation，与 仿真：simulation