第十三届蓝桥杯省赛 python B组复盘（三道代码题全AC居然省一了）

Posted 风信子的猫Redamancy

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了第十三届蓝桥杯省赛 python B组复盘（三道代码题全AC居然省一了）相关的知识，希望对你有一定的参考价值。

第十三届蓝桥杯省赛 python B组复盘（三道代码题全AC居然省一了）

🏆获奖感言

芜湖，努力是有结果的，这一个多月慢慢刷题，把数据结构和算法设计一步一步捡起来，也好好学习python的知识

终于一分耕耘一分收获咯，嘻嘻，开心，我居然拿了省一

其实考完以后，我个人感觉有点凉，因为感觉稍微的有点没什么信心，最后一道题没写几乎，倒数第二道题也胡乱写了一通，导致考完我就觉得随缘了，努努力就好了，没有抱太大希望，并且这之后，一点都不敢看这些试题了，给自己好好放松了

结果！！！我居然也有省一哈哈哈，我听到我朋友告诉我，我好开心哈哈，连忙分享给朋友们，也收到了恭喜，不错不错，嘻嘻，运气不错嘻嘻，而且排名也还是可以的，在前3%左右，看起来国奖还是有点希望的。

也有小伙伴跟我说，看了我讲解的视频，也拿了省一，都很不错，希望继续努力，在国赛也能拿个国奖回来。

好咯，开始复盘一下这次的蓝桥杯之路，顺便补补自己的短板，之后，也会出一期讲解视频嘻嘻

接下来所有的题目实际上都可以在C语言网进行提交，这里给出网址2022年第十三届蓝桥杯大赛软件类省赛Python大学B组真题

🌟 试题 A：排列字母

🤔 思路

这道题其实简单来说，就是一个排序问题，所以我几乎没怎么思考，直接调用sort函数，我后面还仔细看了看，害怕第一道题怎么那么简单哈哈，不过第一道题简单确实正常。

💻 代码

s = "WHERETHEREISAWILLTHEREISAWAY"
print(''.join(sorted(s))) # AAAEEEEEEHHHIIILLRRRSSTTWWWY

🌟 试题 B：寻找整数

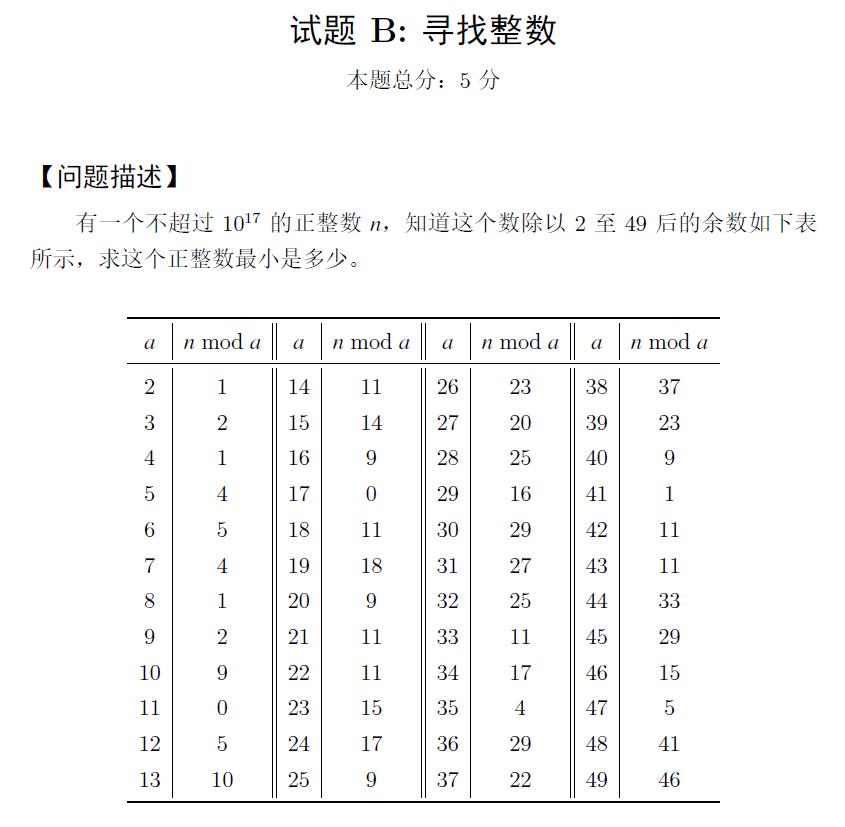
🤔 思路

这道题我现在想起来，依旧是心有余悸

当时我觉得最简单就是穷举嘛，反正硬生生穷举，并且考虑到python速度比较慢，我还用了C++来穷举，我想着四个小时起码出来吧，但是我大意了，即使后面我疯狂穷举，一天都还没出来，我无了，麻了。

听说正解是中国剩余定理，我在查资料的时候也看到一些有趣的解法，大家都还是蛮聪明的

有个朋友用暴力也搞了出来，真的人才，只能说这种枚举很聪明，但是感觉可遇不可求，他枚举到了一个等差数列，就是在满足一定条件下的数据是一个等差数列，接着就利用等差数列这个数据进行暴力穷举，30s得出最后答案，大家有兴趣也可以看一看2022第十三届蓝桥杯PythonB组

暴力三步走：

1.枚举数据找规律：取表后面5个大数判断更容易找到大数据，得到关键数据。

2.找出规律求公式：这些数字是按判断求得的，所以一定存在公式。

3.遍历公式找答案：通过公式进行快速遍历，30s轻松找到十六位数的答案。

💻 代码

#1.枚举数据找规律
i=1
while True:
    flag=True
    if i%49!=46:
        flag=False
    if i%48!=41:
        flag=False
    if i%47!=5:
        flag=False
    if i%46!=15:
        flag=False
    if i%45!=29:
        flag=False
    if flag:
        print(i)
    i+=1
'''
4772009
42909689
81047369
119185049
157322729
···
'''

#2.找出规律求公式
a=[4772009, 42909689, 81047369, 119185049,157322729]
#发现存在等差数列
print(a[1]-a[0])#38137680
print(a[2]-a[1])#38137680
print(a[3]-a[2])#38137680
k=38137680
b=4772009
#求出公式
y=k

#遍历公式
x=0
k=38137680
b=4772009
while True:
    flag=True
    y=k*x+b
    for i,j in mod:
        if y%i !=j:
            flag=False
            break
    if flag==True:
        print(y)#2022040920220409
        break
    x+=1

🌟 试题 C：纸张尺寸

题目描述

在 ISO 国际标准中定义了 A0 纸张的大小为 1189mm × 841mm，将 A0 纸沿长边对折后为 A1 纸，大小为 841mm × 594mm，在对折的过程中长度直接取下整（实际裁剪时可能有损耗）。将 A1 纸沿长边对折后为 A2 纸，依此类推。

输入纸张的名称，请输出纸张的大小。

输入

输入一行包含一个字符串表示纸张的名称，该名称一定是 A0、A1、A2、A3、A4、A5、A6、A7、A8、A9 之一。

输出

输出两行，每行包含一个整数，依次表示长边和短边的长度。

样例输入

A0

样例输出复制

1189
841

🤔 思路

这道题我觉得，相对于来说，还是比较简单的，因为其实题目已经固定了A0的纸张的大小，之后就是对A0的纸张不断的折叠。然后A后面的数字就是折叠的次数，比如A1是折叠一次，A2是折叠2次。。。

这之中注意两个点，第一，我们是对较长的边进行折叠

第二，就是我们首先输出长边，然后输出短边

💻 代码

s = input() 

t = int(s[-1]) # 最后一个数字也就是迭代的次数
w,h = 1189,841

for i in range(t):
    if w > h:
        w = w//2
    else:
        h = h//2
if w > h:
    print(w)
    print(h)
else:
    print(h)
    print(w)

大家的代码也可以去这里提交 🚀纸张尺寸

🌟 试题 D：数位排序

题目描述

小蓝对一个数的数位之和很感兴趣，今天他要按照数位之和给数排序。当两个数各个数位之和不同时，将数位和较小的排在前面，当数位之和相等时，将数值小的排在前面。

例如，2022 排在 409 前面，因为 2022 的数位之和是 6，小于 409 的数位之和 13。

又如，6 排在 2022 前面，因为它们的数位之和相同，而 6 小于 2022。

给定正整数 n，m，请问对 1 到 n 采用这种方法排序时，排在第 m 个的元素是多少？

输入

输入第一行包含一个正整数 n。

第二行包含一个正整数 m。

输出

输出一行包含一个整数，表示答案。

样例输入

13
5

样例输出

3

提示

1 到 13 的排序为：1, 10, 2, 11, 3, 12, 4, 13, 5, 6, 7, 8, 9。第 5 个数为 3。

对于 30% 的评测用例，1 ≤ m ≤ n ≤ 300。

对于 50% 的评测用例，1 ≤ m ≤ n ≤ 1000。

对于所有评测用例，1 ≤ m ≤ n ≤ 1 0 6 10^6 106。

🤔 思路

我觉得这其实就是一个排序问题，对于python来说，那我值需要设置一个排序规则即可，实际对于C++也有sort函数

所以思路就出来，首先创建我们需要的数组，然后定义一个排序规则，这个排序规则就是依照数位之和排序，所以定义了一个cmp函数计算数位之和，最后输出第m个数字就可以得到答案了

💻 代码

n = int(input())
l = [i for i in range(1,n+1)]
# 设置一个排序规则，计算数位之和
def cmp(x):
    ans = 0
    while x:
        ans += x%10
        x = x//10
    return ans 

l.sort(key = cmp)
m = int(input())
print(l[m-1])

大家的代码也可以去这里提交 🚀数位排序

🌟 试题 E：蜂巢

题目描述

蜂巢由大量的六边形拼接而成，定义蜂巢中的方向为：0 表示正西方向，1 表示西偏北 60◦，2 表示东偏北 60◦，3 表示正东，4 表示东偏南 60◦，5 表示西偏南 60◦。

对于给定的一点 O，我们以 O 为原点定义坐标系，如果一个点 A 由 O 点先向 d 方向走 p 步再向 (d + 2) mod 6 方向（d 的顺时针 120◦ 方向）走 q 步到达，则这个点的坐标定义为 (d, p, q)。在蜂窝中，一个点的坐标可能有多种。

下图给出了点 B(0, 5, 3) 和点 C(2, 3, 2) 的示意。

给定点 (d1, p1, q1) 和点 (d2, p2, q2)，请问他们之间最少走多少步可以到达？

输入

输入一行包含 6 个整数 d1, p1, q1, d2, p2, q2 表示两个点的坐标，相邻两个整数之间使用一个空格分隔。

输出

输出一行包含一个整数表示两点之间最少走多少步可以到达。

样例输入

0 5 3 2 3 2

样例输出

7

提示

对于 25% 的评测用例，p1, p2 ≤ 1 0 3 10^3 103 ；
对于 50% 的评测用例，p1, p2 ≤ 1 0 5 10^5 105 ；
对于 75% 的评测用例，p1, p2 ≤ 1 0 7 10^7 107 ；
对于所有评测用例，0 ≤ d1, d2 ≤ 5，0 ≤ q1 < p1 ≤ 1 0 9 10^9 109，0 ≤ q2 < p2 ≤ $10^9 $。

🤔 思路

这道题也真是搞脑子呀，当时看到这道题，想了好一会，想了很多种坐标系，结果几乎一个都没有对

在考完试和朋友讨论的时候，他跟我说，这道题可以用向量的想法，真是妙啊，那我们来看看

这样我们就可以将得到的坐标转化成0方向和1方向的向量，之后两个点的距离，就可以用我们的向量相减表示

不过之后，求最近距离的时候又分为两种情况，一种是符号相同的情况，符号相同的时候，也就是a+b或者-a-b这时候我们的距离就是|a+b|，也就是a+b的绝对值

但是对于符号不同的情况，我们就要取max(|a|,|b|)了，这里大概画图理解一下

💻 代码

d1,p1,q1,d2,p2,q2=map(int,input().split())

# 全部转化为0 方向 和 1方向的向量
def change(d,p,q):
    if d==0:return (p-q,q)
    if d==1:return (-q,p)
    if d==2:return (-p,p-q)
    if d==3:return (q-p,-q)
    if d==4:return (q,-p)
    if d==5:return (p,q-p)
s1=change(d1,p1,q1)
s2=change(d2,p2,q2)

# 向量的剑法
s=[s1[0]-s2[0],s1[1]-s2[1]]
a,b=s[0],s[1]
if a*b > 0: # ab同号
    print(abs(a+b))
else: # ab异号
  	print(max(abs(a),abs(b)))

大家的代码也可以去这里提交 🚀蜂巢

🌟 试题 F：消除游戏

题目描述

在一个字符串 S S S 中，如果 S i = S i − 1 S_i = S_i−1 Si​=Si−1​ 且 S i ≠ S i + 1 S_i \\ne S_i+1 Si​​=Si+1​，则称 S i S_i Si​ 和 S i + 1 S_i+1 Si+1​ 为边缘字符。如果且 S i ≠ S i − 1 S_i \\ne S_i-1 Si​​=Si−1​ ， S i = S i + 1 S_i = S_i+1 Si​=Si+1​，则 S i − 1 S_i−1 Si−1​ 和 S i S_i Si​ 也称为边缘字符。其它的字符都不是边缘字符。

对于一个给定的串 S，一次操作可以一次性删除该串中的所有边缘字符（操作后可能产生新的边缘字符）。

请问经过 2 64 2^64 264 次操作后，字符串 S 变成了怎样的字符串，如果结果为空则输出 EMPTY。

输入

输入一行包含一个字符串 S 。

输出

输出一行包含一个字符串表示答案，如果结果为空则输出 EMPTY。

样例输入

edda

样例输出

EMPTY

样例输入

sdfhhhhcvhhxcxnnnnshh

样例输出

s

提示

对于 25% 的评测用例，|S | ≤ 1 0 3 10^3 103 ，其中 |S | 表示 S 的长度；

对于 50% 的评测用例，|S | ≤ 1 0 4 10^4 104；

对于 75% 的评测用例，|S | ≤ 1 0 5 10^5 105 ；

对于所有评测用例，|S | ≤ 1 0 6 10^6 106，S 中仅含小写字母。

🤔 思路

其实这道题，我当时的想法很简单，就是暴力枚举嘛，简单暴力法

不断地进行判断，所以首先就定义一个函数，这个函数就是一个操作，然后再循环迭代2的64次方次，不过这里会涉及一个判断，如果发现，进行操作后，得到的字符串和上一次的字符串一样的时候，就说明不需要再次进行操作了，这时候就直接退出，得到我们的结果。

不过提交以后发现应该只能过75%的数据，不过能拿 3/4 的分也很不错了，这时候可以想想有什么好一点的算法

💻 代码

能过75%的数据

s = input()
def f(x):
    s = set()
    for i in range(1,len(x)-1):
        if (x[i] == x[i-1] and x[i] != x[i+1]):
            s.add(i)
            s.add(i+1)
        elif (x[i] != x[i-1] and x[i] == x[i+1]):
            s.add(i-1)
            s.add(i) 
    sr = ''
    for i in range(len(x)):
        if i not in s:
            sr += x[i]
    return sr
import copy
# 2的64次方操作
for i in range(1<<64):
    pre = copy.copy(s)
    s = f(s)
    if s == '':
        print('EMPTY')
        break
    elif pre == s:
        print(s)
        break

大家的代码也可以去这里提交 🚀消除游戏

🌟 试题 G：全排列的价值

题目描述

对于一个排列 A = (a1, a2, · · · , an)，定义价值 ci 为 a_1 至 a i − 1 a_i−1 ai−1​ 中小于 a i a_i ai​ 的数的个数，即 bi = | a j a_j aj​ | j < i, a j a_j aj​ < a i a_i 第十三届蓝桥杯省赛b组 两道dp补题

第十三届蓝桥杯省赛b组 两道dp补题

第十三届蓝桥杯省赛C++B组 真题题解（详细讲解+代码分析）看这篇就够了~~~

第十三届蓝桥杯省赛C++B组 真题题解（详细讲解+代码分析）看这篇就够了~~~

第十三届蓝桥杯省赛 JAVA B组（真题解析+个人体会）（已更新完G题）

十三届蓝桥杯省赛C++ B组