22022华东杯数学建模思路实时更新-ABC思路(AC完整程序)已更新-5月1日23时
Posted 小叶的趣味数模
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了22022华东杯数学建模思路实时更新-ABC思路(AC完整程序)已更新-5月1日23时相关的知识,希望对你有一定的参考价值。
【关注我,思路实时更新,详细思路持续更新。去年原创思路,被很多机构贩卖,都是免费的,程序也是免费的,以前是您好啊数模君/数模孵化园,现在改名啦,认准:小叶的趣味数模,原创发布,别被坑了】
目录
这是刚刚的华中思路及程序,供参考
A题【思路已更新,完整程序已更新】
目前普遍采用十合一混采样,可见相关政策文件
①
http://www.gov.cn/xinwen/2020-08/19/content_5535756.htm
②

一般来讲肯定是越多人混采效率越高,但是如果多人混检中发现了阳性,那么就反而会对增加工作量,那么本题的效率,我们可以看作是核酸检测次数,数据肯定很难找,内部资料应该很难拿到,不过也不是不可以做,这道题就从概率事件角度去描述问题,比如说设置一个区域内多少人口,阳性人数多少(可以参考新浪疫情、丁香园、百度疫情大数据),然后采用十合一,二十合一等,每个人给个编号,随机打乱组合,去模拟多次实验结果,如果混采发现阳性,那就需要重新对组内每个人都再采集一次,最后取平均核酸检测次数作为不同混采的结果,类似于优化问题,可以找到最优混采数量,第二问可以多研究结果地区,疫情网站上取某一天新增感染人数作为阳性人数,及当地总人口数,同第一问方法算一下,第三问会考虑多轮检测,结合实际来看,多轮采集就是为了避免开始检测无症状的感染病例,每轮检测后,真实的感染病例会减少,那么每轮混采肯定是人数会越来越多才对,那么第三问就模拟该情景进行分析说明。
第一问程序
clear
clc
person=1000;%地区人数
q=0.01;%阳性占比
%生成序列
P=[1:person,zeros(1,person)];%第一行为编号,第二行1为阳性
g=fix(person*q);
%将病例加入到序列中
a=randperm(person);
P(2,a(1:g))=1;
u=[5,30];%混采人数,自变量
x=[];
F=[];
m=0;
for i=u(1):u(2)
m=m+1;
x(m,1)=i;
%产生随机序列
f=[];
for j=1:100
p=P(:,randperm(person));
z=[];
n=0;
y=0;
while size(p,2)>=0
if fix(size(p,2)/x(m))>0
n=n+1;
zn,1=p(:,1:x(m));
if sum(zn,1(2,:))>0
y=y+x(m);
else
y=y+1;
end
p(:,1:x(m))=[];
elseif fix(size(p,2)/x(m))==0
break
else
n=n+1;
zn,1=p;
if sum(zn,1(2,:))>0
y=y+size(p,2);
else
y=y+1;
end
p=[];
end
end
f=[f;y];
end
F(m,1)=fix(mean(f));
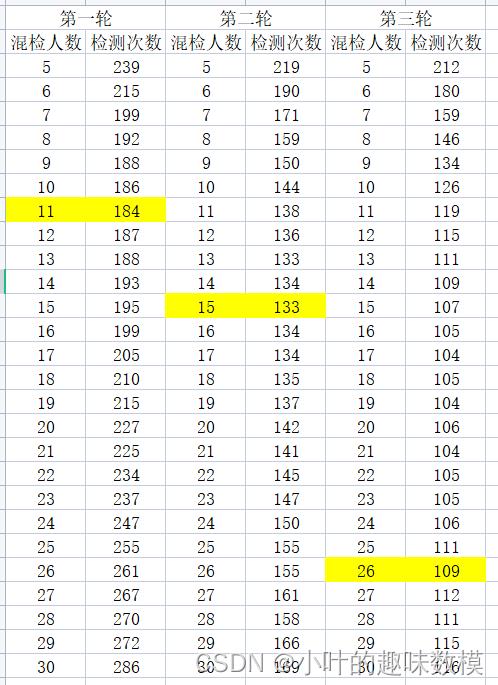
end第一问结果,参数自行设置,有的地方感染率小,那肯定是混采人数越大越好,有的地方感染率高,例如如下结果,混采11人时效率最高。


第二问就是带入地区的人口和新增感染人数去算,多个地区不同情况对比
第三问程序,参数可适当假设,最好是每轮核算后混检人数递增,这样才符合实际
clear
clc
person=1000;%地区人数
q=0.01;%阳性占比
r=0.5;%假设每轮筛出50%的阳性占比人数
%生成序列
P=[1:person,zeros(1,person)];%第一行为编号,第二行1为阳性
g=fix(person*q);
%将病例加入到序列中
a=randperm(person);
P(2,a(1:g))=1;
u=[5,30];%混采人数,自变量
xx=[];
FF=[];
for ii=1:3%假定进行三轮筛查
x=[];
F=[];
m=0;
for i=u(1):u(2)
m=m+1;
x(m,1)=i;
%产生随机序列
f=[];
for j=1:100
p=P(:,randperm(person));
z=[];
n=0;
y=0;
while size(p,2)>=0
if fix(size(p,2)/x(m))>0
n=n+1;
zn,1=p(:,1:x(m));
if sum(zn,1(2,:))>0
y=y+x(m);
else
y=y+1;
end
p(:,1:x(m))=[];
elseif fix(size(p,2)/x(m))==0
break
else
n=n+1;
zn,1=p;
if sum(zn,1(2,:))>0
y=y+size(p,2);
else
y=y+1;
end
p=[];
end
end
f=[f;y];
end
F(m,1)=fix(mean(f));
end
%每轮核酸会剔除一部分感染者
b=find(P(2,:)==1);
if length(b)>0
c=randperm(length(b));
if fix(length(c)*r)>0
P(:,b(c(1:fix(length(c)*r))))=[];
end
end
%记录每轮结果
xxii,1=x;
FFii,1=F;
end第三问结果,假定三轮核酸,结果数据在xx和FF矩阵汇总,以下结果我们可以看出,第一轮核酸可采用11人混检,第二轮15人混检,第三轮26人混检,效率最高。
B题
刚好华中B题也是股票投资问题,可以去看下我写的思路

其实基本上就是这道题的大概思路了
C题
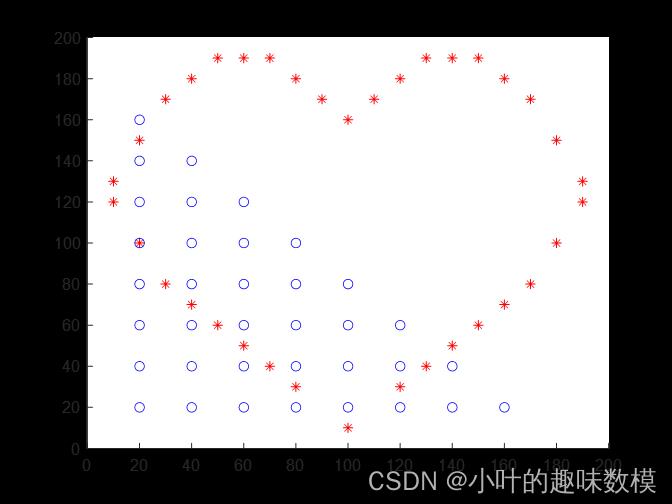
本题可用优化算法求解,第一问不考虑转向的时间成本,那么就直接寻找最短路即可,一组变量是小车的初始位置,另一组变量是目的地编号,随机赋予小车目的地编号,速度为10cm/s,以最后一辆小车到达目的地的时间作为目标函数进行寻优,可以采用遗传算法和模拟退火算法
第一问结果
第一问完整程序如下
clear
clc
%1cm为一个刻度,这是小车初始的均匀分布
XX=[20,160;20,140;20,120;20,100;20,80;20,60;20,40;20,20;
40,140;40,120;40,100;40,80;40,60;40,40;40,20;60,120;
60,100;60,80;60,60;60,40;60,20;80,100;80,80;80,60;80,40;
80,20;100,80;100,60;100,40;100,20;120,60;120,40;120,20;
140,40;140,20;160,20];
n=length(XX);
%目标分布点,可自己设置分布点,这里是个案例
YY=[100,10;120,30;130,40;140,50;150,60;160,70;170,80;180,100;
190,120;190,130;180,150;170,170;160,180;150,190;140,190;
130,190;120,180;110,170;100,160;80,30;70,40;60,50;50,60;
40,70;30,80;20,100;10,120;10,130;20,150;30,170;40,180;
50,190;60,190;70,190;80,180;90,170];
figure
hold on
plot(YY(:,1),YY(:,2),'r*')
plot(XX(:,1),XX(:,2),'bo')
title('初始分布位置')
num=10;%种群大小
num_gen=10;%最大迭代次数
q1=0.7;%交叉率
q2=0.7;%变异率
chrom=[];
f=[];
for i=1:num
chrom(i,:)=randperm(n);
f(i,1)=fun(chrom(i,:),XX,YY,n);%目标函数,总时间
end
[bestf,b]=min(f);
bestchrom=chrom(b,:);
trace(1)=min(f);
for k_gen=1:num_gen
selchrom=chrom;%选择,寻优维度较高,这里就全部进行交叉遗传
selchrom=jiaocha(selchrom,q1,k_gen,num_gen);
selchrom=bianyi(selchrom,q2,k_gen,num_gen);
ff=[];
for i=1:num
ff(i,1)=fun(selchrom(i,:),XX,YY,n);%目标函数,总时间
end
%两代合并排序
f=[f;ff];
chrom=[chrom;selchrom];
[f,b]=sort(f);
chrom=chrom(b,:);
f=f(1:num,:);
chrom=chrom(1:num,:);
trace=[trace;min(f)];
end
%迭代图
figure
plot(trace)
xlabel('迭代次数')
ylabel('总时间/s');
%最优结果
[bestf,b]=min(f);
bestchrom=chrom(b,:);
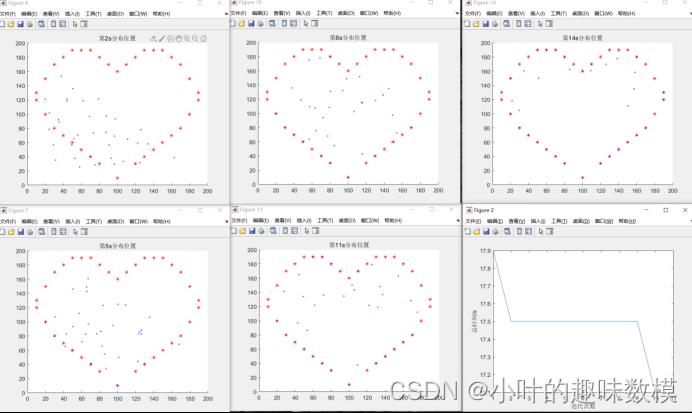
[~,T]=fun(bestchrom,XX,YY,n);%每0.1s位置分布情况
for i=1:length(T)
if mod(i,10)==0
figure
hold on
plot(YY(:,1),YY(:,2),'r*')
plot(Ti,1(:,1),Ti,1(:,2),'bo','MarkerSize',2)
title(["第"+num2str(i/10)+"s分布位置"])
end
endfunction [f,T]=fun(x,XX,YY,n)
chrom=x;
f=[];
X=XX;
Y=YY;
t=1;%开始时刻
T=[];
Tt,1=X;%记录每时刻小车位置
%且小车在运动过程中严禁碰撞,以0.1s为单位时间进行模拟
%每次更新位置,如果有存在碰撞时,则考虑等待下一个0.1s再移动
%每0.1s按速度来算就移动1cm
v=1;
%半径
r=1;
d=sum(sum(abs(X-Y(chrom,:))));%判断是否所有小车到达目的地
while d>0
for j=1:n
%如果目标点离小车超过0.1s的行程
if pdist2(X(j,:),Y(chrom(j),:))>v
%如果目标点和小车不在竖直方向上
if Y(chrom(j),1)~=X(j,1)
%如果目标点在小车左边
if Y(chrom(j),1)>X(j,1)
k=(Y(chrom(j),2)-X(j,2))/(Y(chrom(j),1)-X(j,1));
theta=atan(k);
X(j,1)=X(j,1)+cos(theta)*v;
X(j,2)=X(j,2)+sin(theta)*v;
%如果目标点在小车右边
elseif Y(chrom(j),1)<X(j,1)
k=(Y(chrom(j),2)-X(j,2))/(Y(chrom(j),1)-X(j,1));
theta=atan(k);
X(j,1)=X(j,1)-cos(theta)*v;
X(j,2)=X(j,2)-sin(theta)*v;
end
%如果目标点和小车在竖直方向上
else
X(j,1)=X(j,1);
%如果目标点y坐标>小车y坐标
if Y(chrom(j),2)>X(j,2)
X(j,2)=X(j,2)+v;
%如果目标点y坐标<小车y坐标
elseif Y(chrom(j),2)<X(j,2)
X(j,2)=X(j,2)-v;
end
end
%如果目标点离小车不到0.1s的行程
else
X(j,1)=Y(chrom(j),1);
X(j,2)=Y(chrom(j),2);
end
end
%判断是否发生碰撞
%有的话就等候
%可能会有多辆车碰撞,因此这里采用DBSCAN聚类
D1=pdist2(X,X);
[D1,D2]=sort(D1,2);
a=find(D1(:,2)<r);
if length(a)>0
epsilon=r*2; %最大间距 需要参考点之间的距离设置合适的间距
MinPts=1; %半径内最少满足纳入集群的个数
IDX3=DBSCAN(X,epsilon,MinPts);
b=tabulate(IDX3);
c=find(b(:,2)>1);
g=[];
for k=1:length(c)
e=find(IDX3==c(k));
h=[];
for L=1:length(e)
if pdist2(X(e(L),:),Y(chrom(e(L)),:))<v
h=[h,L];
end
end
e(h)=[];
if length(e)>1
g=[g;e(2:end)];
end
end
if length(g)>0
X(g,:)=Tt,1(g,:);
end
end
t=t+1;
Tt,1=X;
d=sum(sum(abs(X-Y(chrom,:))));
end
%计算目标函数
f=(length(T)-1)/10;%记录最后小车到达目的地的时间
endfunction x=jiaocha(x,a,k_gen,num_gen)
%交叉率变化
a = a*exp(-k_gen/num_gen);
for i = 1:size(x,1)
if rand < a
%选择交叉位点
b = randi(size(x,2))-1;
x(i,:)=[x(i,b+1:end),x(i,1:b)];
end
endfunction x=bianyi(x,a,k_gen,num_gen)
%变异率变化
a = a*exp(-k_gen/num_gen);
for i = 1:size(x,1)
if rand < a
%选择变异位点
b1 = randi(size(x,2));
b2 = randi(size(x,2));
%产生变异(针对序列问题,产生两个变异点进行两两交换)
c = x(i,b1);
x(i,b1)=x(i,b2);
x(i,b2)=c;
end
endfunction [IDX, isnoise]=DBSCAN(X,epsilon,MinPts)
%首先定义个函数ExpandCluster
function ExpandCluster(i,Neighbors,C)
IDX(i)=C;
k = 1;
while true
j = Neighbors(k);
if ~visited(j)
visited(j)=true;
Neighbors2=find(D(j,:)<=epsilon);
if numel(Neighbors2)>=MinPts
%numel函数用于计算数组中满足指定条件的元素个数
Neighbors=[Neighbors Neighbors2];
end
end
if IDX(j)==0
IDX(j)=C;
end
k = k + 1;
if k > numel(Neighbors)
%numel函数用于计算数组中满足指定条件的元素个数
break;
end
end
end
C=0; %初始化参数
n=size(X,1);
IDX=zeros(n,1);
D=pdist2(X,X); %计算各个点之间的距离
visited=false(n,1); %false:创建逻辑矩阵(0和1,0表示真,1表示假)
isnoise=false(n,1);
%% 下面这段程序是每次循环先生成各个小集群,然后在以这些小集群为基础逐步扩大范围
for i=1:n
if ~visited(i)
visited(i)=true; %true相当于0,表示事件正确
%先定初始集群
Neighbors=find(D(i,:)<=epsilon);
if numel(Neighbors)<MinPts
%numel函数用于计算数组中满足指定条件的元素个数
isnoise(i)=true;
else
C=C+1;
%扩大集群
ExpandCluster(i,Neighbors,C);
end
end
end
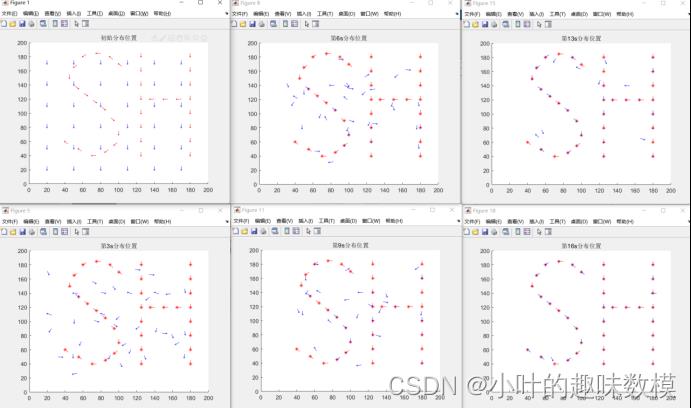
end第二问考虑转向在第一问模型上进行改进
第二问结果

完整程序如下(自定义函数与第一问共用)
clear
clc
%1cm为一个刻度,这是小车初始的均匀分布,第三列是角度
XX=[20,20,90;50,20,90;80,20,90;110,20,90;140,20,90;170,20,90;
20,50,90;50,50,90;80,50,90;110,50,90;140,50,90;170,50,90;
20,80,90;50,80,90;80,80,90;110,80,90;140,80,90;170,80,90;
20,110,90;50,110,90;80,110,90;110,110,90;140,110,90;170,110,90;
20,140,90;50,140,90;80,140,90;110,140,90;140,140,90;170,140,90;
20,170,90;50,170,90;80,170,90;110,170,90;140,170,90;170,170,90];
XX(:,3)=XX(:,3)./360.*2.*pi;
n=length(XX);
%目标分布点,可自己设置分布点,这里是个案例,第三列是角度
YY=[40,60,-45;55,50,-45;70,40,0;85,45,45;95,55,45;100,70,90;
95,90,135;85,105,135;75,115,135;65,125,135;55,135,135;45,150,90;
50,165,45;60,180,45;75,185,0;90,180,-45;100,170,-45;125,180,90;
125,160,90;125,140,90;125,120,90;125,100,90;125,80,90;125,60,90;
125,40,90;135,120,0;150,120,0;165,120,0;180,180,90;180,160,90;
180,140,90;180,120,90;180,100,90;180,80,90;180,60,90;180,40,90];
YY(:,3)=YY(:,3)./360.*2.*pi;
figure
hold on
plot(YY(:,1),YY(:,2),'r*','MarkerSize',2)
plot(XX(:,1),XX(:,2),'bo','MarkerSize',2)
for i=1:size(XX,1)
plot([YY(i,1),YY(i,1)+5*cos(YY(i,3))],[YY(i,2),YY(i,2)+5*sin(YY(i,3))],'r-')
plot([XX(i,1),XX(i,1)+5*cos(XX(i,3))],[XX(i,2),XX(i,2)+5*sin(XX(i,3))],'b-')
end
axis([0,200,0,200])
title('初始分布位置')
num=10;%种群大小
num_gen=10;%最大迭代次数
q1=0.7;%交叉率
q2=0.7;%变异率
chrom=[];
f=[];
for i=1:num
chrom(i,:)=randperm(n);
f(i,1)=fun2(chrom(i,:),XX,YY,n);%目标函数,总时间
end
[bestf,b]=min(f);
bestchrom=chrom(b,:);
trace(1)=min(f);
for k_gen=1:num_gen
selchrom=chrom;%选择,寻优维度较高,这里就全部进行交叉遗传
selchrom=jiaocha(selchrom,q1,k_gen,num_gen);
selchrom=bianyi(selchrom,q2,k_gen,num_gen);
ff=[];
for i=1:num
ff(i,1)=fun2(selchrom(i,:),XX,YY,n);%目标函数,总时间
end
%两代合并排序
f=[f;ff];
chrom=[chrom;selchrom];
[f,b]=sort(f);
chrom=chrom(b,:);
f=f(1:num,:);
chrom=chrom(1:num,:);
trace=[trace;min(f)];
end
%迭代图
figure
plot(trace)
xlabel('迭代次数')
ylabel('总时间/s');
%最优结果
[bestf,b]=min(f);
bestchrom=chrom(b,:);
[~,TTT]=fun2(bestchrom,XX,YY,n);%每0.1s位置分布情况
for i=1:length(TTT)
if mod(i,10)==0
figure
hold on
plot(YY(:,1),YY(:,2),'r*')
plot(TTTi,1(:,1),TTTi,1(:,2),'bo','MarkerSize',2)
for j=1:size(XX,1)
plot([YY(j,1),YY(j,1)+5*cos(YY(j,3))],[YY(j,2),YY(j,2)+5*sin(YY(j,3))],'r-')
plot([TTTi,1(j,1),TTTi,1(j,1)+5*cos(TTTi,1(j,3))],[TTTi,1(j,2),TTTi,1(j,2)+5*sin(TTTi,1(j,3))],'b-')
end
axis([0,200,0,200])
title(["第"+num2str(i/10)+"s分布位置"])
end
endfunction [f,TTT]=fun2(x,XX,YY,n)
chrom=x;
f=[];
X=XX;
Y=YY;
%每0.1s按速度来算就移动1cm
v=1;
%半径
r=5;
%转弯半径
R=15;
T=[];
for i=1:n
t=[];
z1=X(i,:);
z2=Y(chrom(i),:);
t=[t;z1];
d=pdist2(z1(1:2),z2(1:2));%判断是否所有小车到达目的地
%当小车与目的方向相同时
if z1(3)==z2(3)
while d>0
k=(z2(2)-z1(2))/(z2(1)-z1(1));
if z2(1)>z1(1)
theta=atan(k);
elseif z2(1)<z1(1) & z2(2)>z1(2)
theta=pi-atan(-k);
elseif z2(1)<z1(1) & z2(2)<z1(2)
theta=atan(k)-pi;
end
if z2(2)<z1(2)
theta1=theta+pi;
else
theta1=theta;
end
if d>v
z1=[z1(1)+cos(theta)*v,z1(2)+sin(theta)*v,theta1];
d=pdist2(z1(1:2),z2(1:2));
t=[t;z1];
else
z1=z2;
d=pdist2(z1(1:2),z2(1:2));
t=[t;z1];
end
end
end
%当目的方向cos为正时
if cos(z2(3))>0
flag=0;
o=[z1(1)+R,z1(2)];%圆心
while d>0
while flag==0
zz1=[o(1)+R*cos(pi-v/R),o(2)+R*sin(pi-v/R),z1(3)-v/R];
if z2(3)<z1(3) & z2(3)<zz1(3)
z1=zz1;
d=pdist2(z1(1:2),z2(1:2));
t=[t;z1];
else
z1=[zz1(1:2),z2(3)];
d=pdist2(z1(1:2),z2(1:2));
t=[t;z1];
flag=1;
end
end
if flag==1
k=(z2(2)-z1(2))/(z2(1)-z1(1));
if z2(1)>z1(1)
theta=atan(k);
elseif z2(1)<z1(1) & z2(2)>z1(2)
theta=pi-atan(-k);
elseif z2(1)<z1(1) & z2(2)<z1(2)
theta=atan(k)-pi;
end
if z2(2)<z1(2)
theta1=theta+pi;
else
theta1=theta;
end
if z2(2)>0 & z2(3)>=0
theta1=theta1;
elseif z2(2)>0 & z2(3)<0
theta1=-theta1;
end
if d>v
z1=[z1(1)+cos(theta)*v,z1(2)+sin(theta)*v,theta1];
d=pdist2(z1(1:2),z2(1:2));
t=[t;z1];
else
z1=z2;
d=pdist2(z1(1:2),z2(1:2));
t=[t;z1];
end
end
end
end
%当目的方向cos为负时
if cos(z2(3))<0
flag=0;
o=[z1(1)-R,z1(2)];%圆心
while d>0
while flag==0
zz1=[o(1)+R*cos(v/R),o(2)+R*sin(v/R),z1(3)+v/R];
if z2(3)>z1(3) & z2(3)>zz1(3)
z1=zz1;
d=pdist2(z1(1:2),z2(1:2));
t=[t;z1];
else
z1=[zz1(1:2),z2(3)];
d=pdist2(z1(1:2),z2(1:2));
t=[t;z1];
flag=1;
end
end
if flag==1
k=(z2(2)-z1(2))/(z2(1)-z1(1));
if z2(1)>z1(1)
theta=atan(k);
elseif z2(1)<z1(1) & z2(2)>z1(2)
theta=pi-atan(-k);
elseif z2(1)<z1(1) & z2(2)<z1(2)
theta=atan(k)-pi;
end
if z2(2)<z1(2)
theta1=theta+pi;
else
theta1=theta;
end
if z2(2)>0 & z2(3)>=0
theta1=theta1;
elseif z2(2)>0 & z2(3)<0
theta1=-theta1;
end
if d>v
z1=[z1(1)+cos(theta)*v,z1(2)+sin(theta)*v,theta1];
d=pdist2(z1(1:2),z2(1:2));
t=[t;z1];
else
z1=z2;
d=pdist2(z1(1:2),z2(1:2));
t=[t;z1];
end
end
end
end
Ti,1=t;
end
tt=[];
TT=[];
for i=1:size(T,1)
TT=[TT;Ti,1(1,:)];
Ti,1(1,:)=[];
tt(i,1)=length(Ti,1);
end
TTT1,1=TT;
u=1;
while sum(tt)>0
TT=[];
for i=1:size(T,1)
if tt(i,1)>0
TT=[TT;Ti,1(1,:)];
Ti,1(1,:)=[];
tt(i,1)=length(Ti,1);
else
TT=[TT;TTTu,1(i,:)];
end
end
%判断是否发生碰撞
%有的话就等候
%可能会有多辆车碰撞,因此这里采用DBSCAN聚类
D1=pdist2(TT(:,1:2),TT(:,1:2));
[D1,D2]=sort(D1,2);
a=find(D1(:,2)<r);
if length(a)>0
epsilon=r*2; %最大间距 需要参考点之间的距离设置合适的间距
MinPts=1; %半径内最少满足纳入集群的个数
IDX3=DBSCAN(TT(:,1:2),epsilon,MinPts);
b=tabulate(IDX3);
c=find(b(:,2)>1);
g=[];
for k=1:length(c)
e=find(IDX3==c(k));
h=[];
for L=1:length(e)
if pdist2(TT(e(L),1:2),Y(chrom(e(L)),1:2))<v
h=[h,L];
end
end
e(h)=[];
if length(e)>1
g=[g;e(2:end)];
end
end
if length(g)>0
TT(g,:)=TTTu,1(g,:);
end
end
u=u+1;
TTTu,1=TT;
end
f=(length(TTT)-1)/10;%记录最后小车到达目的地的时间
end以上是关于22022华东杯数学建模思路实时更新-ABC思路(AC完整程序)已更新-5月1日23时的主要内容,如果未能解决你的问题,请参考以下文章
 https://blog.csdn.net/qq_39899679/article/details/124502977
https://blog.csdn.net/qq_39899679/article/details/124502977