2022五一数学建模思路实时更新-ABC思路已更新-5月2日0时

Posted 2022-05-02 小叶的趣味数模

【关注我，思路实时更新，详细思路持续更新。去年原创思路，被很多机构贩卖，都是免费的，程序也是免费的，以前是您好啊数模君/数模孵化园，现在改名啦，认准：小叶的趣味数模，原创发布，别被坑了】

目录

A题

B题

C题

---

A题

规划问题-优化算法求解

血管机器人这几个条件需要注意：

①血管机器人在患者血管中工作时间是一周，一周后必须取出；

②血管机器人取出后，操作手拆卸下来，需要进行一周的保养才能再次开展工作

③操作手如没有安排工作，则一直需要保养

④新购买的容器艇需要经过一周的检查调试后才可以投入使用

⑤容器艇使用后并不必须要保养，可以连续使用

⑥容器艇如果未使用过需要保养

⑦一个容器艇配四个熟练操作手

⑧操作手学习时不需要容器艇参与

※该医院从第1周开始开展血管机器人治疗业务，并假定开始前已经有了13个容器艇和50个熟练操作手，可直接使用

这道题一定要读懂题目，别盲目下笔，附件2有说每周使用的数量

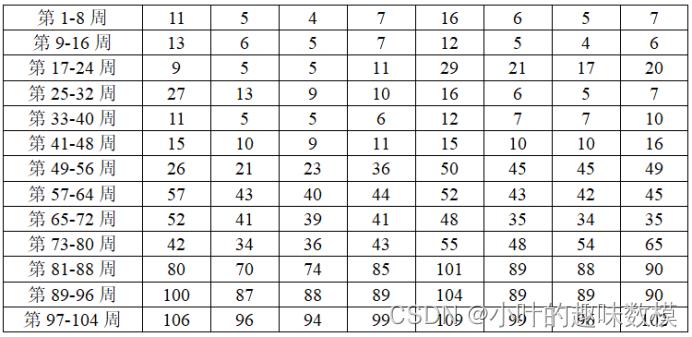
第一问，目前医院有可以直接使用的13个容器艇和50个熟练操作手，第一周就会用到11个容器艇和44个操作手，那么留下来能训练新操作手的就只有6个，那么最多能训练60个，再看第二周患者5人，需要容器艇5个和20个操作手，原本有六个，与此同时还要考虑第三周的需求（因为第二周需要空余操作手来训练第三周需要用到的操作手），第三周会用到4个机器人，第二周购买后怎么也可以满足第三周需求，那么为了满足第二周第三周的需求，第一周就至少需要购买14个且至多购买60个操作手，这道题就是特别要注意每周需要购买的容器艇和操作手数量范围需要根据附件2需求进行推算，没有需求就是0，第一问8周就需要确定8*2个变量（分别是容器艇数量和操作手数量）范围，有了自变量范围，接下来就是以成本最下话寻优。

第二问考虑损毁，那么在第一问基础上，还是同样的，损毁就会增加需求和成本，首先还是简确定每周容器艇和操作手的购买数量范围，然后进行寻优

第三问，指导数量增加，但每周有10%的机器人损毁，同样的在第一问基础上加条件，然后寻优

第四问主要涉及到成本问题，在第一问基础上增加成本目标函数，进行多目标寻优，推荐采用NS2排序算法求得最优解集

第五问，这里的预测就直接时间序列就好了，在第四问的基础上增加条件进行寻优。

B题

本题主要是神经网络、机器学习预测

这几个条件需要注意

①假设矿石加工过程需要经过系统I和系统II两个环节，两个环节不分先后，其他条件（电压、水压等）保持不变。

②生产技术人员可以通过传入调温指令，调节温度来改变产品质量。其中系统I和II的温度数据见附件1和附件2。

③矿石加工过程为2小时整（即：在调节温度2个小时后，可检测得到该调节温度所对应的矿石产品质量的评价指标（A,B,C,D））

④假设每次温度调节之后的2个小时内不会传入新的调温指令，调温指令下达后系统温度基本与调温指令设定的温度相同，但是有轻微波动

第一问，需要根据构建出系统温度和原矿参数预测产品质量的方法，时间肯定是要以产品质量数据的时间为准，质量评价指标ABCD是调节温度两小时后得到的（两小时内温度有轻微波动），附件中的质量数据是一小时得出一个结果，所以说温度数据需要依次取2小时片段数据取平均值来对应质量指标数据，原矿参数是哪一天的这一天的数据训练都用这天的值就行了

数据处理好后就代入模型训练，可能性最大的产品指标其实就是模型训练后你预测的结果，模型训练好后，带入表1中两组系统温度和对应23号的原矿参数，输出以下四个指标ABCD

后面问不管正向预测还是反向预测，都基本是同样的模型，注意做模型的误差检验，这道题推荐所有队伍选择，机器学习算法现学也很快

第二问就是反过来训练，去预测温度，同样的模型套用即可

第三问，先根据表3和附件2的ABCD三个指标给数据贴上合格和不合格的标签，进行二分类训练，然后带入数据去预测

第四问，前面训练的模型可以当做目标函数，自变量为系统温度1、2，套一个优化算法进行寻优

C题

本题主要用到excel

这几个条件需要注意

①探测器的灵敏度决定了对火灾特征响应的灵敏程度，但较高的灵敏度会导致报警可靠性的降低，而较高的可靠性则需要牺牲探测器的灵敏度

②当某一建筑内多个火灾探测器的机号与回路编号相同时且这些探测器均发出火灾报警信号，则认为是同一起火灾事故

③地址编码是建筑，用户编码可以看成其中的房间或者区域

第一问，首先根据附件1确定该城市6月1日至6月18日的真实火灾起数，做法就是做字符计数，excel都能实现，然后对每个建筑内各个探测器的故障频数统计，得到故障率，然后排序做评价。

选择合适参数建立区域报警部件类型智能研判模型，这里的合适参数其实就是指回路数，也就表示不同探测器的灵敏度，其实后面问应当考虑每种探测器（部件名称）的最佳回路数，那么肯定就需要先得到不同探测器的回路数与故障率的关系式。

第三问就是评价，除了题目说到的辖区火灾发生频率、部件故障率、部件可靠性等指标，自己还可以增加一些。