支持向量机SVM原理解读，以及PyQt5融合SVM的代码实现，没有公式推导（已经很成熟，很难改公式，数学专业的可以推导学习）
Posted Flying Bulldog
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了支持向量机SVM原理解读，以及PyQt5融合SVM的代码实现，没有公式推导（已经很成熟，很难改公式，数学专业的可以推导学习）相关的知识，希望对你有一定的参考价值。
如标题所言，本文没有公式推导，感兴趣的可以了解，公式推导链接直达：
机器学习 | 深入SVM原理及模型推导（一） - 知乎 (zhihu.com)
https://zhuanlan.zhihu.com/p/199224848深入理解SVM系列（二）软间隔与对偶问题 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/213778201详解SVM模型——核函数是怎么回事 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/261061617
目录
（1）效果展示：
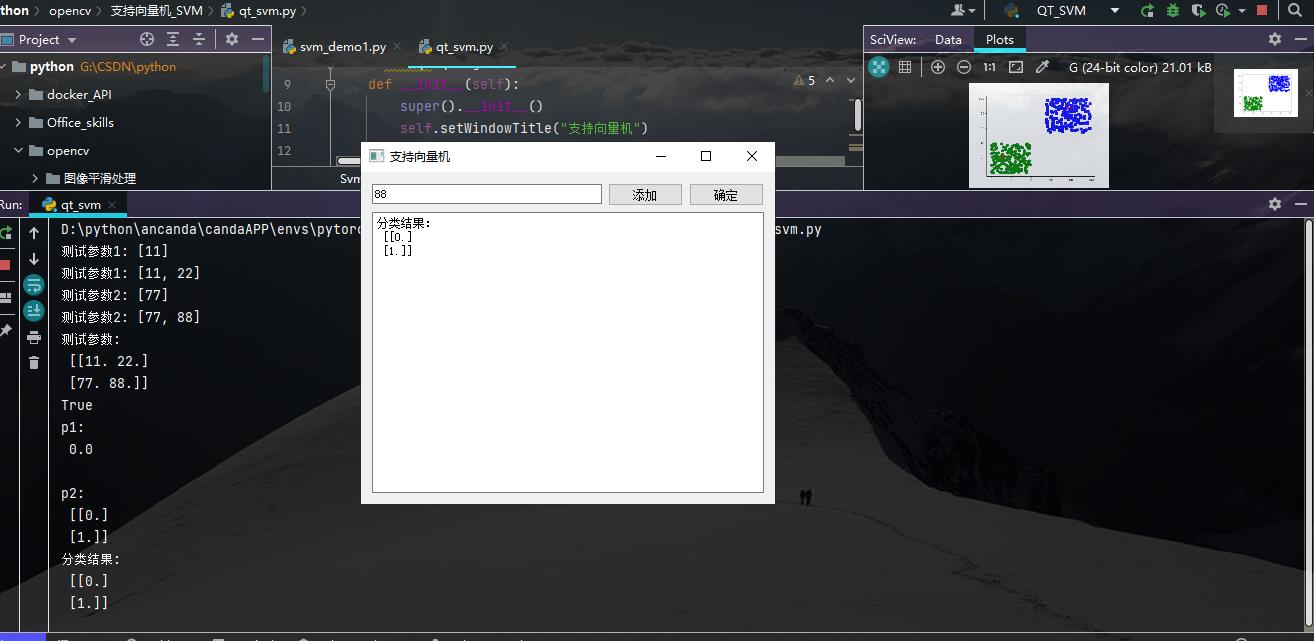
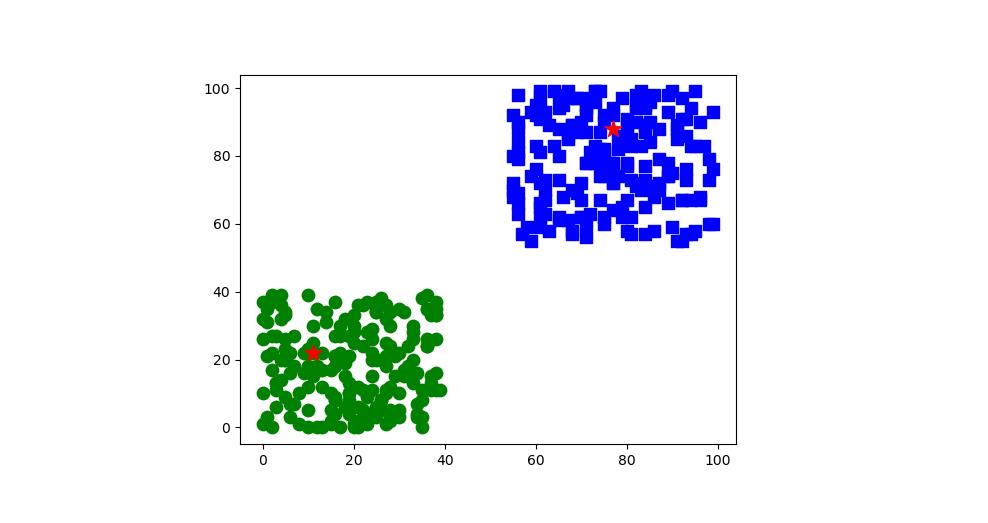
（2）PyQt5的代码示例：
import numpy as np
from PyQt5.QtWidgets import QWidget, QPushButton, QApplication, QLineEdit, QTextEdit, \\
QVBoxLayout, QHBoxLayout
import sys
from svm_demo1 import main
class Svm_Qt(QWidget):
"""
此处传参数有些许局限，可以自行改进
操作方法：每一次输入（0， 100）的数字，点击添加，重复4次，最后点击确定，即可得出分类结果
"""
def __init__(self):
super().__init__()
self.setWindowTitle("支持向量机")
self.setGeometry(60, 60, 400, 300)
# # 定义控件
self.le = QLineEdit(self) # 单行文本框
# self.le.move(50, 50)
self.ptn0 = QPushButton('添加', self) # 按钮
self.ptn1 = QPushButton('确定', self) # 按钮
self.te = QTextEdit(self) # 多行文本框
# # 布局
layout1 = QHBoxLayout() # 水平布局
layout1.addWidget(self.le)
layout1.addWidget(self.ptn0)
layout1.addWidget(self.ptn1)
layout2 = QVBoxLayout() # 垂直布局
layout2.addLayout(layout1)
layout2.addWidget(self.te)
self.setLayout(layout2)
# # 定义槽（控件连接自定义函数）
self.ptn0.clicked.connect(self.tj)
self.ptn1.clicked.connect(self.show_QTextEdit)
self.le.textChanged.connect(self.judge)
# # 存放待测参数
self.texts = []
self.texts_1 = []
def judge(self, text):
self.text = int(text)
def tj(self):
if len(self.texts) != 2:
self.texts.append(self.text)
print("测试参数1:", self.texts)
else:
self.texts_1.append(self.text)
print("测试参数2:", self.texts_1)
if len(self.texts_1) == 2:
self.test = np.array((self.texts, self.texts_1), dtype='float32')
print("测试参数:", "\\n", self.test)
def show_QTextEdit(self, s):
if s is False:
self.result = main(self.test) # self.test = [a, b], [c, d]
print("分类结果:", "\\n", self.result)
self.te.setPlainText("分类结果：\\n %s" % str(self.result))
if __name__ == '__main__':
app = QApplication(sys.argv) # 初始化界面
svm_qt = Svm_Qt() # 类实例化
svm_qt.show() # 展示界面
sys.exit(app.exec_()) # 无线循环界面
（3）SVM原理解读：
支持向量机（Support Vector Machine，SVM）是一种二分类模型，目标是寻找一个标准（称为超平面）对样本数据进行分割，分割的原则是确保分类最优化（类别之间的间隔最大）。
Python 提供了不同的实现支持向量机的库（例如 sk-learn 库、LIBSVM 库等），OpenCV 也 提供了对支持向量机的支持，对于上述库，基本都可以直接使用，本文介绍opencv的方法。
- 用于划分不同类别的直线，就是分类器。在构造分类器时，非常重要的一项 工作就是找到最优分类器。
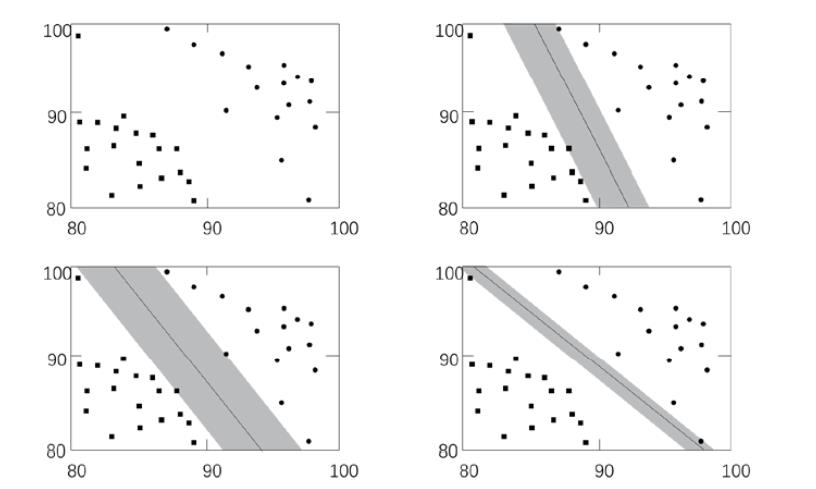
- 离分类器最近的点到分类器的距离称为间隔（margin）。我们希望间隔尽可能地大， 这样分类器在处理数据时，就会更准确。
- 离分类器最近的那些点叫作支持向量（support vector）。正是这些支持向量，决定了分类器 所在的位置。
- 具体图片如下所示：
支持向量机在处理数据时，如果在低维空间内无法完成分类，就会自动将数据映射到高维空间，使其变为（线性）可分的。简单地讲，就是对当前数据进行函数映射操作。
如下图所示，在分类时，通过函数 f 的映射，让左图中本来不能用线性分类器分类的数据变为右图中线性可分的数据。当然，在实际操作中，也可能将数据由低维空间向高维空间转换。
数据由低维空间转换到高维空间后运算量会呈几何级增加，但实际上， 支持向量机能够通过核函数有效地降低计算复杂度。
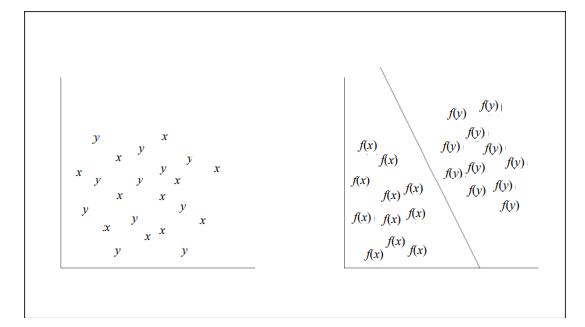
原理总结：
1. 尽管上面分析的是二维数据，但实际上支持向量机可以处理任何维度的数据。在不同的维 度下，支持向量机都会尽可能寻找类似于二维空间中的直线的线性分类器。例如，在二维空间， 支持向量机会寻找一条能够划分当前数据的直线；在三维空间，支持向量机会寻找一个能够划 分当前数据的平面（plane）；在更高维的空间，支持向量机会尝试寻找一个能够划分当前数据的超平面（hyperplane）。
2. 一般情况下，把能够可以被一条直线（更一般的情况，即一个超平面）分割的数据称为线 性可分的数据，所以超平面是线性分类器。
3. “支持向量机”是由“支持向量”和“机器”构成的。
- “支持向量”是离分类器最近的那些点，这些点位于最大“间隔”上。通常情况下，分类仅依靠这些点完成，而与其他点无关。
- “机器”指的是分类器。
综上所述，支持向量机是一种基于关键点的分类算法。
（4）opencv中的SVM三步走
********三步：创建空分类器、训练、预测********
1. 在使用支持向量机模块时，需要先使用函数 cv2.ml.SVM_create()生成用于后续训练的空分类器模型。该函数的语法格式为：
svm = cv2.ml.SVM_create( )
2. 获取了空分类器 svm 后，针对该模型使用 svm.train()函数对训练数据进行训练，其语法格 式为：
训练结果= svm.train(训练数据,训练数据排列格式,训练数据的标签)
- 训练数据排列格式：原始数据的排列形式有按行排列（cv2.ml.ROW_SAMPLE，每一条 训练数据占一行）和按列排列（cv2.ml.COL_SAMPLE，每一条训练数据占一列）两种形式，根据数据的实际排列情况选择对应的参数即可。
3. 完成对分类器的训练后，使用 svm.predict()函数即可使用训练好的分类器模型对测试数据进行分类，其语法格式为：
(返回值,返回结果) = svm.predict(测试数据)
注：在实际使用中，可能会根据需要对其中的参数进行调整。OpenCV 支持对多个参数的自定义，例如：
- 通过 setType()函数设置类别；
- 通过 setKernel()函数设置核类型；
- 通过 setC()函数设置支持向量机的参数 C（惩罚系数，即对误差的 宽容度，默认值为 0）。
属性设置代码示例：
# 2.属性设置，直接采用默认值即可
svm.setType(cv2.ml.SVM_C_SVC) # 向量机类别
# 三种常见的核是线性核函数、多项式核函数和高斯核函数
svm.setKernel(cv2.ml.SVM_LINEAR) # 线性核函数
svm.setKernel(cv2.ml.SVM_POLY) # 多项式核函数
svm.setKernel(cv2.ml.SVM_RBF) # 高斯核函数
svm.setC(0.01) # 惩罚系数，即对误差的容忍度，默认值为0（5）SVM核函数
核函数的作用就是把线性不可分的数据，从低位空间映射到高维空间，并完成分类，如下图所示：
常见的核函数有：高斯核函数、多项式核函数、线性核函数。
注：径向基函数核（Radial Basis Function, RBF kernel），也被称为高斯核（Gaussian kernel）
Openv调用方法：
- 高斯核函数：svm.setKernel(cv2.ml.SVM_RBF)
- 多项式核函数：svm.setKernel(cv2.ml.SVM_POLY)
- 线性核函数：svm.setKernel(cv2.ml.SVM_LINEAR)
（6）SVM代码实现：
"""svm_demo1.py"""
import cv2
import numpy as np
from matplotlib import pyplot as plt
def main(test):
# # 模拟数据
a = np.random.randint(0, 40, (200, 2)).astype(np.float32) # [0, 45)区间
b = np.random.randint(55, 100, (200, 2)).astype(np.float32) # [55, 100)区间
# 垂直方向合并多维数组a、b
data = np.vstack((a, b))
data = np.array(data, dtype='float32')
# # 分组标签
label_init_a = np.zeros((200, 1))
label_init_b = np.ones((200, 1))
label = np.vstack((label_init_a, label_init_b))
label = np.array(label, dtype='int32')
# # 训练阶段
# 1.生成用于后续训练的空分类器模型。
svm = cv2.ml.SVM_create()
# 2.属性设置，直接采用默认值即可
svm.setType(cv2.ml.SVM_C_SVC) # 向量机类别
# 三种常见的核是线性核函数、多项式核函数和高斯核函数
svm.setKernel(cv2.ml.SVM_LINEAR) # 线性核函数
# svm.setKernel(cv2.ml.SVM_POLY) # 多项式核函数
# svm.setKernel(cv2.ml.SVM_RBF) # 高斯核函数
svm.setC(0.01) # 惩罚系数，即对误差的容忍度，默认值为0
# 3.开始训练
result = svm.train(data, cv2.ml.ROW_SAMPLE, label) # cv2.ml.ROW_SAMPLE: 每一条数据按行排列
# # 分类（测试）
# test = [[11. 22.] [33. 44.]] 至少两个参数！
(p1, p2) = svm.predict(test)
print("p1:", "\\n", p1, "\\n")
print("p2:", "\\n", p2)
# # 可视化结果
# scatter: 散点图
# x, y: 点的位置；点的大小；点的颜色；点的形状
# print(help(plt.scatter))
plt.scatter(a[:, 0], a[:, 1], 80, 'g', 'o')
plt.scatter(b[:, 0], b[:, 1], 80, 'b', 's')
plt.scatter(test[:, 0], test[:, 1], 150, 'r', '*')
plt.show()
return p2
>>>如有疑问，欢迎评论区一起探讨
以上是关于支持向量机SVM原理解读，以及PyQt5融合SVM的代码实现，没有公式推导（已经很成熟，很难改公式，数学专业的可以推导学习）的主要内容，如果未能解决你的问题，请参考以下文章