利用python进行探索性数据分析（EDA）：以Kaggle泰坦尼克号数据集为例
Posted JoJo的数据分析历险记
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了利用python进行探索性数据分析（EDA）：以Kaggle泰坦尼克号数据集为例相关的知识，希望对你有一定的参考价值。
利用Python进行探索性数据分析（EDA）
- 🌸个人主页：JoJo的数据分析历险记
- 📝个人介绍：小编大四统计在读，目前保研到统计学top3高校继续攻读统计研究生
- 💌如果文章对你有帮助，欢迎关注、点赞、收藏、订阅专栏
本文介绍如何利用python进行探索性数据分析
参考资料:
https://www.kaggle.com/competitions/titanic
文章目录
💮探索性数据分析
探索性数据分析（EDA） 是我们进行数据分析和很多数据挖掘比赛的第一步。当我们得到一个数据后，我们首先要分析一下这个数据的基本情况，例如哪些变量是分类型的，哪些是连续型的，它们的分布是什么情况，它们之间有什么关系，数据缺失值如何。通过探索性数据分析后，我们能大致了解数据，从而进行相关模型建立以及作为特征工程的基础。
本文通过Kaggle泰坦尼克号数据来进行探索性数据分析实战。当然也有一些简单的方法得到一个简略的探索性数据分析结果，在后续我会分享给大家。
🏵️1. Titanic原始数据解读
泰坦尼克号的沉没是历史上最知名的沉船事故之一。1912年4月15日，泰坦尼克号在与冰山相撞后沉没，2224名乘客和船员中有1502人死亡。这是一场世界上任何人都无法忘记的难以忘怀的灾难。建造泰坦尼克号花费了大约750万美元，但是由于这场意外，它沉到了海底。泰坦尼克号数据集对于初学者来说是一个非常好的数据集，数据包含训练集和测试集，数据集链接我会放在文末。欢迎大家下载学习
其包含的变量如下：
变量 意义 取值
survival 是否存活 0 = No, 1 = Yes
pclass 票的种类 1 = 1st, 2 = 2nd, 3 = 3rd
sex 性别
Age 年龄(岁)
sibsp 兄弟姐妹/配偶的同行人数
parch 父母/孩子的同行人数
ticket 票号
fare 票价
cabin 座舱号
embarked 登船港口 C = Cherbourg, Q = Queenstown, S = Southampton
上述变量的一些说明：
pclass：可以看做是社会经济地位的代表
- 1=上层阶级
- 2=中层阶级
- 3=底层阶级
Age：如果小于1，则年龄为分数。如果年龄是估计的，则以xx.5的形式表示
sibsp:表示如下家庭关系
- Sibling:兄弟姐妹
- Souse:表示配偶（未婚和情人不算）
parch: 表示如下家庭关系：
- Parent：父母
- chile：孩子
好了，根据上述分析，我们对数据有哪些变量有了初步了解了，接下来我们正式进入探索性数据分析
🌹2.数据导入
首先要导入相关库，如果对以下库有不了解的可以看我本专栏之前的文章
导入相关库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('fivethirtyeight')#图形主题
import warnings
warnings.filterwarnings('ignore')#忽视警告
%matplotlib inline
分别导入训练集和测试集
df_train = pd.read_csv('train.csv')
df_test = pd.read_csv('test.csv')
🥀3.检查数据
上述我们已经导入了数据集，接下来我们来看一下该数据的一些基本情况
总览一下数据
df_train.head()
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
df_test.head()
| PassengerId | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 892 | 3 | Kelly, Mr. James | male | 34.5 | 0 | 0 | 330911 | 7.8292 | NaN | Q |
| 1 | 893 | 3 | Wilkes, Mrs. James (Ellen Needs) | female | 47.0 | 1 | 0 | 363272 | 7.0000 | NaN | S |
| 2 | 894 | 2 | Myles, Mr. Thomas Francis | male | 62.0 | 0 | 0 | 240276 | 9.6875 | NaN | Q |
| 3 | 895 | 3 | Wirz, Mr. Albert | male | 27.0 | 0 | 0 | 315154 | 8.6625 | NaN | S |
| 4 | 896 | 3 | Hirvonen, Mrs. Alexander (Helga E Lindqvist) | female | 22.0 | 1 | 1 | 3101298 | 12.2875 | NaN | S |
看一下数据的纬度
df_train.shape,df_test.shape
((891, 12), (418, 11))
可以看出训练集数据包含了891行，12列数据,测试集包含418个行11列，其中Survived列是我们要进行预测的变量
df_train.isnull().sum(),df_test.isnull().sum()
(PassengerId 0
Survived 0
Pclass 0
Name 0
Sex 0
Age 177
SibSp 0
Parch 0
Ticket 0
Fare 0
Cabin 687
Embarked 2
dtype: int64,
PassengerId 0
Pclass 0
Name 0
Sex 0
Age 86
SibSp 0
Parch 0
Ticket 0
Fare 1
Cabin 327
Embarked 0
dtype: int64)
从结果来看，训练集中age,cabin,embarked有缺失值，测试集中age,cabin,Cabin有缺失值，我们待会儿对其进行相应处理
接下来我们先看一下训练集中有多少人存活了
f,ax=plt.subplots(1,2,figsize=(18,8))
df_train['Survived'].value_counts().plot.pie(explode=[0,0.1],autopct='%1.1f%%',ax=ax[0],shadow=True)
ax[0].set_title('Survived')
ax[0].set_ylabel('')
sns.countplot('Survived',data=df_train,ax=ax[1])
ax[1].set_title('Survived')
plt.show()
很明显，幸存率很低。在训练集的891名乘客中，只有大约350人幸存，即只有38.4%幸存，说明响应变量是非平衡的，我们需要进一步挖掘哪些类别的乘客存活了，这在后续的数据挖掘项目实战中会进行相关介绍。在这里我们可以将这个38.4%当做存活率的一个先验概率
🌺4. 特征分析
除去乘客编号和姓名外一共包含十个特征变量，主要可以分为以下四种类型
🌻4.1 分类性变量（名义变量）分析
分类变量是指具有两个或多个类别的变量，该特征中的每个值都可以根据它们进行分类。例如，性别是一个分类变量，有两个类别（男性和女性）。并且我们不能对这些变量没有先后顺序。它们也被称为名义变量。
例如：sex和Embarked
🌼4.1.1 性别变量分析
下面我们以sex为例来分析一下
首先进行按性别分组,分析一下不同性别，存活率是否有差异
df_train.groupby(['Sex','Survived'])['Survived'].count()
Sex Survived
female 0 81
1 233
male 0 468
1 109
Name: Survived, dtype: int64
f,ax=plt.subplots(1,2,figsize=(18,8))
# 绘制不同性别下平均幸存率
df_train[['Sex','Survived']].groupby(['Sex']).mean().plot.bar(ax=ax[0])
ax[0].set_title('Survived vs Sex')
# 绘制不同性别下，存货和死亡的人数
sns.countplot('Sex',hue='Survived',data=df_train,ax=ax[1])
ax[1].set_title('Sex:Survived vs Dead')
plt.show()
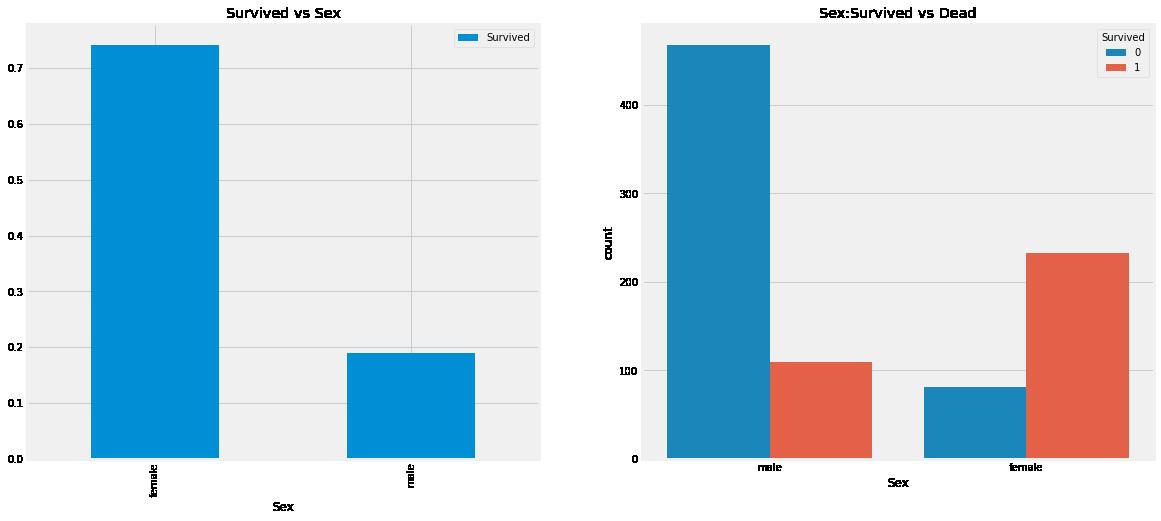
从结果来看发现一个很有趣的现象，船上的男人比女人多得多，不过，女性获救的人数几乎是男性获救人数的两倍。船上女性的存活率约为75%，而男性的存活率约为18-19%。从结果来看，性别似乎是一个很重要的特征，但它是最重要的吗？我们继续分析一下其他变量的情况
🎄4.1.2 登船港口分析
f,ax=plt.subplots(2,2,figsize=(20,15))
df_train[['Embarked','Survived']].groupby(['Embarked']).mean().plot.bar(ax=ax[0,0])
ax[0,0].set_title('Survived vs Embarked')
sns.countplot('Embarked',hue='Survived',data=df_train,ax=ax[0,1])
ax[0,1].set_title('Embarked:Survived vs Dead')
sns.countplot('Embarked',hue='Survived',data=df_train,ax=ax[1,0])
ax[1,0].set_title('Embarked vs Survived')
sns.countplot('Embarked',hue='Pclass',data=df_train,ax=ax[1,1])
ax[1,1].set_title('Embarked vs Pclass')
plt.subplots_adjust(wspace=0.2,hspace=0.5)
plt.show()
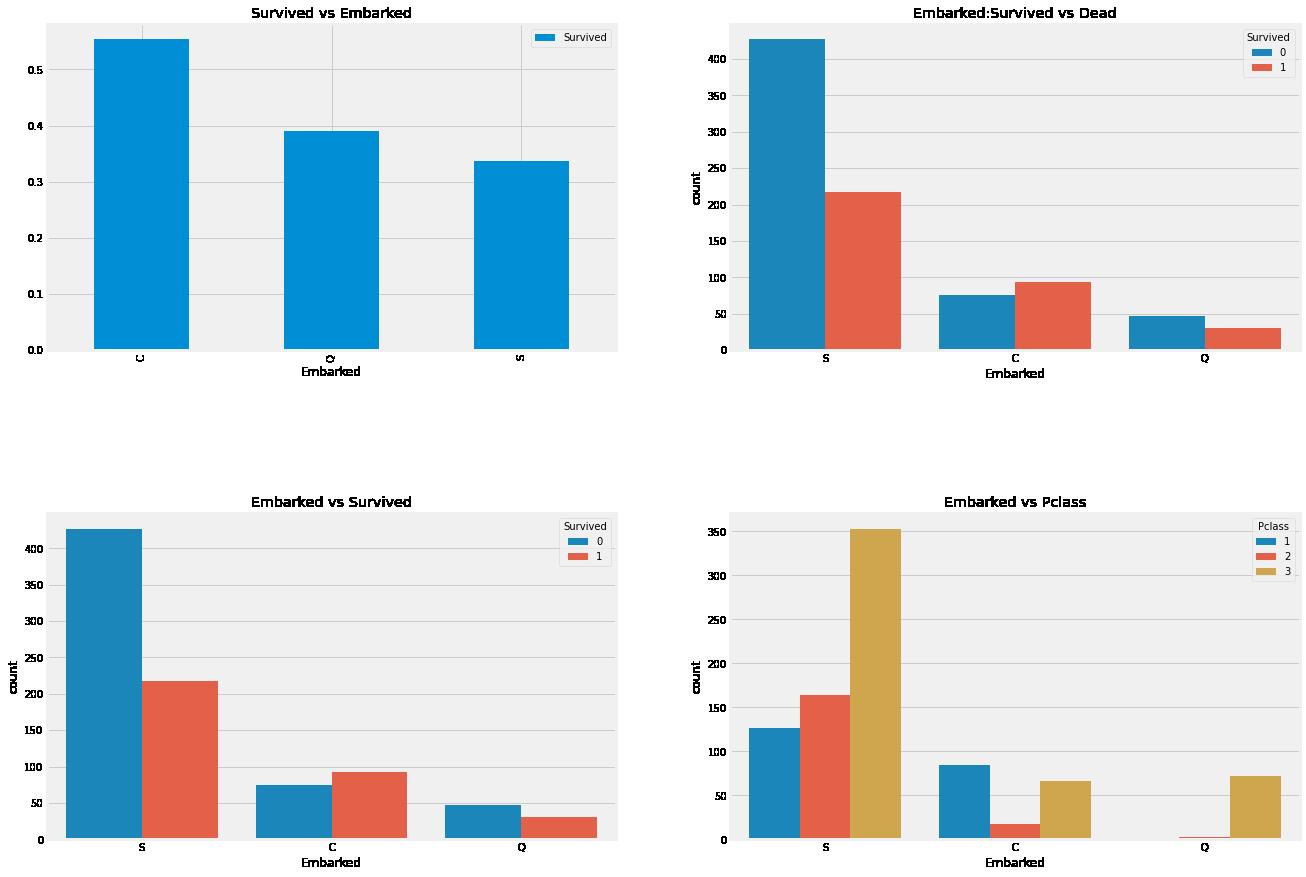
- 从S登船的旅客人数最多
- 来自C的乘客看起来很幸运，因为他们中有很大一部分幸存了下来。原因可能是营救了所有的Pclass1和Pclass2乘客。
- Q港有将近95%的乘客来自Pclass3。
从不同登船港口来看，只有C港口的存活人数比死亡人数多。
sns.factorplot('Pclass','Survived',hue='Sex',col='Embarked',data=df_train)
plt.show()
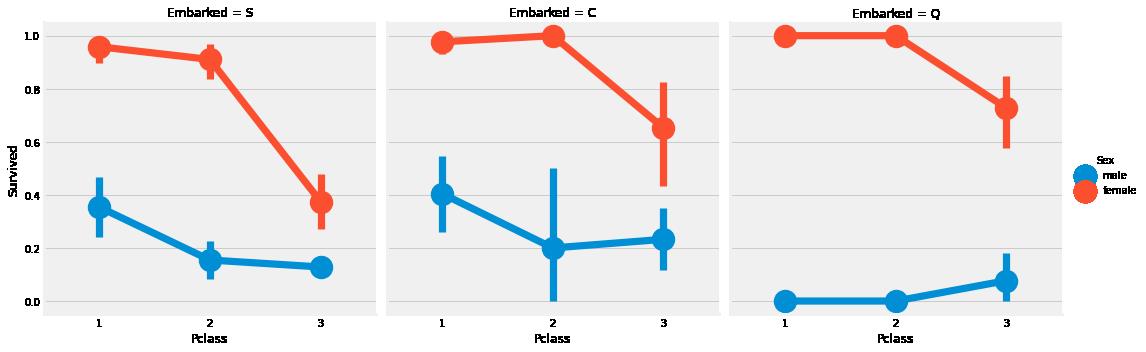
- 对于
Pclass1和Pclass2的女性来说，她们的存活几率几乎为1。 - S港对于
Pclass3乘客来说似乎非常不幸，因为男性和女性的存活率都非常低。 - Q港看起来对男性来说是最不幸运的，因为几乎所有人都来自Pclass3。
还记得我们之前发现该变量存在缺失值，我们看到从S港登机的乘客最多时，因此在这里我们用S代替了NaN。
df_train['Embarked'].fillna('S',inplace=True)
🌷4.2 定序变量分析
有序变量与分类变量类似，但它们之间的区别在于，我们可以对值进行相对排序。例如：如果我们有一个像高度这样的特征，其值为高、中、短，那么高度是一个顺序变量。在这里，我们可以对变量进行相对排序。
例如：PClass
我们之前讲过Pclass可以看做是社会地位的体现
pd.crosstab(df_train.Pclass,df_train.Survived,margins=True).style.background_gradient()
| Survived | 0 | 1 | All |
|---|---|---|---|
| Pclass | |||
| 1 | 80 | 136 | 216 |
| 2 | 97 | 87 | 184 |
| 3 | 372 | 119 | 491 |
| All | 549 | 342 | 891 |
f,ax=plt.subplots(1,2,figsize=(18,8))
df_train['Pclass'].value_counts().plot.bar(ax=ax[0])
ax[0].set_title('Number Of Passengers By Pclass')
ax[0].set_ylabel('Count')
sns.countplot('Pclass',hue='Survived',data=df_train,ax=ax[1])
ax[1].set_title('Pclass:Survived vs Dead')
plt.show()
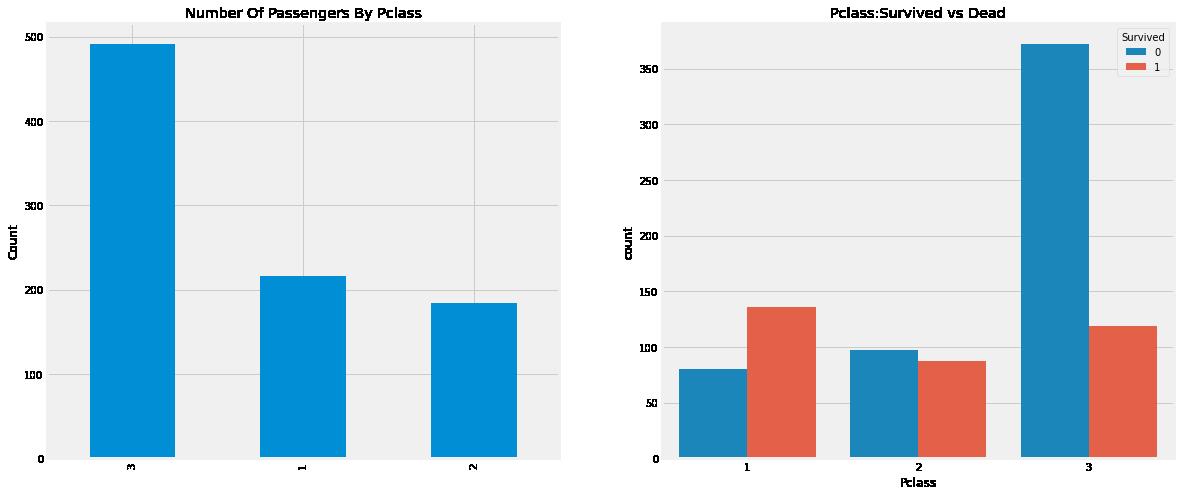
从结果可以看出一个很现实的问题，我们常说金钱买不到一切。但我们可以清楚地看到，在救援过程中，第一类乘客被给予了非常高的优先级。尽管第三类乘客的数量要高得多，但他们的存活率仍然很低，大约在25%左右。Pclass 1，存活率约为63%，而Pclass 2，存活率约为48%。 在这样一个物质世界，可以看出金钱和地位也很重要。
我们再将性别和票类型一起分析
pd.crosstab([df_train.Sex,df_train.Survived],df_train.Pclass,margins=True).style.background_gradient(cmap='summer_r')
| Pclass | 1 | 2 | 3 | All | |
|---|---|---|---|---|---|
| Sex | Survived | ||||
| female | 0 | 3 | 6 | 72 | 81 |
| 1 | 91 | 70 | 72 | 233 | |
| male | 0 | 77 | 91 | 300 | 468 |
| 1 | 45 | 17 | 47 | 109 | |
| All | 216 | 184 | 491 | 891 |
sns.factorplot('Pclass','Survived',hue='Sex',data=df_train)
plt.show()
在这种情况下，我们使用FactorPlot，因为它使分类值的分离变得容易。
现在我们来看看交叉表和因子图，可以看出，Pclass1组女性的存活率约为95-96%，在94名Pclass1组女性中，只有3人死亡。同样，无论Pclass如何，女性在救援时都被放在第一位。即使是来自Pclass1的男性，存活率也很低。
🌱4.3 连续型变量分析
如果变量可以取变量列中的最小值或最大值之间的值，则称变量为连续的。
例如：age和pare
🌲4.3.1 age
首先我们来看age的分布情况
df_train['Age'].describe()
count 714.000000
mean 29.699118
std 14.526497
min 0.420000
25% 20.125000
50% 28.000000
75% 38.000000
max 80.000000
Name: Age, dtype: float64
最大80岁，最小的才0.42岁（这里是根据天数来划分成分数的），下面我们来看一下不同性别，不同票型年龄的分布
f,ax=plt.subplots(1,2,figsize=(18,8))
sns.violinplot("Pclass","Age", hue="Survived", data=df_train,split=True,ax=ax[0])
ax[0].set_title('Pclass and Age vs Survived')
ax[0].set_yticks(range(0,110,10))
sns.violinplot("Sex","Age", hue="Survived", data=df_train,split=True,ax=ax[1])
ax[1].set_title('Sex and Age vs Survived')
ax[1].set_yticks(range(0,110,10))
plt.show()
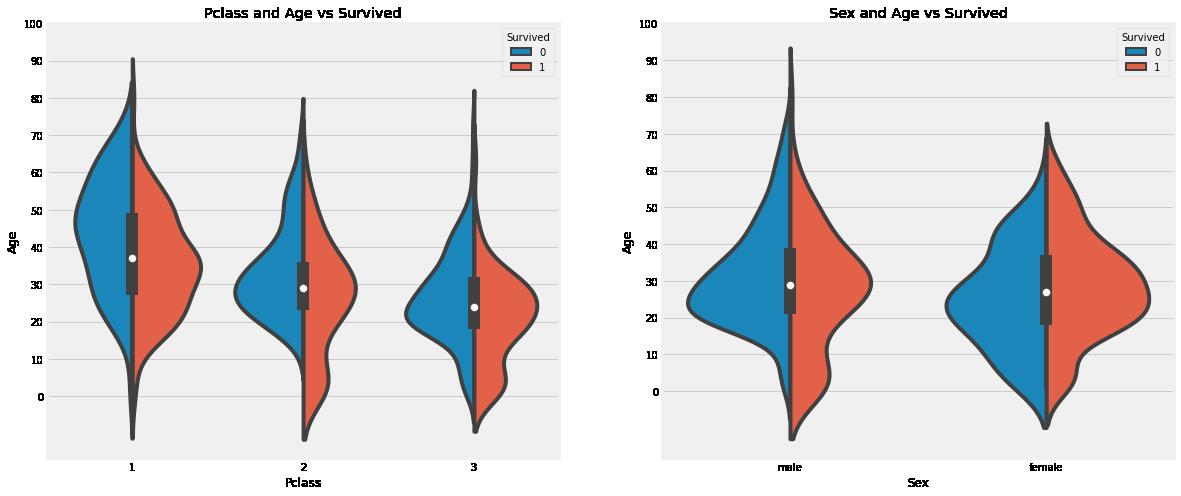
- 1） 孩子的数量随着pclass的增加而增加，但无论哪一类10岁以下的乘客（即儿童）的存活率较高。
- 2） 来自Pclass1的20-50岁乘客的生存机会很高，甚至比女性更高。
- 3） 对于男性来说，随着年龄的增长，存活的几率会降低。
正如我们之前看到的，年龄特征有177个空值。要替换这些NaN值，我们可以为它们指定数据集的平均年龄。但问题是，有很多不同年龄的人。我们不能将一个原本是50岁的人定义为4岁的孩子。有没有办法找出乘客的年龄段？我们再来看一下我们的数据集
df_train.head()
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
注意，有名字这一列，我们可以看到这些名字有一个类似Mr或Mrs的称呼，因此我们可以将Mr和Mrs的平均年龄值分配给相应的组。
首先我们通过正则表达式将这些Miss，Mr，Mrs提取出来,放在Initial列中
df_train['Initial']=0
for i in df_train:
df_train['Initial']=df_train.Name.str.extract('([A-Za-z]+)\\.')
我们使用了[A-Za-z]+)\\ .所以它所做的是，它寻找A-Z或a-z之间的字符串，后面跟着.所以我们成功地从名字中提取了我们想要的信息
df_train.head()
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | Initial | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S | Mr |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C | Mrs |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S | Miss |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S | Mrs |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S | Mr |
pd.crosstab(df_train.Initial,df_train.Sex).T.style.background_gradient(cmap='summer_r') #Checking the Initials with the Sex
| Initial | Capt | Col | Countess | Don | Dr | Jonkheer | Lady | Major | Master | Miss | Mlle | Mme | Mr | Mrs | Ms | Rev | Sir |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sex | |||||||||||||||||
| female | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 182 | 2 | 1 | 0 | 125 | 1 | 0 | 0 |
| male | 1 | 2 | 0 | 1 | 6 | 1 | 0 | 2 | 40 | 0 | 0 | 0 | 517 | 0 | 0 | 6 | 1 |
有一些拼写错误的首字母，比如Mlle或Mme，代表Miss。我将用Miss来进行替换，具体如下所示
df_train['Initial'].replace(['Mlle','Mme','Ms','Dr','Major','Lady','Countess','Jonkheer','Col','Rev','Capt','Sir','Don'],['Miss','Miss','Miss','Mr','Mr','Mrs','Mrs','Other','Other','Other','Mr','Mr','Mr'],inplace=True)
此时再计算每一类的平均年龄
df_train.groupby('Initial')['Age'].mean()
Initial
Master 4.574167
Miss 21.860000
Mr 32.739609
Mrs 35.981818
Other 45.888889
Name: Age, dtype: float64
根据这些平均年龄对每一类的缺失值填充
df_train.loc[(df_train.Age.isnull())&(df_train.Initial=='Mr'),'Age']=33
df_train.loc[(df_train.Age.isnull())&(df_train.Initial=='Mrs'),'Age']=36
df_train.loc[(df_train.Age.isnull())&(df_train.Initial=='Master'),'Age']=5
df_train.loc[(df_train.Age.isnull())&(df_train.Initial=='Miss'),'Age']=22
df_train.loc[(df_train.Age.isnull())&(df_train.Initial=='Other'),'Age']=46
我们再来看看年龄的缺失值情况
df_train.Age.isnull().sum()
0
下面我们再来看一下幸存和死亡人员的年龄分布
f,ax=plt.subplots(1,2,figsize=(20,10))
df_train[df_train['Survived']==0].Age.plot.hist(ax=ax[0],bins=20,edgecolor='black',color='red')
ax[0].set_title('Survived= 0')
x1=list(range(0,85,教程 | 如何利用散点图矩阵进行数据可视化
python进行探索性数据分析EDA（Exploratory Data Analysis）分析
探索性数据分析 (EDA)，Python 中这 4 个方法更快真棒
手把手教学：使用Elastic search和Kibana进行数据探索（Python语言）
什么是探索性数据分析EDA（Exploratory Data Analysis）？，探索性数据分析EDA（Exploratory Data Analysis）对机器学习有是意义？探索性数据分析EDA详