AlexNet架构重现与解析

Posted 2022-04-13 mini梁翊洲MAX

这篇文章，我们将开始讨论深度学习——计算机视觉的一个重要工具。我会以经典网络架构为切入点，来深入理解深度学习中各部分的功能以及原理。由于这是第一篇，所以会涉及许多基础的知识，后面就不会重复已经讲过的知识。

在开始之前，我想先说一点。深度学习许多东西的理论性并不好，许多参数的选择都是无数次的实验比较出来的。这种比较实验的思想也应该是以后我们选择不同模型时应该遵循和参考的依据。

导入需要的库

import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib
import matplotlib.pyplot as plt
import random
import cv2
from keras.models import Sequential
from keras.layers import Conv2D
from keras.layers import MaxPooling2D
from keras.layers import Activation
from keras.layers import Flatten
from keras.layers import Dense
from keras.layers import Dropout
from keras.initializers import RandomNormal
from keras.initializers import Zeros
from keras.initializers import Ones
from tensorflow.keras.utils import to_categorical
from keras import backend as K
from keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.optimizers import SGD
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from keras.preprocessing.image import img_to_array
from imutils import paths
import gc
import os

设置一些必要的参数。

We trained our models using stochastic gradient descent with a batch size of 128 examples, momentum of 0.9, and weight decay of 0.0005.
The learning rate was initialized at 0.01 and reduced three times prior to termination.

根据原文，我们将批量大小设置为128，初始学习率为0.01 。

matplotlib.use("Agg")
dataset="../input/flowers-recognition/flowers"
output_model="./"
plot="./"
EPOCHS=100
INIT_LR=1e-2
BS=128

批量大小 Batch Size

批量大小指一次性放入训练的数据量大小。我们评价训练结果的好坏往往根据训练误差的数值，举个经典的例子，我们一开始处于一片山林的任意位置（根据我们的初始值决定），我们的目标就是走到我们认为是最底部的山谷（训练误差最小）。

而我们每次计算训练误差时的数据，就像你的地图，记录着当前位置附近区域的陡峭程度。经过计算之后，它会告诉你前进方向，然后我们会往这个方向前进一步（学习率）。而数据量的多少，即批量大小可能会影响你“视野”的范围。

假设我们以上帝视角观察这位在山谷中行走的人，当他每次训练误差的数据很大时，我们可以看到他是沿着坡度最陡的路直接走向最近的山谷。而有着小批量的人，他可能也是到达同一个目的地，但其行走的方向是一会向东一会向西，歪歪扭扭的。

我们很容易理解为什么小批量会导致这种现象，因为它每次训练的数据只是部分的，所以其视野也是有着局限的，只能感受到部分区域的陡峭程度。但因为其数据量小，所以虽然不是沿着整体最陡路径走，但它每一步的速度都很快，一般会更快地到达山谷。

另外，有人通过实验发现，小批量数据得到的结果往往更好。对此，我觉得一个比较能接受的解释是，小批量受噪声影响更多（大批量受噪声影响小是因为噪声会叠加互相抵消），导致其前行方向多变。我们都知道，有时候我们会陷入局部最优解，而小批量导致的前进方向多变性可能导致其无意间进入山脊，它可能就会滑向另一个更好的最优解。支撑这一观点的数据主要是不同批量数据的训练过程距离初始点的位置。经过实验发现，小批量往往远离初始点，即可能脱离了初始点区域的局部最优解。

大批量一定是不好的吗？其实调整学习率可以消除小批量和大批量之间的大部分性能差距。每个批量都有一个对应的最佳学习率，整体是呈线性关系，但具体取值我认为和模型以及数据有关，我无法给出一个通解，所以如果想尽可能优化方案的话，不妨做些对比实验。

初始学习率 Learning Rate

通常我们会尝试性的将初始学习率设为：0.1，0.01，0.001，0.0001 。如果训练初期loss下降缓慢，说明初始学习率偏小。如果训练初期loss出现梯度爆炸或NaN这样的情况，说明初始学习率偏大。如果训练一段时间后loss下降缓慢或者出现震荡现象，可能训练进入到一个局部最小值需要降低学习率使训练朝更精细的位置移动，文中作者就降低了三次学习率。

reduced three times prior to termination.

初始学习率的选取也可以考虑Batch Size的影响，正如上文所说。但我不建议训练全程保持同一个学习率。在我们复现的代码中，我们没有对学习率进行手动的修改，但引入了衰减，后面我们会看到。

导入打乱顺序的训练数据，并把图片resize为同一尺寸，因为我们模型的输入尺寸必须固定。

data=[]
labels=[]

imagePaths=sorted(list(paths.list_images(dataset)))
random.seed(27)
random.shuffle(imagePaths)


for imagePath in imagePaths:
    image=cv2.imread(imagePath)
    image=cv2.resize(image,(227,227))
    image=img_to_array(image)
    data.append(image)
    
    label=imagePath.split(os.path.sep)[-2]
    labels.append(label)

We do this by extracting random 224 × 224 patches (and their horizontal reflections) from the 256×256 images and training our network on these extracted patches

在原文中，作者会从四个角和中间分别裁剪出特定尺寸的图像（以及它们的水平翻转）。这是数据增强的一种方法，但请允许我忽略裁剪这一步操作，这实在是有点麻烦，关于数据增强我们后面会有一个更简便的方法。

我们将训练数据转换格式，并分成训练集和验证集。在这里我们可以看到，我是如何删除一些大的变量以确保我RAM内存充足的，如果不这样做我甚至没有空间训练模型。

我们还将标签转换成独热码的形式，方便后续多分类。

data=np.array(data,dtype="float")
labels=np.array(labels)
labels=labels.flatten()
le = LabelEncoder()
labels = le.fit_transform(labels)

(trainX,testX,trainY,testY)=train_test_split(data,labels,test_size=0.3,random_state=27)

del data,labels,imagePaths
gc.collect()

trainY=to_categorical(trainY,num_classes=5)
testY=to_categorical(testY,num_classes=5)

数据增强

这个ImageDataGenerator（）就是常用的数据增强的函数。

aug = ImageDataGenerator(width_shift_range=0.1,
height_shift_range=0.1,horizontal_flip=True, 
fill_mode="nearest")

The first form of data augmentation consists of generating image translations and horizontal reflections.

根据原文的描述，我们这里只进行了平移和水平翻转。但其实这个函数还可以做很多事情，因为它仅仅是一些参数，所以我也不赘述，大家可以查阅相关资料。

数据增强往往是通过对源图像进行一系列操作，来模拟不同角度不同方式拍摄同一个物体，在扩充了数据集的同时也提高了泛化能力。

文中还提到了另一种数据增强的方法，不过我没太懂。

he second form of data augmentation consists of altering the intensities of the RGB channels in training images.

接下来是我们的模型主题架构。

class AlexNet:
    def build(width,height,depth,classes):
        model=Sequential()
        
        inputShape=(height,width,depth)
        if K.image_data_format()=="channels_first":
            inputShape=(depth,height,width)
            
        model.add(Conv2D(96,(11,11),strides=(4,4),input_shape=inputShape,kernel_initializer=RandomNormal(mean=0.0, stddev=0.01),bias_initializer=Zeros))
        model.add(Activation("relu"))
        model.add(MaxPooling2D(pool_size=(3,3),strides=(2,2)))
        
        model.add(Conv2D(256,(5,5),padding="same",kernel_initializer=RandomNormal(mean=0.0, stddev=0.01),bias_initializer=Ones))
        model.add(Activation("relu"))
        model.add(MaxPooling2D(pool_size=(3,3),strides=(2,2)))
        
        model.add(Conv2D(384,(3,3),padding="same",kernel_initializer=RandomNormal(mean=0.0, stddev=0.01),bias_initializer=Zeros))
        model.add(Activation("relu"))
        
        model.add(Conv2D(384,(3,3),padding="same",kernel_initializer=RandomNormal(mean=0.0, stddev=0.01),bias_initializer=Ones))
        model.add(Activation("relu"))
        
        model.add(Conv2D(256,(3,3),padding="same",kernel_initializer=RandomNormal(mean=0.0, stddev=0.01),bias_initializer=Ones))
        model.add(Activation("relu"))
        model.add(MaxPooling2D(pool_size=(3,3),strides=(2,2)))
        
        model.add(Flatten())
        model.add(Dense(4096,kernel_initializer=RandomNormal(mean=0.0, stddev=0.01),bias_initializer=Ones))
        model.add(Activation("relu"))
        model.add(Dropout(0.5))
        
        model.add(Dense(classes*100,kernel_initializer=RandomNormal(mean=0.0, stddev=0.01),bias_initializer=Ones))
        model.add(Activation("relu"))
        model.add(Dropout(0.5))
        
        model.add(Dense(classes,kernel_initializer=RandomNormal(mean=0.0, stddev=0.01),bias_initializer=Ones))
        model.add(Activation("softmax"))
        
        return model

在正式展开讲解之前，我先说明这里的理论性会比较差。人们选择的时候往往是在经验的基础上加大量实验，如果对选择的详细过程好奇的话，可以在评论区留言，我就会详细介绍实验选择的流程。

卷积核

卷积核大小：11-5-3-3-3 。 AlexNet一开始是用了一个11的大卷积核，他没有说明具体原因，我们可以推测看看。在当时的主流思想看来，大卷积核一次能感受到的视野是更多的，这当然没错，作者当时想的可能也是第一层主要就抓取整体轮廓特征。但是，经过我们后来分析，多个小的卷积核叠加也能感受到同样大的视野，而且计算复杂度会大大减小。至于多小是合适的，就取决于训练的图像了。如果卷积核太小，导致大部分卷积核都没能覆盖到我们想提取的特征，那完全就是做了无用功。后面的几个大小都中规中矩，也是我们一般会设置的值。

步长：4-1-1-1-1 。之所以第一个步长较大是因为第一层卷积核比较大，和感受视野有关。

this is the distance between the receptive field centers of neighboring neurons in a kernel map

关于步长，没有一个明确的通用方案。我姑且给出我自己直观的判断。对于大的卷积核，如果步长设置的过小，那么相邻两个卷积核的输出高度一致，为了避免做太多无用功，我们会将步长设置得稍微大点。现在，我们得卷积核一般都是比较小的，步长一般也默认为1 。但是，我们也可以有自己的判断标准，对于要学习的内容比较复杂的对象，我们的步长可以尽可能小，因为即使有大量重叠，但因为复杂程度高我们也能学习到不同的特征。对于不那么复杂的对象，我们就可以将步长设置得大一点。

卷积核数量：96-256-384-384-256 。这里面确实没啥文章可作，我们不妨给它一个规律。网络越深，图像被提取凝练后变得越小，卷积核数量越多。当然，这并不是绝对的。

填充： padding我们默认填充0。之所以要进行填充操作是有两个原因。一是卷积多次后图像会变得非常小，二是不填充卷积时容易丢失图片边缘信息。那么是否一定padding？我觉得如果你能确定你想获取的特征不在图像边缘，那么在前面我们可以不用padding。在后期我们是必须padding的，否则将会丢失非常多的信息。

重叠池化层

作者说他是在训练过程中发现重叠池化层比传统的池化层更能降低过拟合的影响。具体解释我也没什么头绪。

We generally observe during training that models with overlapping pooling find it slightly more difficult to overfit.

ReLU

使用非线性激活函数是为了增加神经网络模型的非线性因素，以便使网络更加强大，增加它的能力，使它可以学习复杂的事物，复杂的表单数据，以及表示输入输出之间非线性的复杂的任意函数映射。

Deep convolutional neural networks with ReLUs train several times faster than their equivalents with tanh units.

ReLU相对于当时另外两个经典激活函数来说，有着收敛速度快，计算简单，不会出现梯度饱和、梯度消失的优点。但它同时也存在死区的问题，在x<0时，梯度为0。这个神经元及之后的神经元梯度永远为0，不再对任何数据有所响应，导致相应参数永远不会被更新。在我第一次训练时，就将像素缩放到[0,1],学习率设的也比较大，导致无论怎么训练都没有效果。

高斯分布初始化权值

使用高斯分布对每个参数随机初始化。关键是设置方差，如果太小，后续输出信号可能就消失了。太大可能会导致梯度爆炸（对于sigmoid）。一般我们需要搭配逐层归一化一起使用，但是这里作者没有使用。

现在人们对于激活函数为ReLU的模型，更倾向于用He初始化。

We initialized the weights in each layer from a zero-mean Gaussian distribution with standard deviation 0.01.

偏置值初始化

We initialized the neuron biases in the second, fourth, and fifth convolutional layers, as well as in the fully-connected hidden layers, with the constant 1. This initialization accelerates the early stages of learning by providing the ReLUs with positive inputs. We initialized the neuron biases in the remaining layers with the constant 0.

与我们平时直接偏置设为0不同，作者把部分设为了1 。作者认为这样子可以使部分小于0的输入变成正值，从而移除了ReLU的死区，在前期帮助加速学习。

Softmax

这个是几乎所有关于分类问题中，模型最后一步都有做的。其具体操作是将训练得出的n个结果，缩放到[0,1]之间。全部结果加起来等于1，其实就相当于每个结果对应的概率。

赋予模型参数，设置优化器。

model=AlexNet.build(width=227,height=227,depth=3,classes=5)
opt = SGD(learning_rate=INIT_LR, momentum=0.9, decay=0.0005)
model.compile(loss="categorical_crossentropy",
optimizer=opt,metrics=["accuracy"])

随机梯度下降 SGD

这个的形象描述在上面的BS里已经说过了，这里我针对里面的参数设计到的新的概念进行一下阐述。

动量 momentum：理解这个也不难，它类比于我们现实生活中的惯性。我们可以想象一个小球滚到了一个小山坡，如果没有动量，此时因为梯度为0，小球就躺在那里不动了。但是现实中，小球由于惯性作用会沿原方向继续运动一段距离，即爬坡，如果到达最高点还没爬出这个山坡，就会慢慢滚回去直到停在坡里。但如果这个山坡很小很平滑，依靠这个惯性小球可能离开这个山坡去寻找下一个山坡。这就一定几率避免了我们陷于局部最优解的困境。

衰减率 decay：学习率 = 学习率 * 1/(1 + 衰减率* 训练次数)。我们可以看到学习率不是维持在初始学习率，而是随着训练次数而逐渐减小的。在前文我们已经知道在前期大的学习滤波有助于我们快速训练，在后期小的学习率更有助于我们找到合适的最优解。

多分类损失函数 categorical_crossentropy

分类问题搭配softmax使用，其原理涉及信息熵等概念，讲起来比较复杂。感兴趣的可自行搜索。使用时没有什么参数要调，所以遇到多分类问题直接使用就可以。

训练数据

H = model.fit(x=aug.flow(trainX, trainY, batch_size=BS),
    validation_data=(testX, testY), 
    steps_per_epoch=len(trainX) // BS,
    epochs=EPOCHS, verbose=1)

绘画训练过程

plt.style.use("ggplot")
fig=plt.figure()
N = EPOCHS
plt.plot(np.arange(0, N), H.history["loss"], label="train_loss")
plt.plot(np.arange(0, N), H.history["val_loss"], label="val_loss")
plt.plot(np.arange(0, N), H.history["accuracy"], label="train_acc")
plt.plot(np.arange(0, N), H.history["val_accuracy"], label="val_acc")
plt.title("Training Loss and Accuracy")
plt.xlabel("Epoch #")
plt.ylabel("Loss/Accuracy")
plt.legend(loc="lower left")
fig

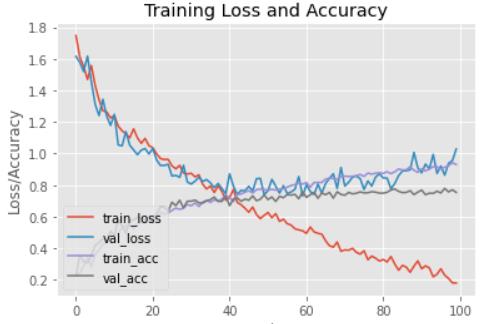
这是kaggle的一个花分类的数据集。利用AlexNet训练，训练精确度后期接近百分之九十，而且仍在上升。交叉验证精度在0.75左右开始波动，上升缓慢。

与50位技术专家面对面 20年技术见证，附赠技术全景图