207. 课程表-找环BFS

Posted 2022-04-13 hequnwang10

一、题目描述

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

• 例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

二、解题

BFS

这题使用广度优先遍历，拓扑排序。将入度为0的节点入队，然后出队，其他节点与当前节点相连接的入度-1；依次遍历即可。

class Solution 
    public boolean canFinish(int numCourses, int[][] prerequisites) 
        //邻接表
        List<List<Integer>> edges = new ArrayList<>();
        //每个点的入度，点是[0,n-1];
        int[] indegree = new int[numCourses];
        //初始化每个点的邻接表
        for(int i = 0;i<numCourses;i++)
            edges.add(new ArrayList<Integer>()); 
        
        //初始化每个点入度
        for(int[] info : prerequisites)
            //[1,0]先学习后面的课程0，然后才能在学现在的课程1;
            //创建连接表,在info[1]对应的位置,放入后连接的一个数字也就是info[0],
            edges.get(info[1]).add(info[0]);
            //节点1的入度+1；
            indegree[info[0]]++;
        

        //将度为0的点入队列
        Queue<Integer> queue = new LinkedList<>();
        for(int i = 0;i<numCourses;i++)
            if(indegree[i] == 0)
                queue.add(i);
            
        
        while(!queue.isEmpty())
            //将队列中入度为0的节点出队，访问这个节点的邻接表，将其他点的入度-1；
            int cur = queue.poll();
            numCourses--;
            for(int v : edges.get(cur))
                //将v的这个节点的入度-1；
                indegree[v]--;
                //如果这个节点的入度为0 入队
                if(indegree[v] == 0)
                    queue.add(v);
                
            
        
        return numCourses == 0;  
    

环判断

class Solution 
    public boolean canFinish(int numCourses, int[][] prerequisites) 
        //邻接表
        List<Integer>[] graphic = new List[numCourses];
        //初始化邻接表
        for (int i = 0; i < numCourses; i++) 
            graphic[i] = new ArrayList<>();
        
        //构建邻接表，当前节点需要后面的那个节点完成之后才能完成
        for (int[] pre : prerequisites) 
            graphic[pre[0]].add(pre[1]);
        
        boolean[] globalMarked = new boolean[numCourses];
        boolean[] localMarked = new boolean[numCourses];
        for (int i = 0; i < numCourses; i++) 
            if (hasCycle(globalMarked, localMarked, graphic, i)) 
                return false;
            
        
        return true;
    
    //判断是否有环
   private boolean hasCycle(boolean[] globalMarked, boolean[] localMarked,List<Integer>[] graphic, int curNode) 
        System.out.println("1->localMarked[curNode]："+localMarked[curNode]+" ->curNode:"+curNode);
        System.out.println("1->globalMarked[curNode]："+globalMarked[curNode]+" ->curNode:"+curNode);
        //先判断局部的节点是否被访问过，如果被访问过，说明出现环了
        if (localMarked[curNode]) 
            return true;
        
        //再继续判断全局的节点是否被访问过，被访问过，说明可以继续访问这个节点 不存在环
        if (globalMarked[curNode]) 
            return false;
        
        //将当前节点设置为访问过
        globalMarked[curNode] = true;
        localMarked[curNode] = true;
        System.out.println("2->localMarked[curNode]："+localMarked[curNode]+" ->curNode:"+curNode);
        System.out.println("2->globalMarked[curNode]："+globalMarked[curNode]+" ->curNode:"+curNode);
        for (int nextNode : graphic[curNode]) 
            //如果有环 返回true；
            if (hasCycle(globalMarked, localMarked, graphic, nextNode)) 
                return true;
            
        
        localMarked[curNode] = false;
        System.out.println("3->localMarked[curNode]："+localMarked[curNode]+" ->curNode:"+curNode);
        System.out.println("3->globalMarked[curNode]："+globalMarked[curNode]+" ->curNode:"+curNode);
        return false;
    

测试用例

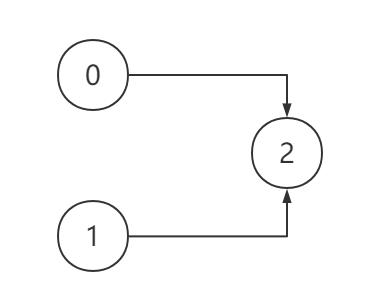
3
[[2,0],[2,1]]

1->localMarked[curNode]：false ->curNode:0
1->globalMarked[curNode]：false ->curNode:0
2->localMarked[curNode]：true ->curNode:0
2->globalMarked[curNode]：true ->curNode:0
3->localMarked[curNode]：false ->curNode:0
3->globalMarked[curNode]：true ->curNode:0
1->localMarked[curNode]：false ->curNode:1
1->globalMarked[curNode]：false ->curNode:1
2->localMarked[curNode]：true ->curNode:1
2->globalMarked[curNode]：true ->curNode:1
3->localMarked[curNode]：false ->curNode:1
3->globalMarked[curNode]：true ->curNode:1
1->localMarked[curNode]：false ->curNode:2
1->globalMarked[curNode]：false ->curNode:2
2->localMarked[curNode]：true ->curNode:2
2->globalMarked[curNode]：true ->curNode:2
1->localMarked[curNode]：false ->curNode:0
1->globalMarked[curNode]：true ->curNode:0
1->localMarked[curNode]：false ->curNode:1
1->globalMarked[curNode]：true ->curNode:1
3->localMarked[curNode]：false ->curNode:2
3->globalMarked[curNode]：true ->curNode:2