人脸识别系统FaceNet原理

Posted 2022-03-31 zhiyong_will

1. 概述

近年来，随着深度学习在CV领域的广泛应用，人脸识别领域也得到了巨大的发展。在深度学习中，通过多层网络的连接，能够学习到图像的特征表示，那么两张人脸的图像，是不是可以通过深度学习判别其是否是相同的人呢？Google在2015年提出了人脸识别系统FaceNet[1]，可以直接将人脸图像映射到欧式空间中，空间中的距离直接代表了人脸的相似度。最终，FaceNet在LFW数据集上，准确率为0.9963，在YouTube Faces DB数据集上，准确率为0.9512。FaceNet的主要优化点是：

1. 通过端到端的深度学习结构将人脸映射到同一个欧式空间中，使得在映射后欧式空间中彼此之间是可度量的；
2. 提出损失函数Triplet Loss，目标是使得相同人脸在欧式空间中距离较近，不同人脸在欧式空间中距离较远。

2. 算法原理

2.1. FaceNet

FaceNet的简单结构示意图如下所示：

在FaceNet中，并未直接使用预训练的CNN模型直接提取人脸特征，同时为了能够将人脸的图像映射到同一个欧式空间中且可度量，在FaceNet采用端对端对人脸图像直接进行学习，学习从图像到欧式空间的编码方法，然后基于这个编码再做人脸识别、人脸验证和人脸聚类等。

FaceNet的网络结构与传统的深度学习模型非常相似，不同的是在FaceNet中去掉了分类模型中中Softmax，取而代之的是L2归一化，通过L2归一化得到人脸的特征表示，直接将人脸的图像$x$映射到$d$维的欧式空间中$f\left(x\right)\in {\mathbb{R}}^d$。其中L2归一化的目的是去使得认脸的向量在同一量纲下，深度模型不是本文的重点，现如今有大量成熟的CNN模型可以直接使用，如VGG，Inception，Resnet等

2.2. Triplet Loss

Triplet Loss是FaceNet系统的另一大特点，对于认脸图像$x$，通过Triplet Loss可以使得映射后的向量表示$f\left(x\right)$在欧式空间中可以度量，Triplet Loss的目标是使得相同的人脸图像在欧式空间中的向量的欧式距离相近，不同的人脸图像在欧式空间中的向量的欧式距离较远。用数学的方式方式可以表示为：假设输出人脸图像是$x_i^a$，已称为anchor，同一个人的人脸图像$x_i^p$，也称为positive，另一个不同人的人脸图像$x_i^n$，也称为negative，需要使得$x_i^a$和$x_i^p$之间的向量距离较近，$x_i^a$和$x_i^n$之间的距离较远，即为：

$${\Vert f\left(x_i^a\right)-f\left(x_i^p\right)\Vert }_2^2+\alpha <{\Vert f\left(x_i^a\right)-f\left(x_i^n\right)\Vert }_2^2,\forall \left(f\left(x_i^a\right),f\left(x_i^p\right),f\left(x_i^n\right)\right)\in \tau$$

其中，$\alpha$是使得正（positive）负（negative）人脸充分分开的阈值，$\tau$是所有的$\left(x_i^a,x_i^p,x_i^n\right)$三元组的集合，集合的大小为$N$。训练的过程可由下图表示：

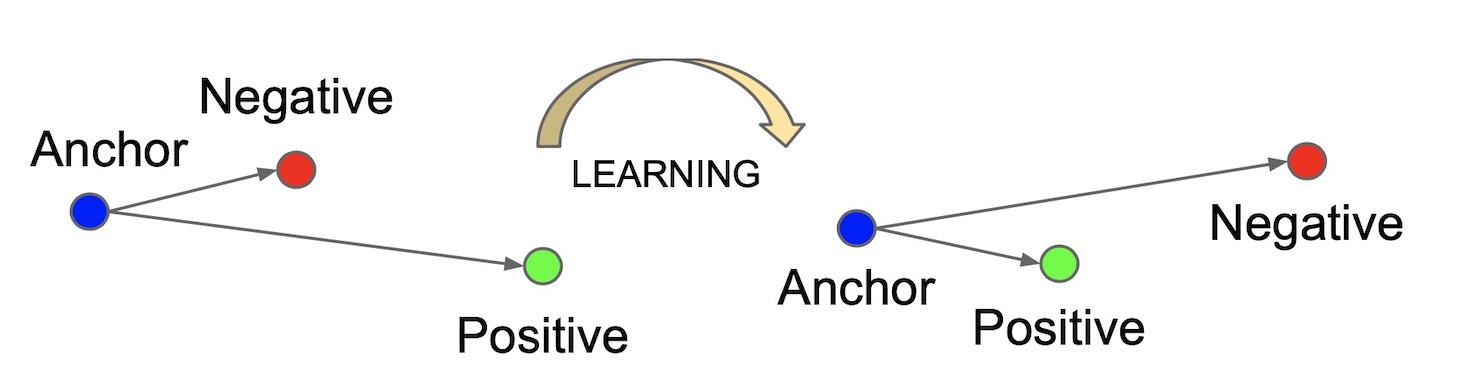
通过不断的学习，使得Anchor和Positive的距离较近，而Anchor和Negative的距离变远。对于FaceNet，其损失函数为：

$$L=\sum _i^N\left[{\Vert f\left(x_i^a\right)-f\left(x_i^p\right)\Vert }_2^2-{\Vert f\left(x_i^a\right)-f\left(x_i^n\right)\Vert }_2^2+\alpha \right]$$

2.3. 样本选择

上述三元组$\left(x_i^a,x_i^p,x_i^n\right)$构成了训练集合$\tau$，然而三原组的选择对模型的收敛非常重要。由上述公式可知，对于人脸图像$x_i^a$，需要选择同一认脸的不同图像$x_i^p$，使得

$$argma{x}_{x_i^p}{\Vert f\left(x_i^a\right)-f\left(x_i^p\right)\Vert }_2^2$$

同时，还需要选择不同认脸的图像$x_i^n$，使得

$$argmi{n}_{x_i^n}\Vert f\left(x_i^a\right)-f(x_i^n$$

facenet快速复现 实现 facenet-pytorch 人脸识别 windows上 使用cpu实现 人脸对比

使用 facenet 进行人脸识别

facenet-retinaface快速复现 实现 facenet-retinaface-pytorch 人脸识别 windows上 使用cpu实现

facenet-retinaface快速复现 实现 facenet-retinaface-pytorch 人脸识别 windows上 使用cpu实现

快速复现 实现 facenet-pytorch 人脸识别 windows上 使用cpu实现 人脸对比

人脸检测—Retinanetface