manacher最长回文字符串小y的镜像串

Posted 2022-03-29 行码棋

本篇文章不是详细讲解，如需详细讲解请跳转参考文章

Manacher问题

参考文章：

https://oi-wiki.org/string/manacher/

https://blog.csdn.net/weixin_42373330/article/details/82118694

变量描述：

$p[i]$ 以i为中心的向右可以扩展的最长回文字符串的长度

$mx$：i之前的最长回文字符串到达右边的最远边界位置

$ma[i]$:对字符串处理后的字符串，字符串处理需要在相邻两个字符之间插入#字符，以解决奇数和偶数回文的问题
以abbc为例，插入后为$#a#b#b#c#

i	0	1	2	3	4	5	6	7	8	9
s	$	#	a	#	b	#	b	#	c	#
$p[i]$	1	1	2	1	2	3	2	1	2	1

char ma[N * 2];
int p[N * 2];
void manacher(char s[], int len)

	int l = 0;
	ma[l++] = '$';
	ma[l++] = '#';
	for(int i = 0; i < len; i++)
	
		ma[l++] = s[i];
		ma[l++] = '#';
	

	ma[l] = 0;
	int mx = 0, id = 0;

	for(int i = 0; i < l; i++)
	
		p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
		while(ma[i + p[i]] == ma[i - p[i]])
			p[i] ++;
		if(i + p[i] > mx)
		
			mx = i + p[i];
			id = i;
		
	

模板题

https://www.luogu.com.cn/problem/P3805

求一个字符串的所有子串的最长回文字符串的长度

代码：

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1.2 * 1e7, M = 2 * N;

char ma[M];
int p[M];
char s[N];

void manacher(char s[], int len)

	int l = 0;
	ma[l++] = '$';
	ma[l++] = '#';
	for(int i = 0; i < len; i++)
	
		ma[l++] = s[i];
		ma[l++] = '#';
	

	ma[l] = 0;
	int mx = 0, id = 0;

	for(int i = 0; i < l; i++)
	
		p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
		while(ma[i + p[i]] == ma[i - p[i]])
			p[i] ++;
		if(i + p[i] > mx)
		
			mx = i + p[i];
			id = i;
		
	

int main()

	cin >> s;
	int len = strlen(s);
	manacher(s, len);
	int res = 0;
	for(int i = 0; i < 2 * len + 2; i++)
		res = max(res, p[i] - 1);
	cout << res << "\\n";
	return 0;

例题

题目链接
https://ac.nowcoder.com/acm/contest/30782/F
(因为是私有比赛，可能会进不去)

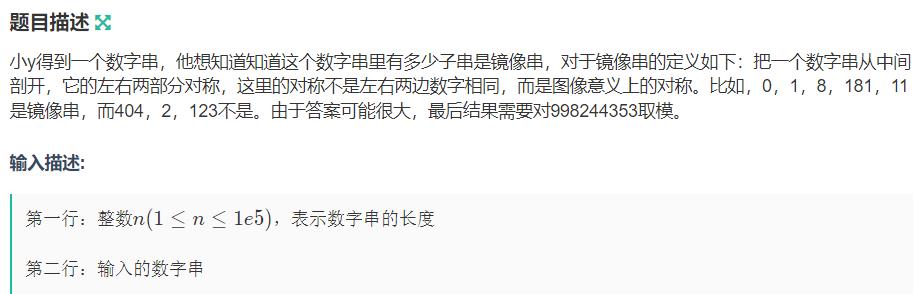
求一个字符串的所有子串的镜像串的个数

---

本题带修莫队应该是正解，但是马拉车也可以过。

利用manacher算法求出以所有点为中心的最长回文串长度，如果是字符#的话，说明该回文串为偶数，若是数字的话，说明回文串长度为奇数。

需要修改的地方为：

manacher算法时，长度扩展时，只有0,1,8字符可以扩展，其余的不可以扩展，所以要加上判断条件。

统计答案时，只有0,1,8可以统计答案，其余的不可以。

---

$p[i]$：以i为中心的最长的回文子串的长度

注意一个结论：$p[i]-1$为原字符串在回文串中的长度

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 5, mod = 998244353;

char s[N], ma[2 * N];
ll p[N * 2];

bool check(char c)

	if(c == '0' || c == '1' || c == '8' || c == '#')
		return true;
	return false;

void manacher(char s[], int len)

	int l = 0;
	ma[l ++] = '$';
	ma[l ++] = '#';
	for(int i = 1; i <= len; i++)
	
		ma[l++] = s[i];
		ma[l++] = '#';
	
	ma[l] = 0;
	int mx = 0, id = 0;
	for(int i = 0; i < l; i++)
	
		p[i] = mx > i ? min(p[2 * id - i], 1ll * mx - i) : 1;
		while(ma[i + p[i]] == ma[i - p[i]] and check(ma[i + p[i]]) and check(ma[i - p[i]]))
			p[i] ++;
		if(i + p[i] > mx)
		
			mx = i + p[i];
			id = i;
		
	

void solve()

	int n;
	cin >> n >> (s + 1);

	int len = strlen(s + 1);
	manacher(s, len);

	ll res = 0;
	for(int i = 1; i < 2 * n + 2; i++)
	
		if(!check(ma[i])) continue;
		if(i & 1)
			res = (res + (p[i] - 1) / 2) % mod;
		else
			res = (res + p[i] / 2) % mod;
	
	cout << res << "\\n";


int main()

	ios::sync_with_stdio(false);
	cin.tie(0);
	int t;
	t = 1;
	// cin >> t;
	while(t--)
		solve();
	return 0;