常用算法公式之取模
Posted Huterox
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了常用算法公式之取模相关的知识,希望对你有一定的参考价值。
文章目录
前言
今天呢,我们先来简单地梳理一下咱们常用的一些数学公式,以及在咱们算法里面的运用。
例如咱们有时候求阶乘,求N项求和,那么这个时候,我们可以使用快速求法,或者直接使用数学公式例如无穷级数等,直接拿到结果。
求最大公约数(欧几里得算法)
怎么来的咱们不关心,咱们只需要知道m,n求公约数有这样的性质。
它们之间的公约数可以相互求余,值为0。
代码模板如下(这里给出java代码)
public static int gcd(int m,int n)
return n==0?m:gcd(n,m%n);
例如咱们比较经典的问题
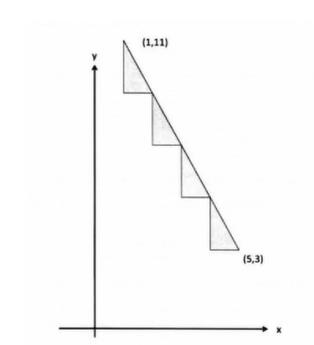
问这个直线段可以分几段。这个不就是求最大公约数的题目嘛,横坐标,纵坐标同时可以分为几份,这不就是变相求公约数嘛。(别问为什么不是最小的,问就是1)
贝祖等式
说到这个,咱们先来说说这玩意是干啥的。
一个方程组 ax+by = d
求x,y的解。并且d 是 a b的最大公约数。显然x,y有无穷多个解集。
首先我们这个是有规律的,我们只需要找到其中一个解就可以找到全部解。
就例如
12x + 42y = 6
4,-1是其中一个解。那么其他的解是啥
显然我们可以发现
4+(±)(42/6) , 1+(±)(12/6)
是另一组解,只要这样搞下去就是无穷个解。
那么问题时如何找到第一组解。
这里直接说递推公式
x = y1
y = x1 -a/b * y1
这个 x1,y1是第二步运算后的
public class 贝祖公式
static long x;
static long y;
static long gcd(long m,long n)
return n==0?m:gcd(n,m%n);
static long lcm(long a,long b)
//求最小公倍数
return a*b /gcd(a,b);
static long beizu(long a,long b)
if(b==0)
x = 1;
y = 0;
return a;
long res = beizu(b,a%b);
long x1 = x;
x = y;
y = x1-a/b*y;
return res;
static long linefunction(long a,long b,long m) throws Exception
long d = beizu(a,b);
if(m%d!=0) throw new Exception("无解");
long n = m/d;
x *=n;
y *=n;
return d;
class 贝祖test
public static void main(String[] args) throws Exception
贝祖公式.linefunction(12,42,6);
System.out.println("x:"+贝祖公式.x+" "+"y:"+ 贝祖公式.y);
这个拿到代码之后自己去调整,理解不了就死记,知道咋个用。
蓝桥杯:一步之遥
题目如下:
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
从昏迷中醒来,小明发现自己被关在 X 星球的废矿车里。 矿车停在平直的废弃的轨道上。 他的面前是两个按钮,分别写着 “F”“F” 和
“B”“B” 。小明突然记起来,这两个按钮可以控制矿车在轨道上前进和后退。 按 FF,会前进 9797 米。按 BB 会后退127127 米。
透过昏暗的灯光,小明看到自己前方 11 米远正好有个监控探头。 他必须设法使得矿车正好停在摄像头的下方,才有机会争取同伴的援助。
或许,通过多次操作 FF 和 BB 可以办到。矿车上的动力已经不太足,黄色的警示灯在默默闪烁… 每次进行 FF 或 BB 操作都会消耗一定的能量。
小明飞快地计算,至少要多少次操作,才能把矿车准确地停在前方 11 米远的地方。请问为了达成目标,最少需要操作的次数是多少。
这题目翻译出来就是 问
97x-127y=1的最小x+y的解
当然这题也是可以暴搜的
暴搜解法
这里我就直接写个python代码 了
x = 97
y = -127
ans = 100000#随便一个贼大的数
for i in range(300):
for j in range(300):
if i*x + j* y==1:
ans = min(ans, i+j)
print(ans)
贝祖解法(欧几里得)
这个就是直接用咱们的那个玩意求出的结果求和
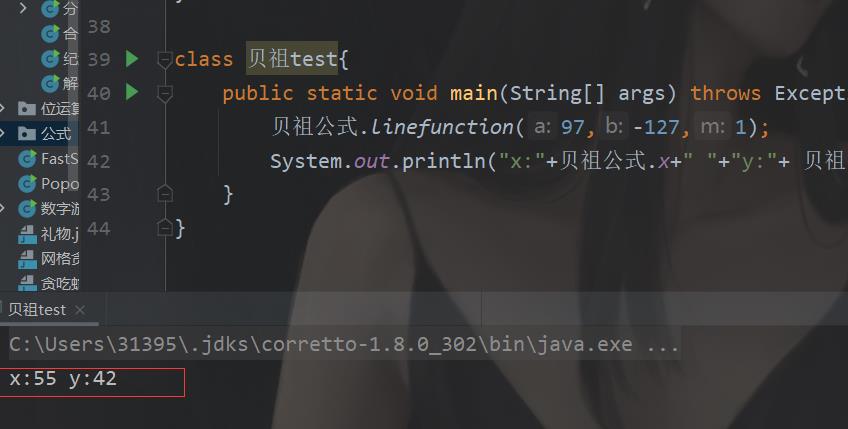
模运算(同余方程)
一说到模运算,他有两个非常神奇的功能。
1.运用模运算可以保留数的后几位
2.运用模运算可以实现不进位加法
举个爪子
例如 6666666333保留到后面的3个3如何做
直接 6666666333%1000 即可
不进位加法就更不用说了
9+8 % 10 = 7
此外本身还有个性质
5 % 3 = 2
5%2 == 3%2
这种规律。
当然咱们还有 快速取余这种性质
快速幂乘法&快速幂取余
不过这里还有一个性质
例如 5%3 %3 %3 你会发现
5%3 = 2
2% 3=2
如果一直 % 下去 效果可能是一样的,也就是说如果第一次的余数比去取模的数小,那么后面就没必要算了。
此外关于取模我们这样写
a % b = m
实际上对应
a = n*b + m
这样就意味着我们还可以使用这种方式去解方程。
此时在看道先前的性质
5%2 == 3%2
方程可以写成这样
a x + m y = b
x , y是一个整数。这样一来我把这玩意变成了一个方程。那么这个方程叫做同余方程。
目前为止,对于解方程,如果是 ax + by =1 的求解,我们可以使用那个贝祖定理。那么对于这个同余方程,我们还能这样处理。都说了是同余方程嘛。
当然问题是遇到这样的方程,带有求余数的方程,如何转化为线性方程。只要你会转,接下来你就是直接暴力,当然不转也能暴力,只是多知道一点嘛。
青蛙的约会(例题)
两只青蛙在网上相识了,它们聊得很开心,于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上,于是它们约定各自朝西跳,直到碰面为止。可是它们出发之前忘记了一件很重要的事情,既没有问清楚对方的特征,也没有约定见面的具体位置。不过青蛙们都是很乐观的,它们觉得只要一直朝着某个方向跳下去,总能碰到对方的。但是除非这两只青蛙在同一时间跳到同一点上,不然是永远都不可能碰面的。为了帮助这两只乐观的青蛙,你被要求写一个程序来判断这两只青蛙是否能够碰面,会在什么时候碰面。
我们把这两只青蛙分别叫做青蛙A和青蛙B,并且规定纬度线上东经0度处为原点,由东往西为正方向,单位长度1米,这样我们就得到了一条首尾相接的数轴。设青蛙A的出发点坐标是x,青蛙B的出发点坐标是y。青蛙A一次能跳m米,青蛙B一次能跳n米,两只青蛙跳一次所花费的时间相同。纬度线总长L米。现在要你求出它们跳了几次以后才会碰面。
Input
输入只包括一行5个整数x,y,m,n,L,其中x≠y < 2000000000,0 < m、n < 2000000000,0 < L < 2100000000。
Output
输出碰面所需要的跳跃次数,如果永远不可能碰面则输出一行"Impossible"
Sample Input
1 2 3 4 5
Sample Output
4
这里的话我们直接推方程是这样的
(x + km)%L = (y+kn)%L
然后我们展开
x + km = L* y1 + 余数
y + kn = L*y2 +余数
合并
(m-n)k + L(y1+y2) = y-x
y1+y2 变为一个未知数 t 因为他们表示的也就是时间嘛
(m-n)k + Lt = y-x
也就是这样的方程
ax + by = m
这样不就是回到了我们一开始的贝祖解法嘛
但是这里有个细节,那就是咱们对于负数的处理,这里咱们要点是x 但是x解出来可能是负数,显然我们要的是正数,那这个怎么处理咧。
这个直接套模板
我们的 那个是有返回值的那个方程里面
那么直接 b / 返回值 假设等于 c
那么 直接
x = (x%c + c) %c
下面是非暴力AC代码
自己改去
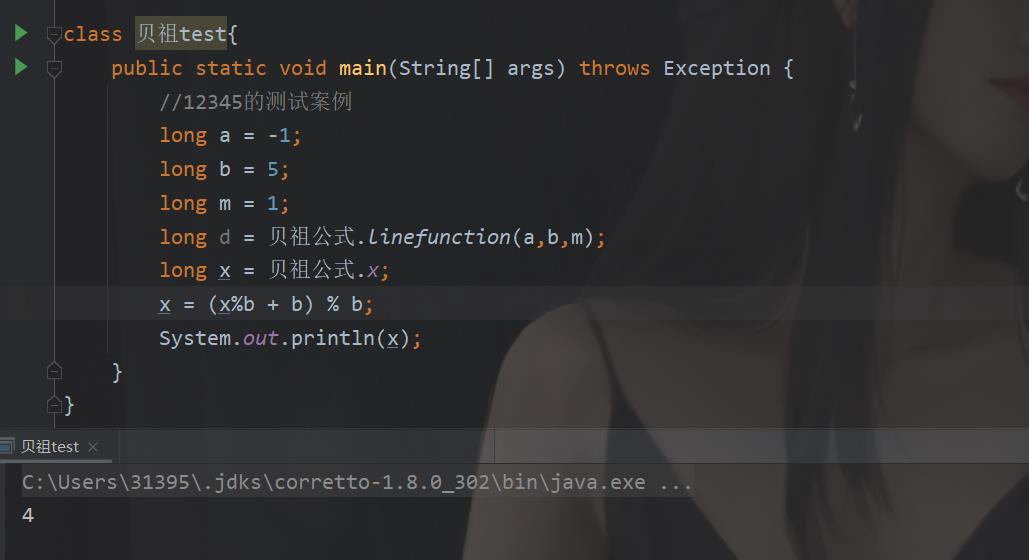
这个时候那可能要为我要 y 怎么办,我只能说数学是个好东西。
求逆元
这个怎么说呢,其实就是这个东西
a % b = m
a % m = b % m = 1
写出方程就是:
ax + by = 1
我看了人家的代码,其实和咱门那个代码是类似的直接用,只不过我们要注意x是负数的情况。
例如
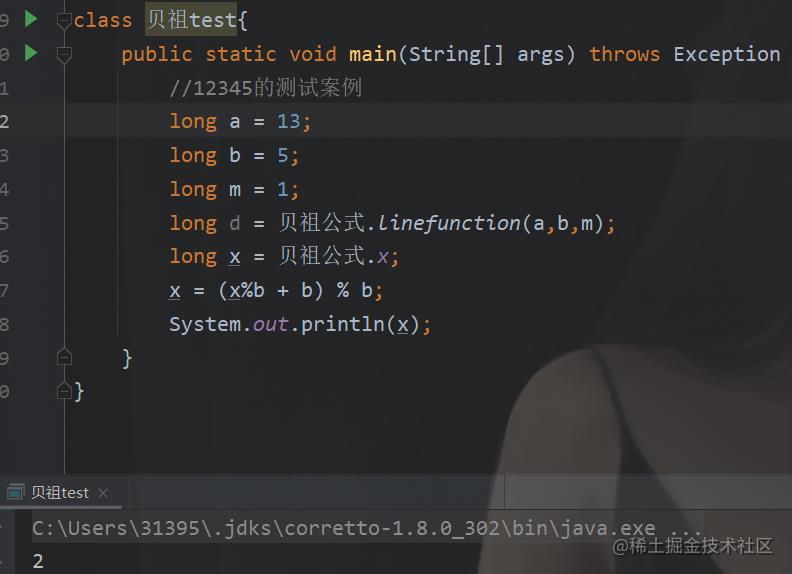
13x == (1%5)
也就是
13x % 5 == 1%5 求出咱们x的最小值(非负的)
总结
我们今天的重点就是这个那个线性方程,只要方程里面出现这种取模运算,这种线性的方程,我们就可以想办法去转换出来
以上是关于常用算法公式之取模的主要内容,如果未能解决你的问题,请参考以下文章