机器学习与scikit-learn-13]:算法 - 分类的本质与样本分布的离散程度的指标:纯度信息熵 基尼指数.
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习与scikit-learn-13]:算法 - 分类的本质与样本分布的离散程度的指标:纯度信息熵 基尼指数.相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:
目录
第2章 纯度(purity)的基本概念(以2个维度的向量为例)
第1章 分类问题的本质
1.1 多特征样本的本质
如果说,我们把每个样本的所有特征组成一个一维的向量 (X1, X2, X3......Xn),那么所有的样本就组成二维的矩阵。
每个样本,本质上就是(X1, X2, X3....Xn)维度空间中一个点,而所有样本就是分布在n维度空间中的所有点。
(1)n = 1时(1个特征:X1)
如果n=1,样本就是数轴上的一个个的点,最常见的对数轴上的点进行分类的方式如下所示:
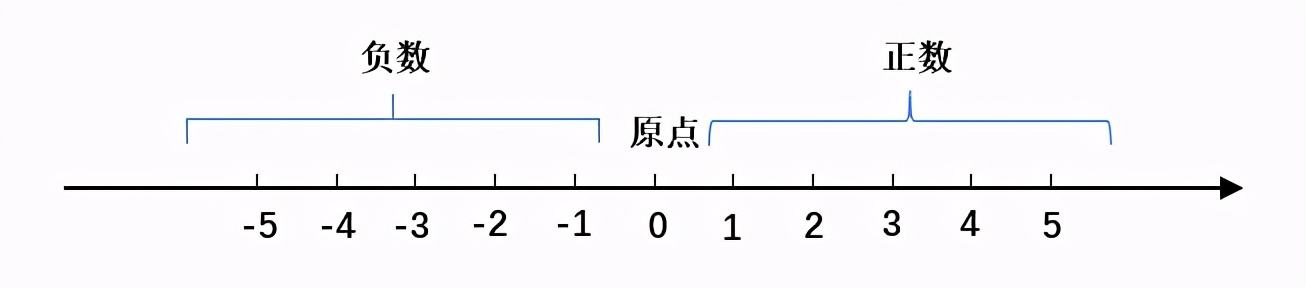
这里有三个分类:复数、原点、正数。大于0的划分为正数,小于0的数划分为正数,0划分为原点。
除了这种划分外,常见的就是把考试的分数划分为5个等级,所有落在区间内的点,都会被归为1-5的某个类。

每个样本就是数轴上的一个点(X1)
(2)n = 2时(2个特征: X1, X2)
当特征变成2是,样本就有数轴上的一个点,变成了平面上的一个点(X, Y)=> (X1, X2)
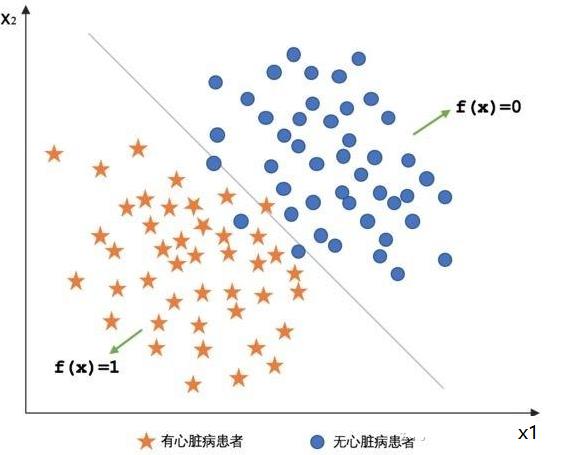
每个样本就是平面上的一个点(X1, X2)
(3)n = 3时(3个特征: X1, X2, X3)
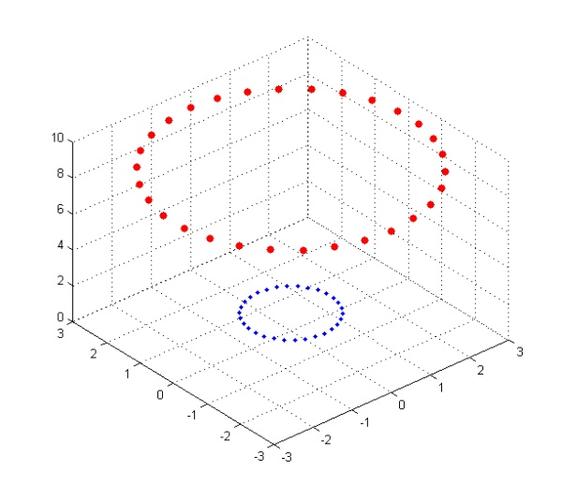
每个样本就是空间中的一个点(X1, X2, X3)。
(4)n>3时
每个样本就是n维度空间中的一个点(X1, X2, X3, X4.......)
1.2 分类的本质
分类的本质就只使用
(1)n=1

就是通过适当的函数y = f(X1), 能够把数轴上的点进行等级划分。
如:
X1 >=90且X1<100时, Y = 5
X1>=80且X1<90时, Y = 4
X1>=70且X1<80s时, Y = 3
X1>=60且X1<70时, Y = 2
X1>=50且X1<60时, Y = 1
(2)n=2
案例1:

在上图案例中,就是找到合适的函数F = (X1, X2), F= 0或1两种分类
案例2:
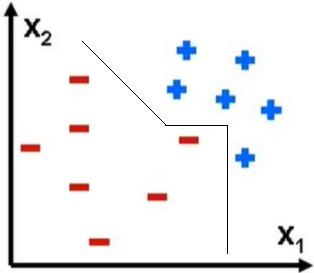
在上图中,就是找到三个函数F1(X1, X2) , F2(X1, X2), F3(X1,X2) 三个函数,联合完成对上述点的分类。
案例3:
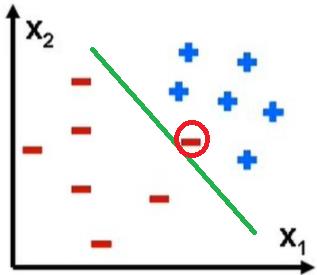
也可以仅仅通过一个函数F1(X1, X2)完成对上述的分类。
但这种简化的划分,有可能导致,部分的样本被错误的归类。如上图中被圈红的点。
(3)n=3

在上图案例中,就是找到合适的函数F = (X1, X2, X3), F= 0或1两种分类.
(4)n > = 3时
就是找到合适的函数F = (X1, X2, X3, X4....Xn), F= 0或1两种分类.
第2章 纯度(purity)的基本概念(以2个维度的向量为例)
2.1 纯度概述
如何表示某一种划分函数F(X1, X2)划分的好坏呢?
这里可以用纯度或准确率表示。
(1)情形1:上图,简单的通过象限划分,把所有的样本归为一个类
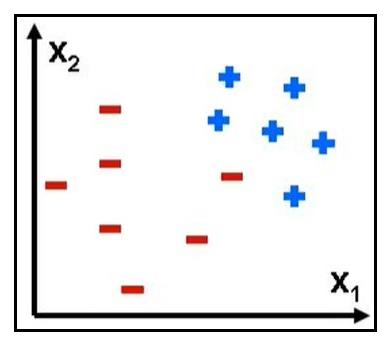
如果判决为红色,纯度为=7/15 = 54%, 准确率为54%
如果判决为蓝色,纯度为=6/15 = 46%,准确率为46%
(2)情形2:通过15个方框来划分
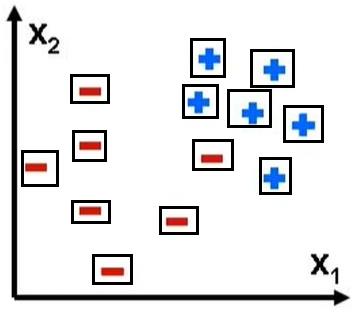
每个方框,代表一个判决函数Fm(X1, X2)
上图有13个判决节点,即13个判决规则,判决函数。
每个判决点的纯度 = 100%,精度100%正确。
但这种方法复杂,需要大量的函数F1(X1, X2), F2(X1, X2), F3(X1, X2)........
(3)情形3:折中方案,选中一个直线函数

通过一条直线判决函数F(X1, X2)进行判断
直线的左方判决/分类为红色,纯度为100%。
直线的右方判决/分类为蓝色,纯度为6/7=85%。
2.2 纯度与概率的关系
纯度的大小反应了确定性的大小。
(1)纯度趋于100%
纯度越高,确定性越大,为某一个分类的概率越大,不确定性就越小,信息量就越小。
纯度100%,表明是完全确定性事件,为某个分类类型的概率为100%,不确定性为0, 信息量为0.
(2)纯度趋于0%
纯度越小,为某一个分类的概率越小,为另一个分类的概率越大,不确定性同样越大越大,信息量就越小。
纯度0%,表明是完全确定性事件,为另一个分类类型的概率为100%,不确定性为0, 信息量为0.
(3)纯度为等分概率时
只有当纯度为所有样本的等分概率时,这时候,所有样本的纯度相等,表明不确定性最大,信息量最大。
某种数据类型的纯度 = 该分类在全部样本空间中出现的概率。
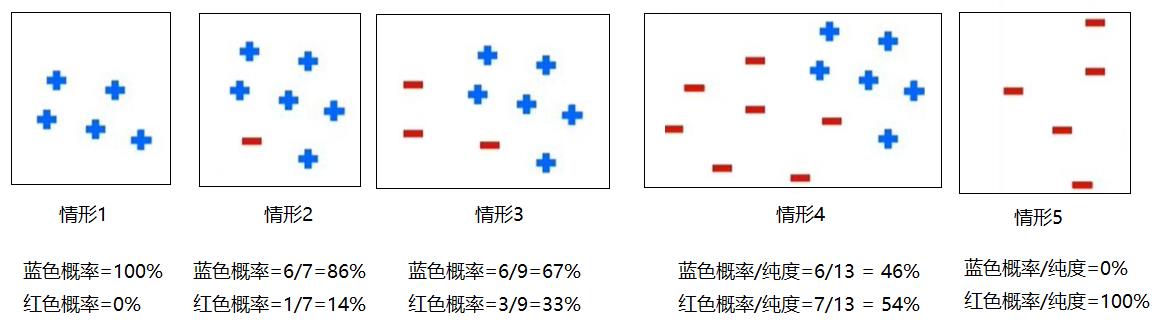
从上述的直观分析来看,情形1和5是最理想的分类,情形4是最不理想的分离。
如何使用数学的方式来表达上述分类的效果呢?
(1)用概率p的大小吗?
蓝色概率100%和0%的概率相差很大,但其实这时候效果都是最好的。
(2)用基尼系数表示:H(p) = p *(1-p)?
(3)用信息熵表示: H(p) = - p * log(p) ?
基尼系数和信息熵是最常用的用来表示样本空间中所有样本的发生的概率来描述样本样本的集中度或离散型的函数:
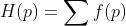
其中p不同样本的概率,
f表示基尼系数或信息熵函数,
y值的大小表示样本的离散分布程度,或者说随机性的大小。
下面我们就看看这两种函数与概率p的关系。
2.3 不纯度
1 - 纯度 = 不纯度
纯度越高,某个类别出现的概率值越大,则不确定性越小,信息量越小。
纯度越高,某个类别出现的概率值越效,则不确定性越大,信息量越大。
那么如何通过数学的方法取得一个折中,如何衡量或度量“纯度”呢?
由此引入基尼系数和“信息熵”的概念。
纯度 = 确定性 = 集中度 = 聚合度 =
不纯度 = 不确定性 = 熵值 = 随机性 = 离散型 = 信息量 = 混杂程度
第3章 基尼指数(Gini index)
3.1 基尼系数与p的关系:数学公式
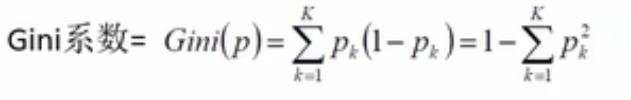
当某个事件或分类的概率为p时,用H(p) = p*(1-p) 表示该事件/分类的基尼系数。
所有事件/分类各自吉尼斯之和,就是总的基尼系数。
样本空间内,所有事件/分类的概率之和恒定为1。
那么把概率变换成基尼系数后的数值与样本空间中样本的分布概率是什么关系呢?
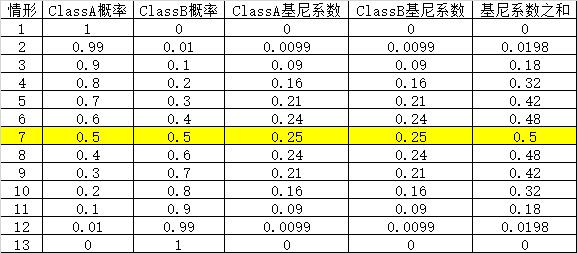
3.2 基尼系数与p的关系:表格表示(以两分类为例)
我们以二分类为例,来展现样本的概率与基尼系数之间的图形关系:
3.3 基尼系数与p的关系:图形表示(以两分类为例)
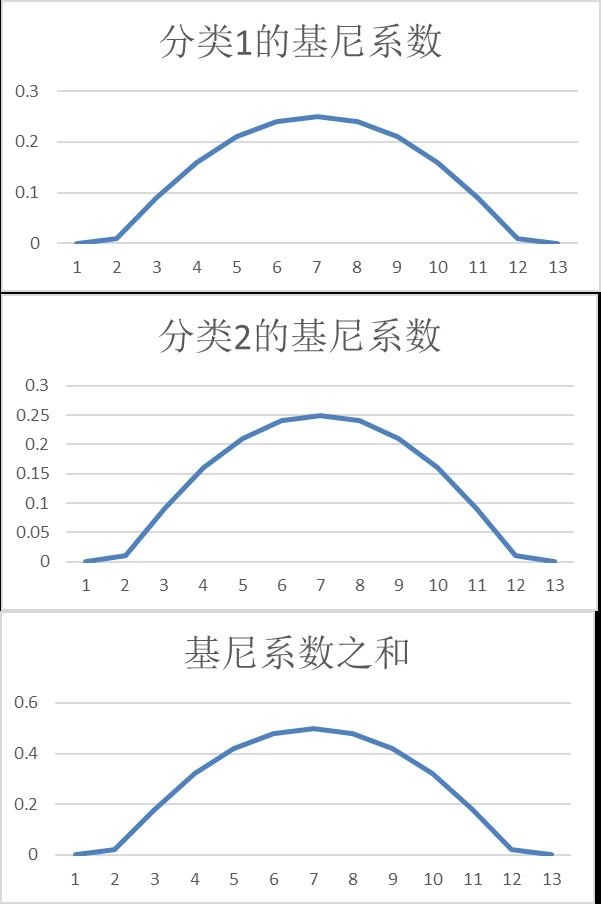
横轴是序号,对应的概率,可以查看上表。序号7时最大,对应的概率为0.5。
当样本概率为0.5时,表明两个样本是等概率分布的,最分散,没有任何侧重点,即随机分布程度越大,此时基尼系数为最大。
当样本概率为1和0时,表明样本空间中样本最集中,要么是ClassA,要么是ClassB, 这是确定性的,集中的。此时的基尼系数为0.
当各自的概率为1/2时,此时ClassA和ClassB的基尼系数都为0.25,达到最大值,基尼系数的和为0.5,也得到最大值。
因此,基尼系数通过样本空间个样本的概率分布情况,能够量化出样本空间中的分类样本的集中程度。
数值越小,集中程度越高,分散度越小。
数值越大,集中程度越小,分散度越大。
除了通过基尼系数能够根据空间个样本的概率分布情况,计算出样本的集中程度,有没有其他计算方法呢?
信息熵是另一种方法。
第4章 信息熵(information entropy)
4.1 信息熵与p的关系:数学公式
假定当前样本集合D中第k类样本所占的比例为pk(k=1,,2,...,|y|),则D的信息熵定义为:
Ent(D) = -∑k=1 pk·log2 pk (约定若p=0,则log2 p=0)
显然,Ent(D)值越小,D的纯度越高。因为0<=pk<= 1,故log2 pk<=0,Ent(D)>=0. 极限情况下,考虑D中样本同属于同一类,则此时的Ent(D)值为0(取到最小值)。当D中样本都分别属于不同类别时,Ent(D)取到最大值log2 |y|.
在一个样本集合中,信息熵反应了样本的离散程度、随机程度。
信息熵越大,离散程度越高,当所有样本都是等概率时,随机程度最大=1.
信息熵越小,离散程度越低,当只有某一个样本概率100%,其它样本概率为0%时,随机程度最小=0.
4.2 信息熵与p的关系:表格表示(以两分类为例)
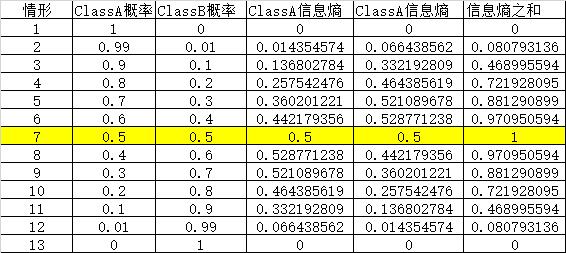
4.3 信息熵与p的关系:图形表示(以两分类为例)
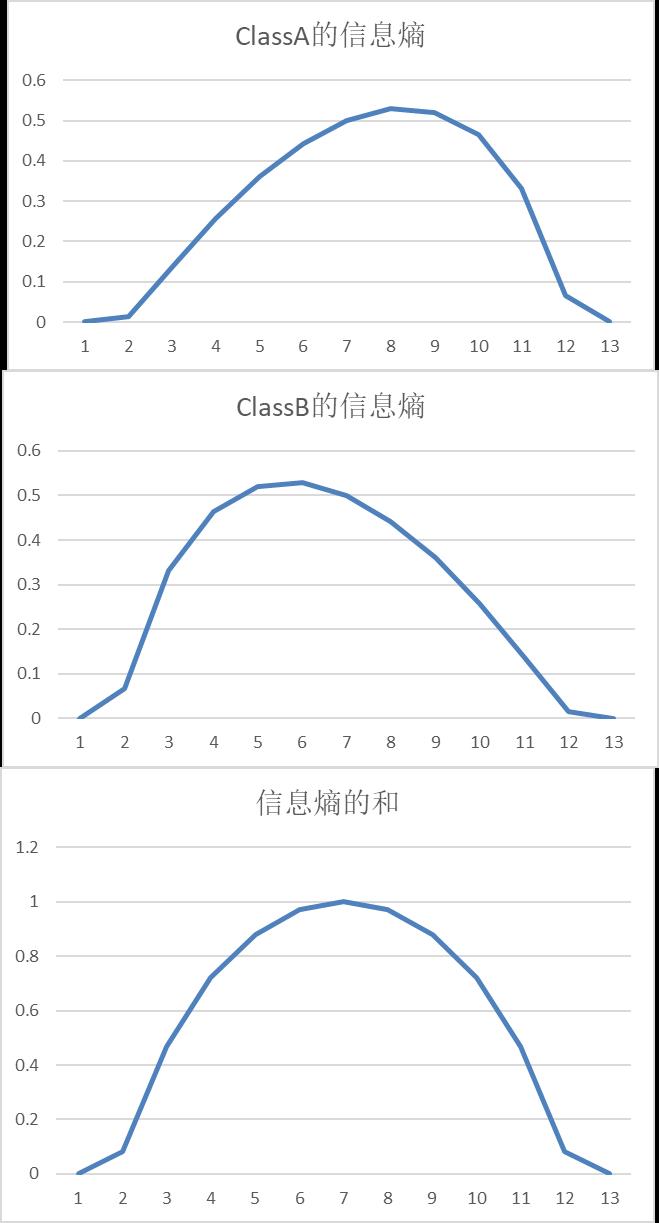
横轴是序号,对应的概率,可以查看上表,序号7时最大,对应的概率为0.5。
从上图的形状可以看出:
相同点:
(1)信息熵与基尼系数的图形的形状是非常相似的。
(2)它们都反应了样本空间中所有样本概率与信息熵的大小关系。
(3)当所有样本的概率相差越大,则表示集中度越高,离散度越小。
(4)当所有样本的概率相差越小,则表示集中度越小,离散度越大。
(5)当所有样本的概率为等概率时,每个样本的概率相差为0,则表示集中度最小,离散度最大,随机性最大,信息量最大, 为1。
(6)当其中一个样本的概率为100%,其他项目的概率则为0%, 则表示集中度最大,离散度最小,随机性最小,信息量最小,为0。
不同点:
(1)每个样本的离散性的累加和的最大值不同,基尼系数最大值为0.5, 信息熵最大值为1.
(2)单个样本的离散型的图形趋势不同:基尼系数是对称的,信息熵是不堆成的。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:
以上是关于机器学习与scikit-learn-13]:算法 - 分类的本质与样本分布的离散程度的指标:纯度信息熵 基尼指数.的主要内容,如果未能解决你的问题,请参考以下文章