二叉树需要掌握的基本知识

Posted 2022-03-02 TangguTae

目录

二叉树的特点：

特殊的二叉树

1、满二叉树

2、完全二叉树

二叉树的性质

二叉树的结构

1、顺序结构

 2、链式结构

二叉树的遍历

二叉树的四种遍历方式

四种遍历的代码实现

---

二叉树是树的一种特殊的结构

二叉树的特点：

1、每个节点最多两颗子树，即二叉树不存在度大于2的节点（每个节点最多两个子节点）。

2、二叉树的子树有左右之分，其子树的次序不能颠倒。

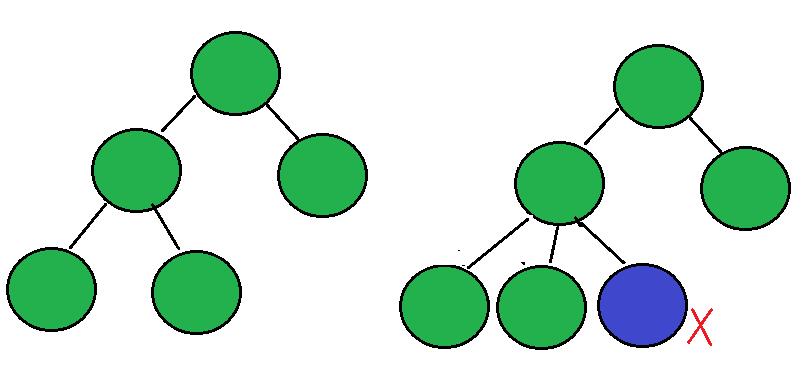
特殊的二叉树

1、满二叉树

每一层的节点数都达到最大值，或者是一个二叉树的深度为k，总的节点数为2^k -1。

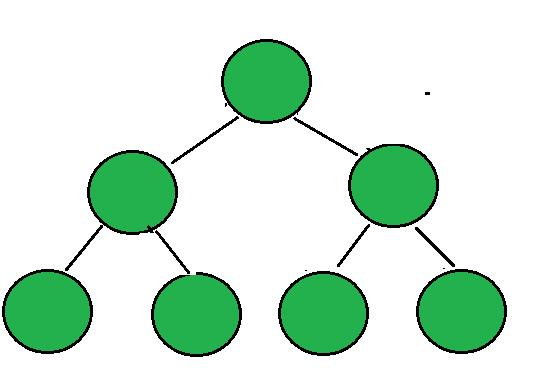
2、完全二叉树

深度为k的二叉树，前k-1层是满二叉树，最后一层可以不满，但是从左到右得是连续的。满二叉树是完全二叉树的一种特殊情况。

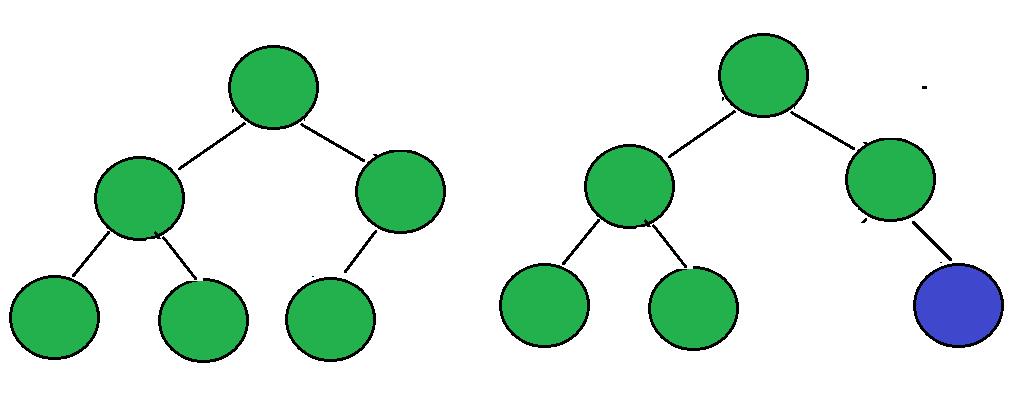
左边的就是完全二叉树，右边的是非完全二叉树。

---

二叉树的性质

1、若规定根节点的层数为1，则一棵非空二叉树的第 i 层上最多有2^(i-1)个节点。

2、若规定根节点的层数为1，则深度为 h 的二叉树的最大结点数是2^h- 1。

3、若规定根节点的层数为1，具有n个节点的满二叉树的深度为log以2为底，n+1为对数。

4、对于任何一棵二叉树，如果度为0的叶节点个数为n0，度为2的节点个数为n2，则n0=n2+1，也就是说度为0的比度为2的节点数多一个

例题：

1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ B ）
A 不存在这样的二叉树
B 200
C 198
D 199

解释：度为0的节点比度为2的节点多一个

2.下列数据结构中，不适合采用顺序存储结构的是（ A ）
A 非完全二叉树
B 堆
C 队列
D 栈

解释：顺序适合存储连续的结构，非完全二叉树结构不连续

3.在具有 2n 个结点的完全二叉树中，叶子结点个数为（ A ）
A n
B n+1
C n-1
D n/2

解释：假设度为0的节点有x个，则度为2的节点有x-1个。此时度为0的节点只有两种可能要不只有一个，要不一个都没有（因为是完全二叉树）。所以我们可以得到x+x-1+1=2n或者x+x-1=2n两种情况的方程。由于节点只能为整数，所以x只能为n；

4.一棵完全二叉树的节点数位为531个，那么这棵树的高度为（ B ）
A 11
B 10
C 8
D 12

解释：假二叉树的高度为9，则满二叉树的节点个数为2^9 - 1 = 511 < 531。所以该二叉树的高度肯定比9高，高度为10的二叉树节点个数为2^10 - 1 = 1023个 > 531。所以高度只能为10

5.一个具有767个节点的完全二叉树，其叶子节点个数为（ B ）
A 383
B 384
C 385
D 386

解释：和第三题相似，分情况讨论，利用n0 = n2 + 1关系来计算。

---

二叉树的结构

1、顺序结构

普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。

 

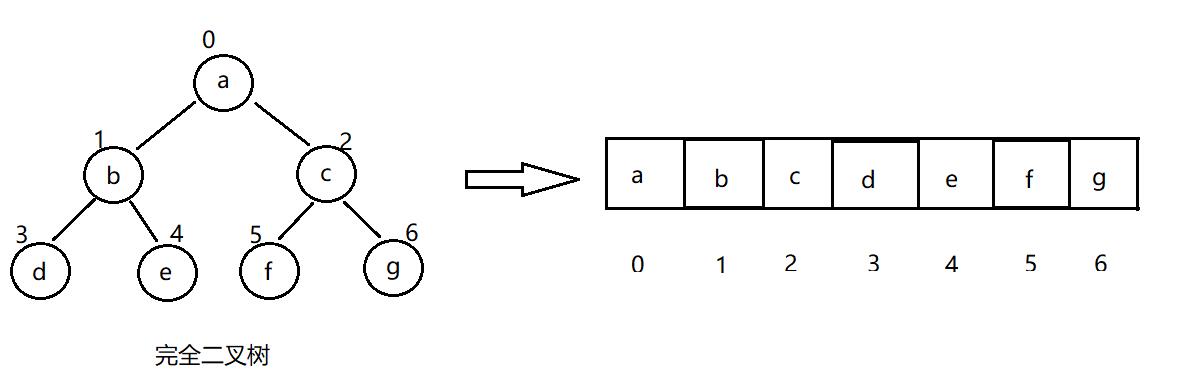
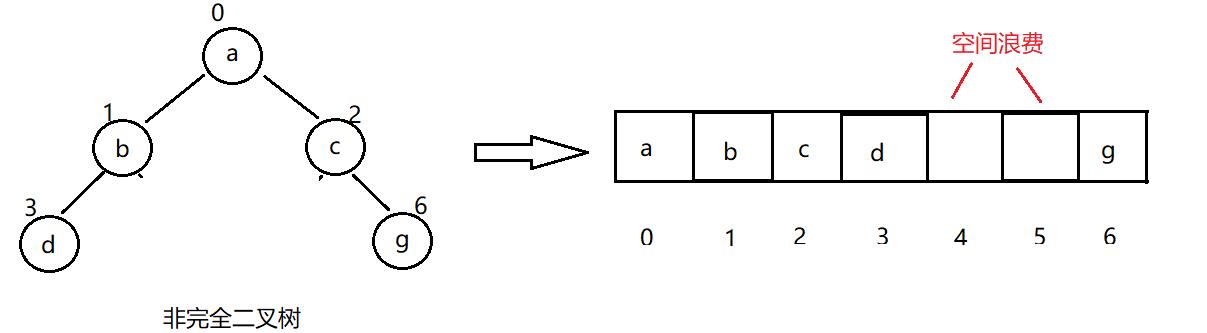
 这种结构一般用在堆上。注意这里的堆是一种数据结构，而不是操作系统层面上的堆区。

 2、链式结构

数组只适合用来表达完全二叉树，如果不是完全二叉树，只能采用链表。

(1) 二叉链

采用结构体来实现这种结构。

typedef char BTDataType;

typedef struct BinaryTreeNode

	struct BinaryTreeNode* left;//指向左孩子节点
	struct BinaryTreeNode* right;//指向右孩子节点
	BTDataType data;//自身节点的数据

BTNode;

(2) 三叉链

三叉链在二叉链的基础上多增加了一个指向父亲节点的指针。

typedef char BTDataType;

typedef struct BinaryTreeNode

	struct BinaryTreeNode* left;//指向左孩子节点
	struct BinaryTreeNode* right;//指向右孩子节点
	struct BinaryTreeNode* parent;//指向父亲节点
	BTDataType data;//自身节点的数据

BTNode;

---

二叉树的遍历

二叉树的四种遍历方式

 

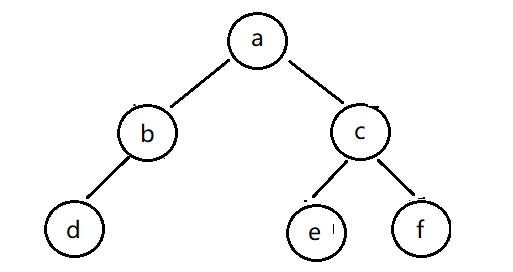
1、前序遍历（先根遍历）：根->左子树->右子树

参考上图的二叉树，得到的结果为：abdcef

2、中序遍历（中根遍历）：左子树->根->右子树

得到的结果为：dbaecf

3、后序遍历（后根遍历）：左子树->右子树->根

得到的结果为：dbefca

4、层序遍历：从左往右一层层的遍历

得到的结果为：abcdef

四种遍历的代码实现

采用二叉链的方式构建一棵树

1、前序遍历

采用递归的思想：按照前序遍历的顺序（根->左子树->右子树），递归的方法本身很简单，非递归的方法值得一做。

LeetCode链接：144. 二叉树的前序遍历 - 力扣（LeetCode） (leetcode-cn.com)

class Solution 
public:
    void _preorderTraversal(TreeNode* root, vector<int>& v) 
        if(root == nullptr)
            return;
        v.push_back(root->val);//先记录根节点
        _preorderTraversal(root->left, v);//然后在遍历左子树
        _preorderTraversal(root->right, v);//左子树遍历完了以后遍历右子树
    
    vector<int> preorderTraversal(TreeNode* root) 
        vector<int> v;
        _preorderTraversal(root,v);
        return v;
    
;

2、中序遍历

采用递归的思想：按照中序遍历的顺序（左子树->根->右子树）

LeetCode链接：94. 二叉树的中序遍历 - 力扣（LeetCode） (leetcode-cn.com)

class Solution 
public:
    void _inorderTraversal(TreeNode* root,vector<int>& v)
    
        if(root == nullptr)
            return;
        _inorderTraversal(root->left,v);//先遍历左子树
        v.push_back(root->val);//记录节点
        _inorderTraversal(root->right,v);//在遍历右子树
    
    vector<int> inorderTraversal(TreeNode* root) 
        vector<int> v;
        _inorderTraversal(root,v);
        return v;
    
;

3、后序遍历

采用递归的思想：按照后序遍历的顺序（左子树->右子树->根）（这个的非递归有一定的难度）

LeetCode链接：145. 二叉树的后序遍历 - 力扣（LeetCode） (leetcode-cn.com)

class Solution 
public:
    void _postorderTraversal(TreeNode* root, vector<int>& v) 
        if(root == nullptr)
            return;
        _postorderTraversal(root->left, v);//左
        _postorderTraversal(root->right, v);//右
        v.push_back(root->val);//根
    
    vector<int> postorderTraversal(TreeNode* root) 
        vector<int> v;
        _postorderTraversal(root,v);
        return v;
    
;

4、层序遍历

层序遍历比上述三种遍历稍微复杂一点

思想：采用迭代的方法，需要利用数据结构队列来辅助遍历，每次将根节点入队列时，需要把根节点的左子树的根节点和右子树的根节点依次入队列。

class Solution 
public:
    vector<vector<int>> levelOrder(TreeNode* root) 
        vector<vector<int>> vv;
        queue<TreeNode*> q;//存放节点的地址
        if(root != nullptr)
            q.push(root);
        while(!q.empty())
        
            int size = q.size();//判断每一层有多少个节点
            vector<int> v;//存放每一层的节点值
            while(size)
            
                if(q.front()->left)//左子树存在
                    q.push(q.front()->left);
                if(q.front()->right)//右子树存在
                    q.push(q.front()->right);
                v.push_back(q.front()->val);
                q.pop();
                size--;
            
            vv.push_back(v);
        
        return vv;
    
;