5. 最长回文子串（动归/中心扩展法）

Posted 2022-02-27 Ston.V

1.Description

给你一个字符串 s，找到 s 中最长的回文子串。

2.Example

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。
示例 2：

输入：s = "cbbd"
输出："bb"

3.My code(Not AC,timeout)

暴力求解

class Solution 
public:

    bool isCircle(string s)
        for(int i=0;i<s.length()/2;i++)
            if(s[i]!=s[s.length()-1-i])
                return false;
        
        return true;
    

    string longestPalindrome(string s) 
        int len =0;
        string res="";
        for(int i=0;i<s.length();i++)
            for(int j=1;j<=s.length()-i;j++)
                string tmp = s.substr(i,j);
                if(isCircle(tmp) && tmp.length()>len)
                    len = tmp.length();
                    res = tmp;
                
            
        
        return res;
    
;

4.Code（动态规划）

动态规划，状态转移方程为（如果[i,j]是回文串，那么只有s[i-1]==s[j+1]时，[i-1,j+1]才也是回文串）：

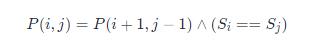
初始条件为（当长度为1和2时，直接判断）：

 

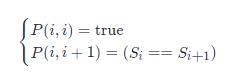
 错误写法：直接遍历i,j无法得到正确结果！！！！！！

比如当你求dp[0][3]时，你连dp[1][2]都没有开始求，因此无法递推到正确结果；需要使用步长来循环，然后才能开始递推。你得懂你递推的是什么啊！！！

class Solution 
public:

    string longestPalindrome(string s) 
        int n = s.length();
        //动归矩阵
        vector<vector<bool>> dp(n,vector<bool>(n));
        if(n<2)
            return s;
        
        //初始化
        for(int i=0;i<n;i++)
            dp[i][i]= true;
        
        int len=1;
        string res=s.substr(0,1);
            
        //遍历二维数组
        for(int i=0;i<n;i++)
            for(int j=i+1;j<n;j++)
                if(s[i] != s[j])
                    dp[i][j]=false;
                else
                    if(j-i+1<=2)
                        dp[i][j]=true;
                    else
                        dp[i][j]=dp[i+1][j-1];
                
                if(dp[i][j] && j-i+1>len)
                    len = j-i+1;
                    res = s.substr(i,j-i+1);
                
            
        return res;      
    
;

正确code:需要使用步长来递推

class Solution 
public:

    string longestPalindrome(string s) 
        int n = s.length();
        //动归矩阵
        vector<vector<bool>> dp(n,vector<bool>(n));
        if(n<2)
            return s;
        
        //初始化
        for(int i=0;i<n;i++)
            dp[i][i]= true;
        
        int len=1;
        string res=s.substr(0,1);
            
        //依步长递推
        for(int step=1;step<=n;step++)
            for(int i=0;i<n;i++)
                int j = i+step-1;
                if(j>=n)
                    break;
                if(s[i]==s[j])
                    if(step<=2)
                        dp[i][j]=true;
                    else
                        dp[i][j]=dp[i+1][j-1];
                else
                    dp[i][j]=false;

                if(dp[i][j] && step>len)
                    len = step;
                    res = s.substr(i,step);
                
            
        
        return res;      
    
;

5.思路

1.动归你得看看你这是靠什么在递推，这里直接双层for i，j是递推不出来的

2.注意这里的边界是串长为1或2，在递推中判断长为2的情况

3.中心扩展法（容易理解）：

我们枚举所有的「回文中心」并尝试「扩展」，直到无法扩展为止，此时的回文串长度即为此「回文中心」下的最长回文串长度。我们对所有的长度求出最大值，即可得到最终的答案。

class Solution 
public:
    pair<int, int> expandAroundCenter(const string& s, int left, int right) 
        while (left >= 0 && right < s.size() && s[left] == s[right]) 
            --left;
            ++right;
        
        return left + 1, right - 1;
    

    string longestPalindrome(string s) 
        int start = 0, end = 0;
        for (int i = 0; i < s.size(); ++i) 
            auto [left1, right1] = expandAroundCenter(s, i, i);
            auto [left2, right2] = expandAroundCenter(s, i, i + 1);
            if (right1 - left1 > end - start) 
                start = left1;
                end = right1;
            
            if (right2 - left2 > end - start) 
                start = left2;
                end = right2;
            
        
        return s.substr(start, end - start + 1);
    
;