备战面试算法每日一练
Posted 温文艾尔
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了备战面试算法每日一练相关的知识,希望对你有一定的参考价值。
⭐️写在前面
文章目录
⭐️1.合并二叉树
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始
来源:力扣(LeetCode)617
链接:点击跳转
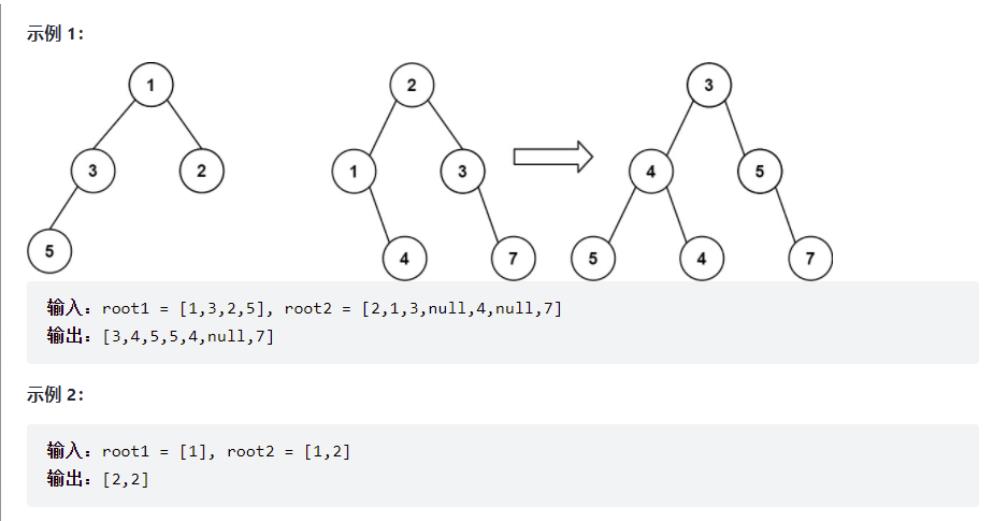
我们修改原来树的结构,重复利用root1这棵树,root1就是合并之后树的根节点,具体我们采用前序遍历和迭代
前序遍历法
package day10;
/**合并二叉树
* Description
* User:
* Date:
* Time:
*/
class TreeNode
int val;
TreeNode left;
TreeNode right;
TreeNode()
TreeNode(int val) this.val = val;
TreeNode(int val, TreeNode left, TreeNode right)
this.val = val;
this.left = left;
this.right = right;
class Test01
public TreeNode mergeTrees(TreeNode root1, TreeNode root2)
if (root1==null) return root2;
if (root2==null) return root1;
root1.val+=root2.val;
root1.left = mergeTrees(root1.left,root2.left);
root1.right = mergeTrees(root1.right,root2.right);
return root1;
迭代法
//迭代
public TreeNode mergeTrees2(TreeNode root1, TreeNode root2)
if (root1==null) return root2;
if (root2==null) return root1;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root1);
queue.offer(root2);
while (!queue.isEmpty())
TreeNode root1Node = queue.poll();
TreeNode root2Node = queue.poll();
root1Node.val+=root2Node.val;
if (root1Node.left!=null&&root2Node.left!=null)
queue.offer(root1Node.left);
queue.offer(root2Node.left);
if (root1Node.right!=null&&root2Node.right!=null)
queue.offer(root1Node.right);
queue.offer(root2Node.right);
//存在其中一边为空的情况
if (root1Node.left==null&&root2Node.left!=null)
root1Node.left = root2Node.left;
if (root1Node.right==null&&root2Node.right!=null)
root1Node.right = root2Node.right;
return root1;
⭐️2.二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
来源:力扣(LeetCode)700
链接:点击跳转

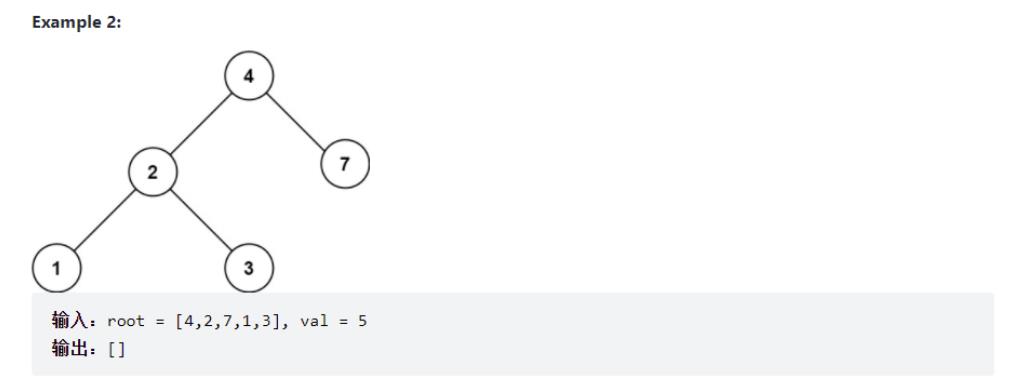
递归解决
public TreeNode searchBST(TreeNode root, int val)
if (root==null||root.val==val) return root;
if (root.val<val) return searchBST(root.right, val);
if (root.val>val) return searchBST(root.left, val);
return null;
迭代法1
public static TreeNode searchBST2(TreeNode root, int val)
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty())
TreeNode node = queue.poll();
if (node.val==val) return node;
if (node.left!=null) queue.offer(node.left);
if (node.right!=null) queue.offer(node.right);
return null;
迭代法2
public TreeNode searchBST3(TreeNode root, int val)
while (root!=null)
if (root.val>val) root = root.left;
else if (root.val<val) root = root.right;
else return root;
return null;
⭐️3.验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
来源:力扣(LeetCode)98
链接:点击跳转
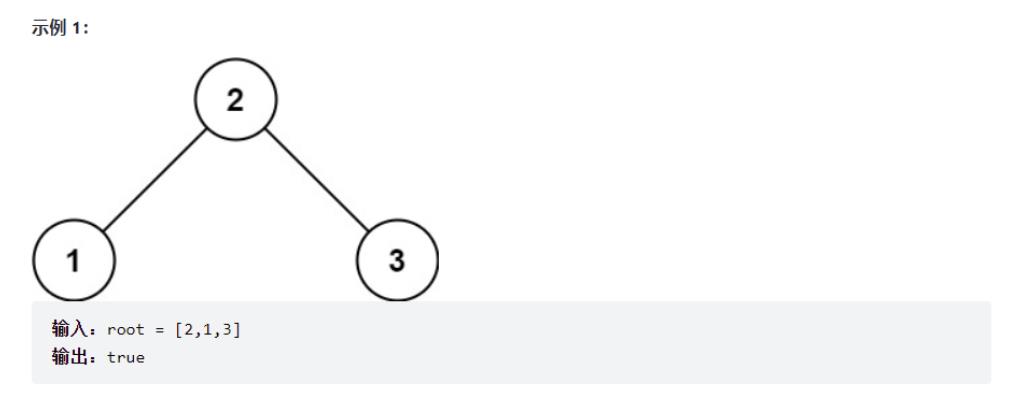
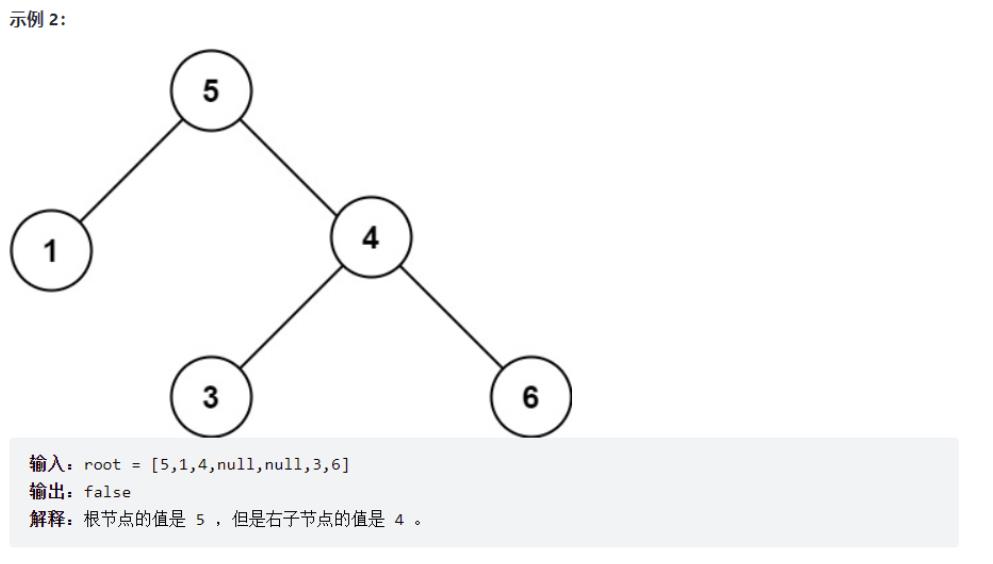
递归解决
public long pre = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root)
if (root==null)
return true;
if (!isValidBST(root.left))
return false;
if (root.val<=pre)
return false;
pre=root.val;
return isValidBST(root.right);
⭐️4.二叉搜索树的最小绝对差
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值。
差值是一个正数,其数值等于两值之差的绝对值。
来源:力扣(LeetCode)530
链接:点击跳转
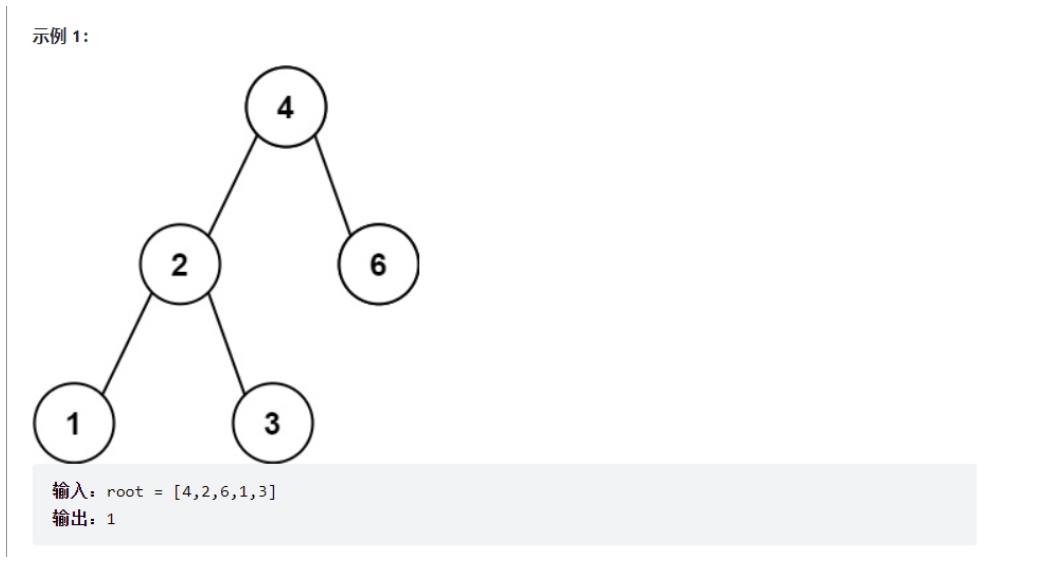
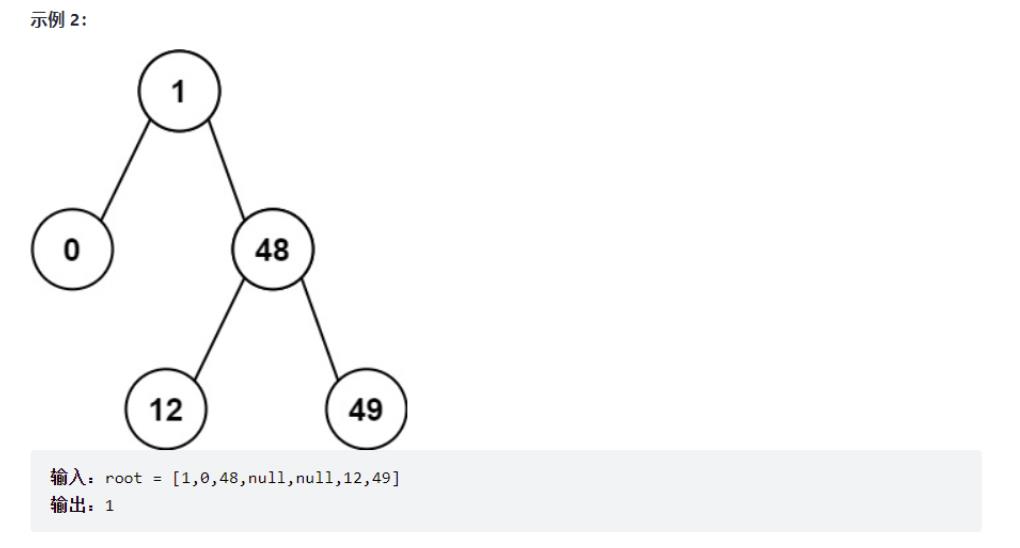
递归
int result = Integer.MAX_VALUE;//记录最小绝对值
TreeNode node = null;//记录上一个节点
public int getMinimumDifference(TreeNode root)
if (root==null)return 0;
defineResult(root);
return result;
public void defineResult(TreeNode root)
if (root==null) return;
defineResult(root.left);
result = Math.min(result,root.val-node.val);
node = root;
defineResult(root.right);
⭐️5.二叉搜索树中的众数
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树
来源:力扣(LeetCode)501
链接:点击跳转
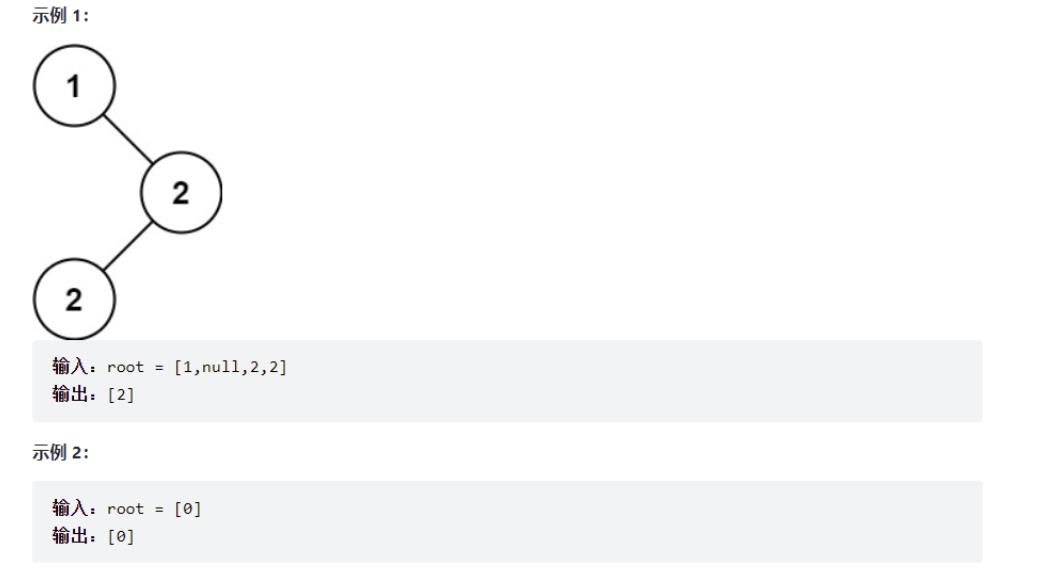
思路:利用map集合存储每个节点值出现的次数,次数最多的是众数
方法1:暴力破解
public static int[] findMode(TreeNode root)
Map<Integer,Integer> map = new HashMap<>();
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty())
TreeNode top = queue.poll();
map.put(top.val,map.getOrDefault(top.val,0)+1);
if (top.left!=null) queue.offer(top.left);
if (top.right!=null) queue.offer(top.right);
Set<Integer> keys = map.keySet();
List<Integer> list = new ArrayList<>();
int min = Integer.MIN_VALUE;
for (Integer key : keys)
if (map.get(key)>min)
list.clear();
min = map.get(key);
list.add(key);
continue;
if (map.get(key)==min)
list.add(key);
return list.stream().mapToInt(Integer::intValue).toArray();
方法2:中序遍历
public static List<Integer> list;
public static int count;
public static int maxCount;
public static TreeNode pre;
public static int[] findMode2(TreeNode root)
if (root==null) return new int[0];
list = new ArrayList<>();
pre = null;
count=0;
maxCount=0;
findDef(root);
int[] arr = new int[list.size()];
for (int i = 0; i < list.size(); i++)
arr[i] = list.get(i);
return arr;
private static void findDef(TreeNode root)
if (root==null) return;
findDef(root.left);
if (pre!=null&&pre.val==root.val)
count++;
else
count=1;
if (count==maxCount)
list.add(root.val);
else if (count>maxCount)
list.clear();
list.add(root.val);
maxCount = count;
pre = root;
findDef(root.right);
⭐️6.二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
来源:力扣(LeetCode)236
链接:点击跳转

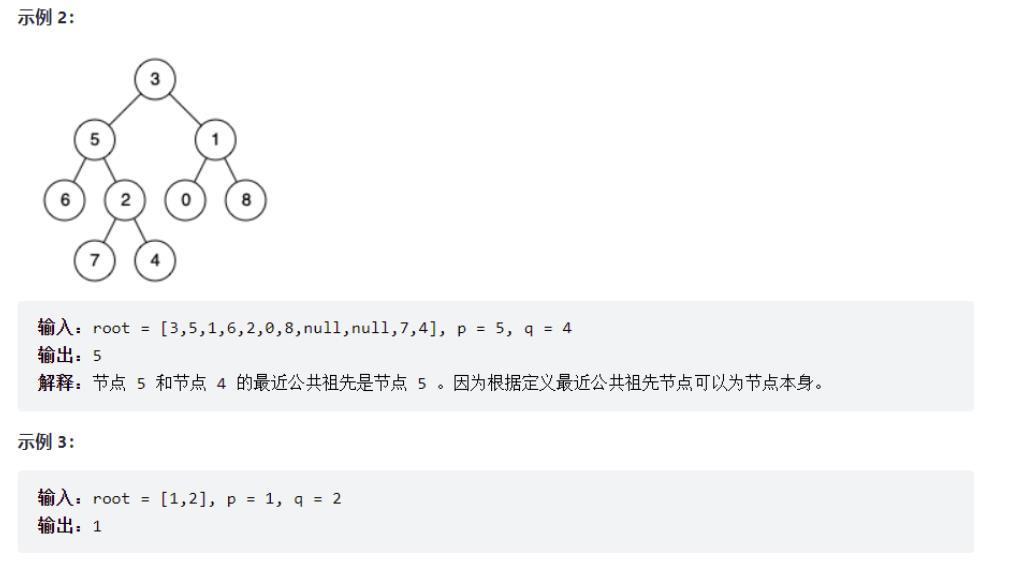
后序遍历
我们分别利用后序遍历从最底层开始寻找pq,进行回溯,有以下几种情况
- 左子树有q,右子树有p,左子树有p,右子树有q
- 左子树有pq,右子树无
- 左子树无,右子树有pq
- 左右子树均无
//采用后序遍历(左右根)
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q)
if (root==p||root==q||root==null) return root;
TreeNode treeNodeLeft = lowestCommonAncestor(root.left, p, q);
TreeNode treeNodeRight = lowestCommonAncestor(root.right,p,q);
if (treeNodeLeft!=null&&treeNodeRight==null)
return root;
if (treeNodeLeft!=null&&treeNodeRight==null)
return treeNodeLeft;
else if (treeNodeLeft==null&&treeNodeRight!=null)
return treeNodeRight;
else
return null;
以上是关于备战面试算法每日一练的主要内容,如果未能解决你的问题,请参考以下文章