数据结构和算法图必学的两种存储方式,看完即懂
Posted Linux猿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构和算法图必学的两种存储方式,看完即懂相关的知识,希望对你有一定的参考价值。
🎈 作者:Linux猿
🎈 简介:CSDN博客专家🏆,华为云享专家🏆,Linux、C/C++、云计算、物联网、面试、刷题、算法尽管咨询我,关注我,有问题私聊!
🎈 关注专栏: 数据结构和算法成神路【精讲】优质好文持续更新中……🚀🚀🚀
🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬

目录
上一篇文章对『 图的相关概念 』『图的相关概念』进行了详细的介绍,本文将对「图」的两种主要存储方式进行说明,分别是「邻接矩阵」存储和「邻接表」存储。
🍓一、图的存储方式
「图」的存储方式有许多中,包括〔邻接矩阵〕、〔邻接表〕、〔十字链表〕、〔邻接多重表〕等,但是,要说在「算法」中最长使用的只有两种:「邻接矩阵」和「邻接表」。它们两个各有优势,下面就来分别讲解下。
🔶🔶🔶🔶🔶 我是华丽的分割线 🔶🔶🔶🔶🔶
🍓二、邻接矩阵
🍅2.1 存储图
「邻接矩阵」存储是指通过二维的数组存储图,一般通过数组的横纵「下标」标识图的「顶点」,二维数组内存储的「值」标识图的「边」的状态,下面直接来看一个例子。
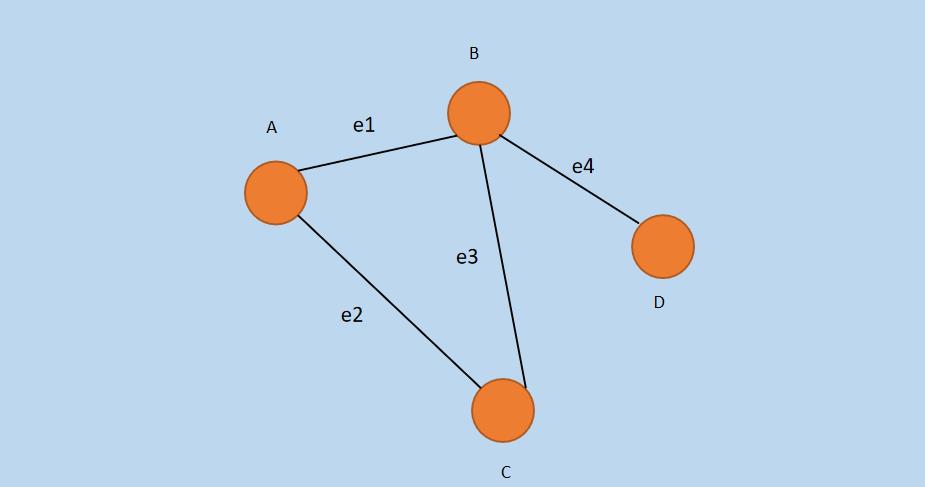
上述的无向图可以用如下的「二维矩阵」表示。
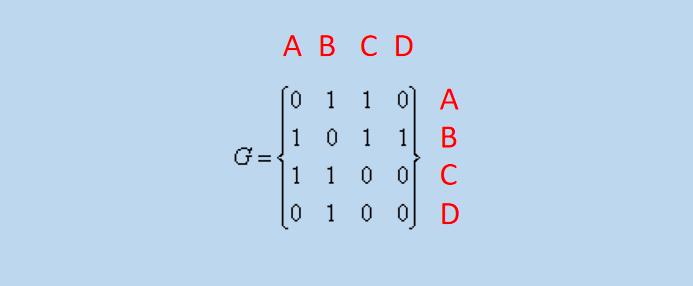
在上图的表示中,矩阵 G 表示二维数组。
其中,二维数组中的数字表示对应顶点之间的连接状态。
0 : 表示顶点之间没有边直接连接;
1 : 表示顶点之间存在直接连接;
例如:第一行第二列的 1 表示〔顶点 A〕 和 〔顶点 B〕 存在边直接连接,这条边就是「图 1」中的 〔 e1 〕,因为「图 1」是无向图,那么〔顶点 B〕 和〔顶点 A〕也是直接相连的,即:「图 2」中的第二行第一列的 1,第四行第1列的 0 表示顶点 A 和顶点 D 不存在边直接相连。
这样,就可以将「图 1」中的图存储到二维矩阵 G 中啦,存储后如「图 2」矩阵G所示。
好了,现在知道如何使用二维矩阵来存储「图」了,那么如何使用这个矩阵来遍历「图」呢 ?
🍅2.2 遍历图
谈到遍历「图」,最最最基本的操作便是如何判断〔顶点 V〕和〔顶点 W〕 是否存直接相连的边。正好,通过上面学习的「二维矩阵」,我们可以用 O(1) 的时间复杂度查询出「图」中任意两个顶点是否存直接相连的边。
例如:假设使用矩阵 G 存储「图」,判断从〔顶点 V〕到〔顶点 W〕 是否存在直接相连的边,那么只需要判断 G[i][j] (假设顶点 V 对应二维数组 G 的下标 i,W 对应下标 j)的值是否为 1 即可。
下面通过一个真实的例子来演示下。
假设使用「图 2」中的「二维矩阵」存储的「图 1」,判断 〔顶点 A〕 和 〔顶点 B〕 是否存在直接相连的边,只需要判断 G[0][1] 是否为 1 即可(「图 2」二维矩阵中〔顶点 A〕 对应下标 0,〔顶点 B〕对应下标 1)。
现在我们知道「图」基本的遍历操作了,那么,如何判断 「图」中某一〔顶点 P〕 到 〔顶点 Q〕的是否存在通路呢 ?
下面还是通过一个真实的例子来演示下。
假设使用「图 2」中的「二维矩阵」存储的「图 1」,判断从〔顶点 A〕和 〔顶点 D〕 是否存在一条路径。
代码实现如下所示:
#include <iostream>
using namespace std;
int n = 4; // 顶点数量
int G[4][4] = // 二维矩阵 G 存储的图
0, 1, 1, 0,
1, 0, 1, 1,
1, 1, 0, 0,
0, 1, 0, 0
;
bool dfsMatrix(int v, int w, int g[][4])
// 结束条件,遍历到顶点 w
if(v == w)
return true;
// 依次遍历与顶点 v 直接相连的边
for(int i = 0; i < n; ++i)
if(g[v][i])
g[v][i] = 0; // 标记访问过了
if(dfsMatrix(i, w, G))
return true;
g[i][v] = 1; // 恢复标记
return false;
int main()
//判断 A 和 D 是否存在路径
cout<<dfsMatrix(0, 3, G)<<endl;
return 0;
在上述代码中,二维数组 G 是「图 1」的矩阵存储,〔顶点 A〕对应二维矩阵下标 0,〔顶点 D〕 对应二维矩阵下标 1,所以 dfsMatrix(0, 3, G),上述遍历采用的算法是「深度优先搜索」的方式,使用矩阵 G 遍历图。
🔶🔶🔶🔶🔶 我是华丽的分割线 🔶🔶🔶🔶🔶
🍓三、邻接表
🍅3.1 存储图
「邻接表」主要通过存储图的边来存储一个图,从任意一个顶点出发,可以找到与其直接相连的边,不直接相连的边不存储在一起,下面通过一个例子来看一下。

使用「邻接表」存储「图 3」中的无向图,代码如下所示:
#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <algorithm>
using namespace std ;
const int MX = 1000;
int top;
int V[MX];
struct Edge
int v, w;
int next; //下标和内容均为边序号
E[MX];
// 初始化
void init()
top = 0;
memset(V, -1, sizeof(V));
// 存储无向图
void addAdge(int u, int v, int w)
// 将边 <u, v> 与顶点 u 关联
E[top].v = v;
E[top].w = w;
E[top].next = V[u];
V[u] = top++;
// 将边 <v, u> 与顶点 v 关联
E[top].v = u;
E[top].w = w;
E[top].next = V[v];
V[v] = top++;
int main()
return 0 ;
在上述代码中。
V[MX] :用于存储顶点;
E[MX] : 用于存储边,与边相连的顶点、权重,与顶点相连的下一个边;
top : 记录的是边的数量;
「邻接表」的存储每个顶点就像一个链表,从顶点出发可以查找到与该顶点相连的所有边以及边上的顶点,不相关的顶点不会出现在这个链表上。
接下来看一下如何遍历图。
🍅3.2 遍历图
只要通过邻接表存储好图,遍历图就很简单了,下面直接先来看下代码。
#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <algorithm>
using namespace std ;
const int MX = 1000;
int top;
int V[MX];
bool vis[MX];
struct Edge
int v;
int next; //下标和内容均为边序号
E[MX];
// 初始化
void init()
top = 0;
memset(V, -1, sizeof(V));
memset(vis, -1, sizeof(vis));
// 存储无向图
void addAdge(int u, int v)
// 将边 <u, v> 与顶点 u 关联
E[top].v = v;
E[top].next = V[u];
V[u] = top++;
// 将边 <v, u> 与顶点 v 关联
E[top].v = u;
E[top].next = V[v];
V[v] = top++;
// v 是待查找的顶点
bool dfsAdjacencyList(int u, int v)
// 找到顶点 v
if(u == v)
return true;
// 遍历与 u 相关的所有顶点
for(int i = V[u]; i != -1; i = E[i].next)
int x = E[i].v;
vis[x] = true;
if(dfsAdjacencyList(x, v))
return true;
vis[x] = false;
return false;
/*
测试数据
4 4
0 1
0 2
1 2
1 3
其中,0,1,2,3 分别表示顶点 A,B,C,D
*/
int main()
int n, m;
while(cin>>n>>m)
init();
int u, v;
for(int i = 0; i < m; ++i)
cin>>u>>v;
addAdge(u, v);
cout<<dfsAdjacencyList(0, 3)<<endl;
return 0 ;
其中,主要是 dfsAdjacencyList 函数中的 for 循环遍历与顶点 u 直接相连的所有顶点,上述遍历采用的算法是「深度优先搜索」的方式,使用「邻接表」遍历图。
🔶🔶🔶🔶🔶 我是华丽的分割线 🔶🔶🔶🔶🔶
🍓四、优缺点
「邻接矩阵」适用于「稠密图」,因为「邻接矩阵」是通过顶点来开辟的内存,所以图越稠密,邻接矩阵利用率越高;
「邻接表」适用于「稀疏图」,因为「邻接表」主要以边为基础进行存储,所以图稀疏的时候,更适合使用。
PS :「稠密图」和「稀疏图」可以看这篇文章【数据结构和算法】图的概念都在这里了,讲的明明白白。
🔶🔶🔶🔶🔶 我是华丽的分割线 🔶🔶🔶🔶🔶
🍓五、总结
好了,本篇文章主要对「图」的两种最最最常用的存储方式:「邻接矩阵」存储和「邻接表」存储进行了详细的说明,如果大家还有不理解的地方可以在评论区留言。

🎈 感觉有帮助记得「一键三连」支持下哦!有问题可在评论区留言💬,感谢大家的一路支持!🤞猿哥将持续输出「优质文章」回馈大家!🤞🌹🌹🌹🌹🌹🌹🤞

以上是关于数据结构和算法图必学的两种存储方式,看完即懂的主要内容,如果未能解决你的问题,请参考以下文章