)

Posted 2022-02-16 wyy_persist

//2022.1.15日上午11:02阅读笔记

1.卷积神经网络

到目前为止，我们对机器学习和神经网络的全部回顾都指向了这一点:理解卷积神经网络(Convolutional neural networks, cnn)及其在深度学习中的作用。

在传统的前馈神经网络中(就像我们在第10章中学习的那些)，输入层的每个神经元与下一层的每个输出神经元相连——我们称之为全连接(FC)层。然而，在cnn中，我们直到网络的最后一层才使用FC层。因此，我们可以将CNN定义为一种神经网络，它在一个专门的“卷积”层中交换，而不是在网络[10]中的至少一个层中交换“完全连接”层。

一个非线性激活函数，如ReLU，然后应用这些隆起和卷积的过程的输出= >激活持续(连同其他层类型的混合物的宽度和高度来减少输入量和帮助减少过度拟合)直到我们最终到达的网络和应用一个或两个FC层,我们可以获得ourfinal输出分类。

//截止到2022.1.15日上午11:30

//2022.1.15日晚上21：48开始阅读

CNN中的每一层都应用不同的过滤器集，通常是成百上千个，并将结果组合起来，将输出输入到网络中的下一层。在训练过程中，CNN自动学习这些过滤器的值。

CNN可以学到：

1. 从第一层的原始像素数据中检测边缘；
2. 使用这些边缘来检测第二层的形状(例如，“斑点”)；
3. 在网络的最高层，利用这些形状来检测更高级的特征，如面部结构、汽车部件等；

CNN的最后一层使用这些高级特征对图像的内容进行预测。在实践中，cnn给了我们两个关键的好处:局部不变性和组合性。局部不变性的概念允许我们将图像归类为包含特定对象的图像，而不管该对象出现在图像的哪个位置。我们通过使用“池化层”(在本章后面讨论)来获得这种局部不变量，它确定了我们的输入量的区域，对特定的过滤器有高响应。

第二个好处是组合性。每个过滤器由一个由较低级别特性组成的局部补丁组成转化为更高层次的表示，类似于我们如何在之前的函数(f (g(x(h(x)))的输出基础上构建一组数学函数:f (g(x(h(x)))，这种组合允许我们的网络在更深的层次上学习更丰富的特征。例如，我们的网络可以从像素构建边缘，从边缘构建形状，然后从形状构建复杂的对象——所有这些都是在训练过程中自然发生的自动化方式。从低级特征构建高级特征的概念正是cnn在计算机视觉中如此强大的原因。

在本章的其余部分，我们将详细讨论卷积是什么以及它们在深度学习中的作用。然后，我们将继续介绍cnn的构建块:层，以及用于构建自己的cnn的各种类型的层。我们将通过查看常用模式来结束本章，这些模式用于堆叠这些构建块，以创建CNN架构，该架构在不同的图像分类任务集上表现良好。

在回顾了本章之后，我们将(1)对卷积神经网络和构建卷积神经网络的思维过程有一个很好的理解，(2)我们可以用来构建我们自己的网络架构的一些CNN“食谱”。在下一章中，我们将使用这些基本原理和配方来训练我们自己的cnn。

11.1 理解卷积

本节需要解决的问题：

1. 什么是图像卷积；
2. 卷积如何操作；
3. 为什么使用卷积；
4. 在图像中如何使用卷积；
5. 卷积在深度学习中扮演什么角色；

曾经应用模糊或平滑的图像?对，这是一个卷积。那么边缘检测呢?是的,卷积。你是否打开Photoshop或GIMP来锐化图像?你猜对了，卷积。卷积是计算机视觉和图像处理中最关键、最基本的组成部分之一。

在深度学习方面，一个(图像)卷积是两个矩阵的元素级乘法，后面跟着一个和。

卷积：

1. 取两个矩阵(它们的维数相同)；
2. 将它们逐个相乘(也就是说，不是点积，只是简单的乘法)。
3. 把元素求和。

11.1.1 卷积和互相关联

然而，几乎所有的机器学习和深度学习库都使用了简化的互相关函数：

 

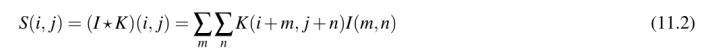
所有这些数学计算都是在我们如何访问图像I的坐标时的符号改变(即，当应用互相关时，我们不需要相对于输入“翻转”内核)。

同样，许多深度学习库使用简化的互相关操作并称之为卷积——我们在这里将使用相同的术语。如果读者有兴趣了解更多关于卷积和互相关背后的数学知识，请参阅Szelski的《计算机视觉:算法和应用》第三章[119]。

11.1.2 “大矩阵”和“小矩阵”的类比

图像是一个多维矩阵。我们的图像有宽度(列数#)和高度(行数#)，就像一个矩阵一样。但与你在小学时使用的传统矩阵不同，图像也有深度——图像中通道的数量。

对于一个标准的RGB图像，我们有一个深度为3 -红、绿、蓝通道分别为一个通道。有了这些知识，我们可以把图像想象成一个大矩阵，而核矩阵或卷积矩阵则是一个用于模糊、锐化、边缘检测和其他处理功能的小矩阵。本质上，这个微小的内核位于大图像的顶部，并从左到右、从上到下进行滑动，在原始图像的每个(x, y)坐标处应用数学运算(即卷积)。

为了获得各种图像处理功能，通常需要手工定义核。事实上，你可能已经熟悉了模糊(平均平滑、高斯平滑、中值平滑等)、边缘检测(Laplacian、Sobel、Scharr、Prewitt等)和锐化——所有这些操作都是手工定义的核的形式，它们是专门为执行特定功能而设计的。

这就提出了一个问题:有没有一种方法可以自动学习这些类型的过滤器?甚至使用这些过滤器来进行图像分类和目标检测?当然有。但在此之前，我们需要对核和卷积有更多的了解。

11.1.3 卷积核

再一次，让我们把图像看作一个大矩阵，而把内核看作一个小矩阵(至少就原始的“大矩阵”图像而言)，如图11.1所示。如图所示，我们正在沿着原始图像从左到右和从上到下滑动内核(红色区域)。在原始图像的每个(x, y)坐标处，我们停下来并检查位于图像内核中心的像素的邻域。然后，我们取像素的这个邻域，将它们与内核卷积，并获得单个输出值。输出值存储在与内核中心相同的(x, y)坐标的输出图像中。

如果这听起来令人困惑，不用担心，我们将在下一节中回顾一个示例。但在我们深入研究一个例子之前，让我们看看内核是什么样子的(图11.3):

 

 

上面我们定义了一个3 × 3的正方形核(猜猜这个核是用来做什么的?)核可以是任意矩形大小的MxN，前提是M和N都是奇数。

大多数应用于深度学习和cnn的核都是N × N个方阵，这使得我们能够利用优化的线性代数库，这些库在方阵上运行效率最高。

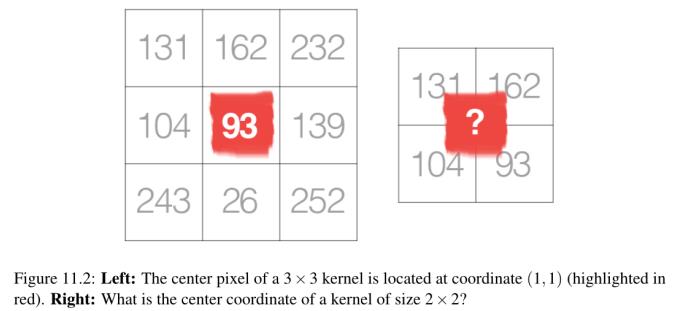
我们使用奇数的内核大小来确保在图像的中心有一个有效的整数坐标(x, y)(图11.2)。在左边，我们有一个3 × 3矩阵。矩阵的中心位于x = 1, y = 1处，其中矩阵的左上角用作原点，我们的坐标为0。但是在右边，我们有一个2 × 2的矩阵。这个矩阵的中心位于x = 0.5, y = 0.5。

但正如我们所知，如果不应用插值，就不存在像素位置(0.5,0.5)这样的东西——我们的像素坐标必须是整数!这正是我们使用奇内核大小的原因:始终确保在内核中心有一个有效的(x, y)坐标。

11.1.4 一个人工计算卷积的例子

卷积需要三个分量:

1. 一个输入的图片；
2. 一个卷积核矩阵，将要用在输入图片上；
3. 一种输出图像，用来存储与核函数卷积的图像的输出；

 

卷积过程：

1. 从原始图像中选择一个(x, y)坐标；
2. 把核的中心放在这个(x, y)坐标上；
3. 取输入图像区域和内核的逐元素乘法，然后将这些乘法操作的值求和为一个值。这些乘法的总和称为内核输出。
4. 使用与步骤1相同的(x, y)坐标，但这一次，将内核输出存储在与输出图像相同的(x, y)位置。

下面你可以找到一个卷积的例子(在数学上表示为?算子)图像的3 × 3区域，带有用于模糊的3 × 3核:

 

在应用这个卷积之后，我们将位于输出图像O的坐标(i, j)的像素设置为Oi, j = 132。

这就是所有的事情!卷积仅仅是核与邻域之间的按元素计算的矩阵乘法的和，该邻域由核覆盖输入图像。

11.1.5 用python实现卷积

 

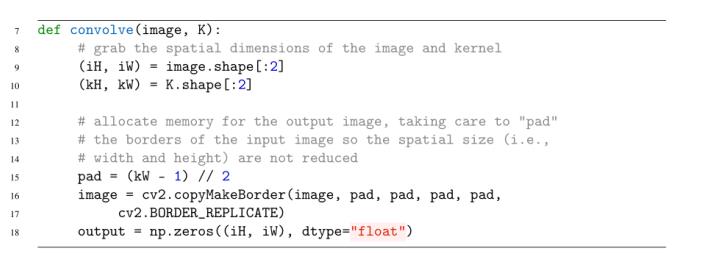
卷积函数需要两个参数:我们想要与核函数卷积的(灰度)图像。给定我们的图像和内核(我们假设它们是NumPy数组)，然后我们确定每个的空间维度(即宽度和高度)(第10行和第11行)。

回想一下，我们的计算是围绕着内核当前所在的输入图像的中心(x, y)坐标“居中”的。这种定位意味着沿着图像边界的像素不存在所谓的“中心”像素(因为内核的角会“悬挂”在图像上，值是未定义的)，如图11.3所示。

空间维数的降低只是对图像应用卷积的一个副作用。有时这种效果是可取的，有时则不然，这完全取决于您的应用程序。

然而，在大多数情况下，我们希望输出图像与输入图像具有相同的尺寸。为了确保尺寸相同，我们应用填充(第15-18行)。在这里，我们只是沿着图像的边界复制像素，这样输出图像将与输入图像的尺寸匹配。

还有其他的填充方法，包括零填充(用零填充边界——这在构建卷积神经网络时很常见)和绕边填充(通过检查图像的对边确定边界像素)。在大多数情况下，您将看到复制或零填充。复制填充通常用于美学方面，而零填充则是提高效率的最佳方法。

现在我们准备将实际的卷积应用到我们的图像上:

 

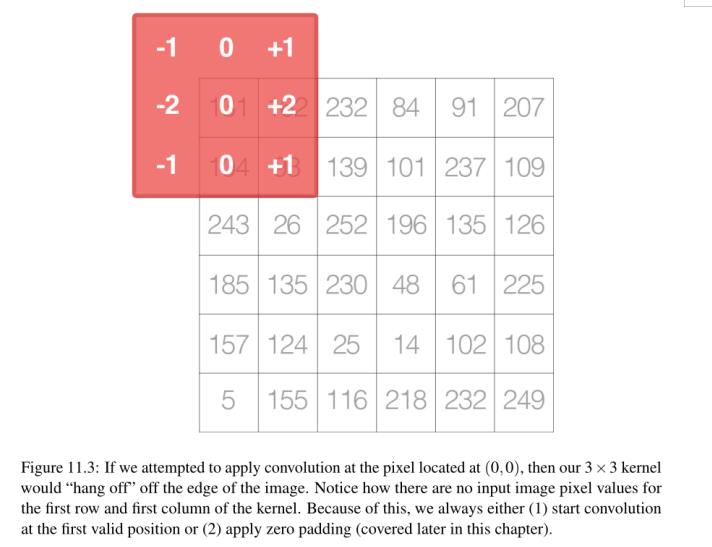
如果我们尝试在位于(0,0)的像素处应用卷积，那么我们的3 × 3核将“挂起”在图像的边缘。注意，内核的第一行和第一列没有输入图像像素值。因此，我们总是(1)在第一个有效的位置开始卷积，或者(2)应用零填充(本章后面会讲到)。

以下为卷积过程：

 

第22和23行在我们的图像上循环，从左到右和从上到下“滑动”内核，每次一个像素。第27行使用NumPy数组切片从图像提取感兴趣区域(Region of Interest, ROI)。roi将以图像的当前(x, y)坐标为中心。roi的大小也将与我们的内核相同，这对下一步至关重要。

卷积在第32行执行，在roi和核之间进行逐元素乘法，然后对矩阵中的项求和。然后存储输出值k在output内存中。

 

当处理图像时，我们通常处理的像素值在[0,255]范围内。然而，当应用卷积时，我们可以很容易地得到超出这个范围的值。为了使输出图像回到范围[0,255]，我们应用scikit-image的rescale_intensity函数(第39行)。

我们还在第40行将图像转换回无符号8位整数数据类型(以前，输出图像是浮点类型，以便处理范围[0,255]之外的像素值)。最后，将输出图像返回给第43行上的调用函数。

既然我们已经定义了卷积函数，让我们继续脚本的驱动程序部分。我们程序的这一部分将处理解析命令行参数，定义一系列我们将应用到我们的图像的内核，然后显示输出结果:

 

然后我们可以定义用于模糊和平滑图像的两个核:

 

为了使你自己相信这个核正在进行模糊处理，注意核中的每一项都是1/S的平均值，其中S是矩阵中的总条目数。因此，该内核将每个输入像素乘以一个小分数并取其和——这正是平均值的定义。

然后我们有一个负责锐化图像的内核:

 

那么用于检测类边缘区域的拉普拉斯核:

 

Sobel核可分别用于检测x轴和y轴上的类边区域:

 

最后，我们定义emboss内核:

 

要了解如何用数学方法构造核并证明其执行给定的图像处理操作，请参考Szeliksi(第3章)[119]。我还推荐使用Setosa的这个优秀的内核可视化工具。io[120]。

考虑到所有这些内核，我们可以将它们合并成一组元组，称为“内核库”:

 

构建这个内核列表可以循环使用它们，并以一种高效的方式可视化它们的输出，如下面的代码块所示:

 

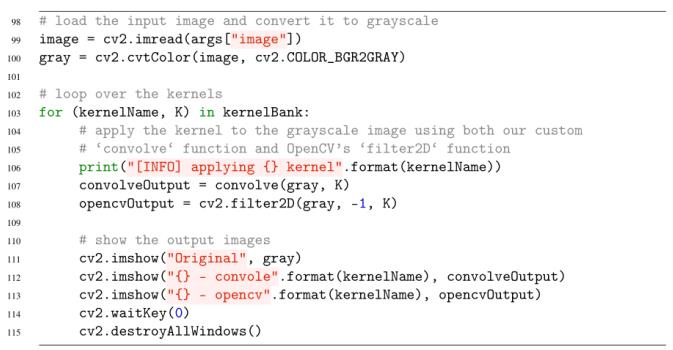
第99和100行从磁盘加载图像并将其转换为灰度。卷积运算符可以应用于RGB或其他多通道体积，但为了简单起见，我们只将我们的过滤器应用于灰度图像。

我们在第103行开始对kernelBank中的核集进行循环，然后通过调用在脚本前面定义的函数convolve方法，将当前内核应用于第104行中的灰度图像。

作为一个完整的检查，我们也调用cv2。filter2D，它也将我们的内核应用到灰度图像。cv2。filter2D函数是OpenCV对卷积函数的优化版本。我在这里包含这两种方法的主要原因是为了检查我们的自定义实现。

最后，第111-115行在屏幕上显示每种内核类型的输出图像。

卷积结果

运行以下命令：

 

然后，您将看到将smallBlur内核应用到输入映像的结果，如图11.4所示。左边是原始图像。然后，在中心，我们得到了卷积函数的结果。右边是来自cv2.filter2D的结果。快速的视觉检查将发现我们的输出与cv2匹配。，表示我们的卷积函数工作正常。此外，我们的图像现在看起来“模糊”和“平滑”，这多亏了平滑核。

让我们应用一个更大的模糊，结果可以在图11.5(左上角)中看到。这次我省略了cv2。filter2D结果以节省空间。比较图11.5和图11.4的结果，注意随着平均内核大小的增加，输出图像中的模糊程度也会增加。

我们还可以锐化我们的图像(图11.5，上-中)，并通过拉普拉斯算子(上-右)检测边缘类区域。

 

左图:原始输入图像。中心:使用我们的自定义卷积函数应用7 × 7的平均模糊。右:使用OpenCV的cv2应用相同的7 × 7模糊。filter2D—注意这两个函数的输出是如何相同的，这意味着我们的卷积方法得到了正确的实现。

SobelX内核用于查找图像中的垂直边(图11.5，左下)，而sobelely内核则显示水平边(从下到中)。最后，我们可以在左下角看到浮雕内核的结果。

 

左上角:应用21 × 21的平均模糊。请注意，这个图像比图11.4中的更加模糊。中上:使用锐化内核来增强细节。右上:通过拉普拉斯算子检测类边操作。左下:使用Sobel-X内核计算垂直边。从下到中:使用Sobel-Y内核寻找水平边。右下角:应用一个浮雕内核。

11.1.6 卷积在深度学习中的作用

通过应用卷积过滤器、非线性激活函数、池化和反向传播，cnn能够学习能够检测网络底层边缘和斑点状结构的过滤器——然后使用边缘和结构作为“构建块”，最终检测高级对象(例如，人脸、猫、狗、杯子、等等)在网络的更深层。

使用低级别的层来学习高级的特性的过程正是我们前面提到的cnn的组合性。但cnn究竟是如何做到这一点的呢?答案是有目的地堆叠特定的层。在下一节中，我们将讨论这些类型的层，然后检查在许多图像分类任务中广泛使用的常见层叠加模式。

11.2 CNN的构建块

//截止到2022.1.15日晚上23：55

//2022.1.16日上午11:47开始阅读

正如我们在第10章中所学到的，神经网络接受一个输入图像/特征向量(每个条目一个输入节点)，并通过一系列隐藏层对其进行转换，通常使用非线性激活函数。每个隐藏层也由一组神经元组成，其中每个神经元与前一层的所有神经元完全连接。神经网络的最后一层(即“输出层”)也是完全连接的，代表了网络的最终输出分类。正如我们在第10章中所学到的，神经网络接受一个输入图像/特征向量(每个条目一个输入节点)，并通过一系列隐藏层对其进行转换，通常使用非线性激活函数。每个隐藏层也由一组神经元组成，其中每个神经元与前一层的所有神经元完全连接。神经网络的最后一层(即“输出层”)也是完全连接的，代表了网络的最终输出分类。

然而，正如第10.1.4节的结果所示，神经网络直接在原始像素强度上运行:

1. 当图像大小增加时，不能很好地缩放；
2. 还有很多精确度有待提高(例如，CIFAR-10上的标准前馈注册网络只有15%的精确度)。

为了说明标准神经网络在图像大小增加时如何不能很好地扩展，让我们再次考虑CIFAR-10数据集。CIFAR-10中的每幅图像都是32 × 32，带有红、绿、蓝通道，向我们的网络输出的总输入量为32 × 32 × 3 = 3,072；

总共072输入似乎并没有什么了不起,但想想如果我们使用250×250像素的图像-输入和权值的总数将跃升至250×250×3 = 187,500,这个数字仅为输入层单独!当然，我们想要添加多个隐藏层，每个层的节点数量都不同——这些参数可以快速叠加，并且考虑到标准神经网络在原始像素强度上的糟糕性能，这种膨胀是不值得的。

相反，我们可以使用利用输入的卷积神经网络(Convolutional Neural Networks, cnn)图像结构，并以更合理的方式定义网络架构。与标准的神经网络不同，CNN的各层以三维方式排列在一个三维体中:宽度、高度和深度(其中深度指的是体积的第三维，如图像中的通道数量或一层中的过滤器数量)。

为了使这个示例更具体，再次考虑CIFAR-10数据集:输入体积的尺寸为32 × 32 × 3(分别为宽度、高度和深度)。后续各层的神经元只会连接到前一层的一小块区域(而不是标准神经网络的全连接结构)——我们称之为局部连接，它使我们能够在网络中保存大量参数。最后，输出层将是一个1 × 1 × N的体积，表示图像提炼成一个单一的类别分数向量。以CIFAR-10为例，给定10类，N = 10，产生1 × 1 × 10体积。

11.2.1 层类型

最可能遇到的层：

1. 卷积层；
2. 激活层；
3. Pooling层；
4. 全连接层（FC）层；
5. 批量正则化；
6. Dropout（DO）层；

以特定的方式叠加一系列的这些层会生成CNN。我们经常使用简单的文本图来描述CNN: INPUT => CONV => RELU => FC => SOFTMAX。

在这里，我们定义了一个简单的CNN，它接受一个输入，应用一个卷积层，然后是一个激活层，然后是一个全连接层，最后是一个softmax分类器来获得输出分类概率。SOFTMAX激活层通常在网络图中被忽略，因为它被认为直接遵循最终的FC。

在这些层类型中，CONV和FC(在较小程度上，BN)是唯一包含在训练过程中学习的参数的层。激活和退出层本身并不被认为是真正的“层”，但是经常包含在网络图中以使体系结构显式地清晰。与CONV和FC同等重要的池化层(POOL)也包含在网络图中，因为当图像在CNN中移动时，池化层对图像的空间维度有重大影响。

CONV、POOL、RELU和FC在定义实际网络架构时是最重要的。这并不是说其他层不重要，而是说在定义实际的体系结构本身时，这四个层是最重要的。

激活函数本身实际上被假定为架构的一部分，当定义CNN架构时，我们经常从表格/图表中忽略激活层以节省空间;然而，激活层被隐式地假定为体系结构的一部分。

在本节的其余部分中，我们将详细回顾这些层类型，并讨论与每个层相关的参数(以及如何设置它们)。在本章的后面，我将更详细地讨论如何正确地堆叠这些层来构建您自己的CNN架构。

11.2.2 卷积层

CONV层是卷积神经网络的核心构件。CONV层参数由一组K个可学习滤波器(即“核”)组成，其中每个滤波器都有宽度和高度，而且几乎总是正方形的。这些滤镜很小(就其空间尺寸而言)，但延伸到整个体量的整个深度。

卷积过程：

 

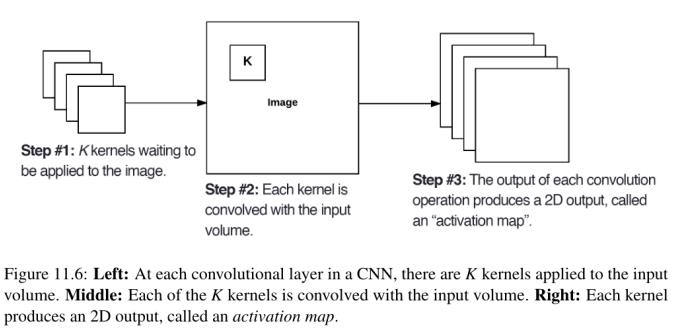
左:在CNN的每一个卷积层，都有K个kernel应用到输入的volume上。中:每一个K核与输入体积卷积。右:每个内核产生一个2D输出，称为激活映射。

 

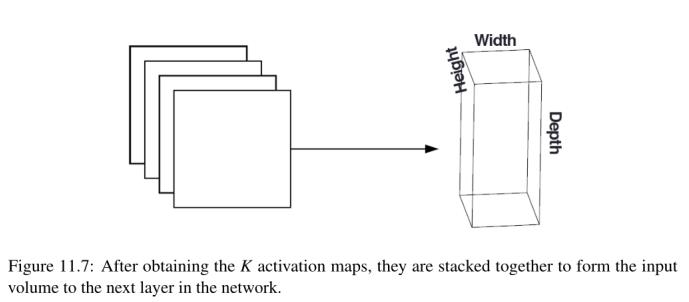
在获得K激活图后，将它们堆叠在一起，形成网络中到下一层的输入量。

因此，输出体积中的每一项都是一个神经元的输出，它只“观察”输入的一个小区域。通过这种方式，网络“学习”了过滤器，当它们在输入量中给定的空间位置看到特定类型的特征时，就会激活过滤器。在网络的较低层，当他们看到边缘或角状区域时，过滤器可能会被激活。

然后，在网络的更深层次，过滤器可能会在高级特征出现时激活，比如脸部的某些部分、狗的爪子、汽车的引擎盖等。这个激活的概念回到我们在第10章中的神经网络类比——当这些神经元看到输入图像中的特定模式时，它们会变得“兴奋”和“活跃”。

在卷积神经网络中，将小滤波器与大(r)输入体积卷积的概念具有特殊意义——具体来说，是神经元的局部连接性和接收域。在处理图像时，将当前卷中的神经元连接到前一卷中的所有神经元通常是不切实际的——因为有太多的连接和太多的权值，使得在具有大空间维度的图像上训练深层网络是不可能的。相反，当使用cnn时，我们选择将每个神经元只连接到输入体积的一个局部区域——我们称这个局部区域的大小为神经元的接受域(或简单地说，变量F)。

为了明确这一点，让我们回到我们的CIFAR-10数据集，其中输入体积为32 × 32 × 3。因此，每个图像的宽度为32像素，高度为32像素，深度为3(每个RGB通道为1)。如果我们receptivefield大小3×3,然后CONV层中的每个神经元将连接到一个3×3图像的局部区域总共3×3×3 = 27权重(记住,thefilters的深度是三个,因为他们通过完整的输入图像的深度扩展,在这种情况下,三个通道)。

现在，让我们假设我们的输入体积的空间维度已经减小到更小的尺寸，但是我们的深度现在变大了，这是因为在网络中使用了更多的过滤器，这样体积大小现在是16 × 16 × 94。同样，如果我们假设一个大小为3 × 3的接收域，那么CONV层中的每个神经元将有3 × 3 × 94 = 846个连接到输入体积。简单地说，接受域F是滤波器的大小，产生一个与输入体积卷积的F × F核。

深度

输出音量的深度控制CONV层中连接到输入音量局部区域的神经元(即滤波器)的数量。每个滤镜生成一个激活图，在有方向的边缘、斑点或颜色出现时激活。

对于给定的CONV层，激活图的深度将是K，或者简单地说，我们在当前层中学习的过滤器的数量。“查看”输入相同(x, y)位置的set过滤器称为depth列。

步长

在上面关于卷积的第11.1.5节中，我们只在每个顶部采取一个像素的步骤。在cnn环境中，同样的原理也可以应用——对于每一步，我们围绕图像的局部区域创建一个新的深度列，在该区域中，我们将每个k过滤器与该区域进行卷积，并将输出存储在一个3D体中。当创建CONV层时，我们通常使用S = 1或S = 2的步幅。

更小的跨步将导致接收域重叠和更大的输出量。相反，更大的跨距将导致接收域重叠更少，输出量更小。为了使卷积大步的概念更具体，考虑表11.1，其中我们有一个5 × 5的输入图像(左)和一个3 × 3的拉普拉斯核(右)。

使用S = 1，我们的内核从左到右、从上到下滑动，一次一个像素，产生以下输出(图11.2，左)。但是，如果我们要应用相同的操作，只有这次的步幅为S = 2，我们一次跳过两个像素(x轴两个像素，y轴两个像素)，产生较小的输出量(右图)。

 

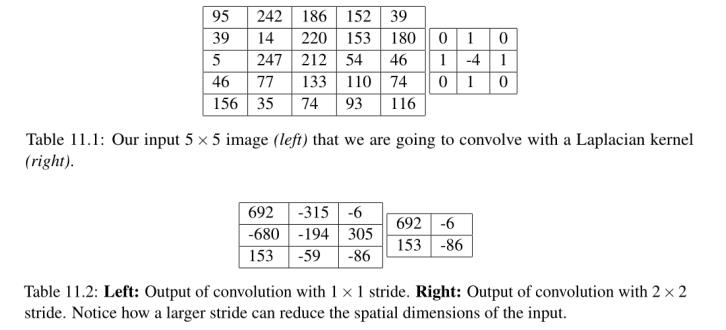
因此，我们可以看到卷积层是如何通过改变内核的步幅来减少输入体积的空间维度的。正如我们将在本节后面看到的，卷积层和池化层是减少空间输入大小的主要方法。池层部分还将提供一个更直观的示例，说明不同的stride大小将如何影响输出大小。

0填充

正如我们在第11.1.5节中所知道的，当应用卷积时，我们需要“填充”图像的边界以保留原始图像的大小——对于CNN内部的过滤器也是如此。使用零填充，我们可以沿着边界“填充”我们的输入，这样我们的输出体积大小匹配我们的输入体积大小。我们应用的填充量由参数P控制。

当我们开始研究将多个卷积滤波器相互叠加在一起的深层CNN架构时，这种技术尤为关键。为了可视化零填充，请再次参考表11.1，在其中，我们将3 × 3的拉普拉斯核应用于一个跨距为S = 1的5 × 5输入图像。

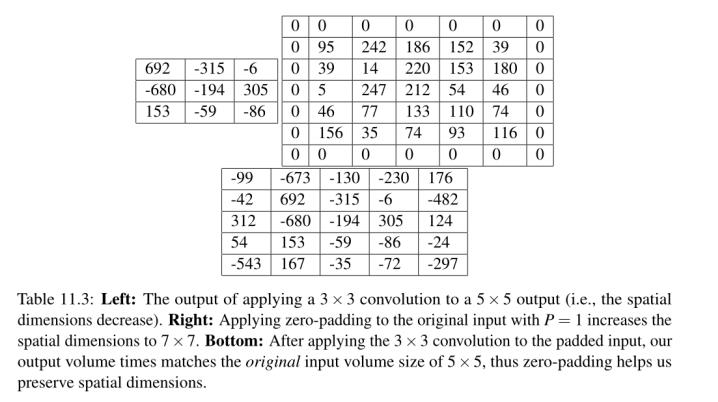
从表11.3(左)可以看出，由于卷积运算的性质，输出体积(3 × 3)小于输入体积(5 × 5)。如果我们设置P = 1，我们可以用0(中间)填充我们的输入体积，以创建一个7 × 7的体积，然后应用卷积运算，导致输出体积大小匹配原始输入体积大小为5 × 5(右边)。

如果没有零填充，输入体积的空间维度会下降得太快，我们将无法训练深层网络(因为输入体积太小，无法从中学习任何有用的模式)。

一起把所有这些参数,我们可以计算出一个输出音量的大小作为输入音量大小的函数(W,假设输入的图像是广场,他们几乎总是),F receptivefield大小,跨步年代和补零p .构建一个有效的CONV层,我们需要确保下面的方程是一个整数:

如果它不是一个整数，那么stride设置不正确，神经元不能平铺，这样它们就不能以对称的方式适应输入体积。

 

以AlexNet架构的第一层为例，它赢得了2012年ImageNet分类挑战，是当前深度学习应用于图像分类热潮的主要原因。在他们的论文中，Krizhevsky等人[94]根据图11.8记录了他们的CNN架构。

 

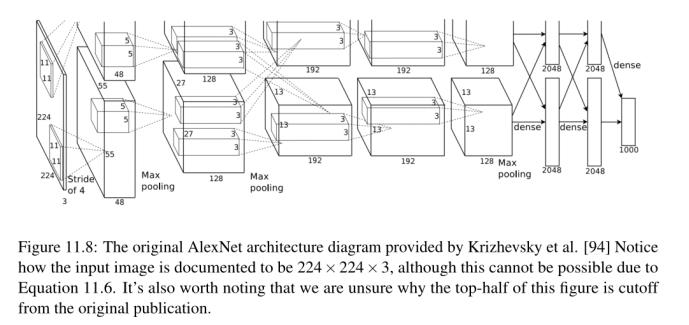
注意，第一层声称输入图像的大小是224 × 224像素。然而，如果我们使用11 × 11的过滤器，步幅为4，并且没有填充，那么这就不可能是正确的:

但是这可能是这篇论文中的一个小错误。

这样的错误比您想象的更常见，因此在通过出版物实现cnn时，一定要自己检查参数，而不是简单地假设列出的参数是正确的。由于CNN中有大量的参数，在编写架构文档时很容易犯排版错误(我自己就做过很多次)。

CONV卷积层：

1. 接受大小为Winput × Hinput × Dinput的输入体积(输入大小通常是方形的，所以通常会看到Winput = Hinput)。
2. 需要四个参数：数字过滤K(它控制输出音量的深度)；接受域大小F(用于卷积的K个核的大小几乎总是平方的，产生一个F × F核)；步长stride S；0填充量；
3. CONV层的输出为Wout put × Hout put × Dout put，其中:

 

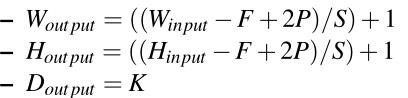
11.2.3 激活层

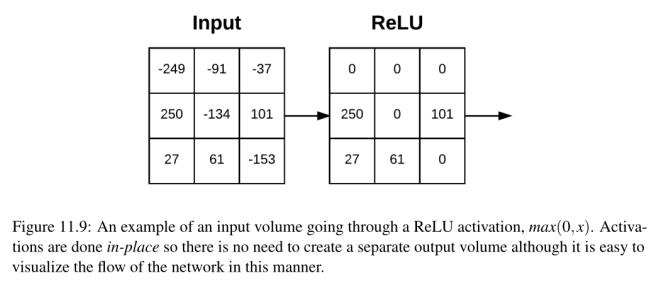
在CNN的每个CONV层之后，我们应用一个非线性激活函数，例如ReLU, ELU，或任何其他在第10章中提到的Leaky ReLU变体。在网络图中，我们通常将激活层表示为RELU，因为RELU激活是最常用的，我们也可以简单地状态为ACT——在任何一种情况下，我们都清楚地表明在网络架构中应用了一个激活函数。

从技术上讲，激活层并不是“层”(由于在激活层中没有学习参数/权值的事实)，有时会从网络架构图中省略，因为它假设一个激活紧跟在卷积之后。

在这种情况下，出版物的作者将在论文的某个地方提到在每个CONV层之后他们正在使用哪个激活函数。以如下组网结构为例:INPUT => CONV => RELU => FC。

为了使这个图更简洁，我们可以简单地删除RELU组件，因为它假设一个激活总是遵循一个卷积:INPUT => CONV => FC。我个人并不喜欢这样，而是选择在网络图中明确包含激活层，以明确我在网络中应用什么时候以及什么激活功能。

激活层接受大小为Winput × Hinput × Dinput的输入量，然后应用给定的激活函数(图11.9)。由于激活函数是按元素的方式应用的，激活层的输出总是与输入维相同，Winput = Wout put, Hinput = Hout put, Dinput = Dout put。

11.2.4 Pooling层

有两种方法可以减小输入量的大小——带stride > 1的CONV层(我们已经看到了)和POOL层。在连续的CONV卷积层之间插入POOL层是很常见的。

 

带有Pooling层的网络架构：

INPUT => CONV => RELU => POOL => CONV => RELU => POOL => FC

POOL层的主要功能是逐步减小输入体积的空间大小(即宽度和高度)。这样做可以减少网络中的参数量和计算量，池也可以帮助我们控制过拟合。

POOL层使用max或average函数分别对输入的每个深度切片进行操作。最大池化通常在CNN架构的中间完成，以减少空间大小，而平均池化通常被用作网络的最后一层(例如，GoogLeNet, SqueezeNet, ResNet)，我们希望完全避免使用FC层。POOL层最常见的类型是max pooling，尽管这种趋势正在随着更多奇异的微架构的引入而改变。

通常我们将使用2 × 2的池大小，尽管使用更大的输入图像(> 200像素)的深层cnn可能在网络架构的早期使用3 × 3的池大小。我们通常也将步幅设置为S = 1或S = 2。图11.10(深受Karpathy等人的启发[121])是一个使用2 × 2池大小和跨度S = 1的最大池化示例。注意，对于每2 × 2块，我们只保留最大的值，采取单一步骤(如滑动窗口)，并再次应用操作-从而产生3 × 3的输出体积大小。

我们可以通过增加步幅来进一步减小输出量的大小——在这里，我们对相同的输入应用S = 2(图11.10，底部)。对于输入的每2 × 2块，我们只保留最大的值，然后取2个像素步，再次进行操作。这个池允许我们将宽度和高度减少2倍，有效地丢弃了前一层75%的激活。

总而言之，POOL层接受大小为Winput × Hinput × Dinput的输入量。然后它们需要两个参数:

1. 接受域大小F(也称为“池大小”)；
2. 步长stride S；

应用POOL操作得到一个大小为Wout put × Hout put × Dout put的输出量，其中:

 

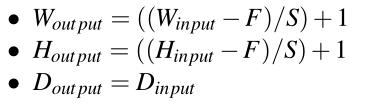
两种不同的Max pooling方法：

1. F = 3, S = 2，称为重叠池，通常应用于具有较大空间维度的图像/输入体；
2. F = 2 ，S = 2这叫做非重叠池。这是最常见的池化类型，适用于空间维度较小的图像。对于接受较小输入图像(在32 - 64像素范围内)的网络架构，您可能还会看到F = 2, S = 1。

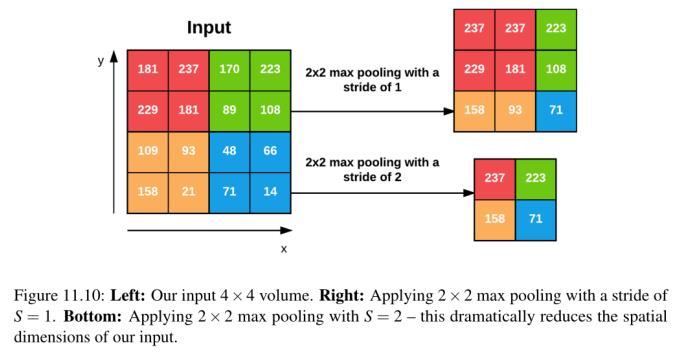
左:我们的输入4 × 4体积。右图:在S = 1的步幅上应用2 × 2的最大池化。底部:应用2 × 2 max pooling (S = 2)——这极大地减少了我们输入的空间维度。

对于接受较小输入图像(在32 - 64像素范围内)的网络架构，您可能还会看到F = 2, S = 1。

使用CONV卷积还是Pooling层？

Springenberg等人在2014年的论文《力求简单:The All Convolutional Net》[122]中建议完全抛弃POOL层，而简单地依赖步幅较大的CONV层来处理volume的空间维度的下采样。他们的工作表明，这种方法在各种数据集上都能很好地工作，包括CIFAR-10(小图像，低数量的类)和ImageNet(大输入图像，1000个类)。ResNet架构[96]延续了这一趋势，该架构也使用CONV层进行下采样。

11.2.5 全连接层

FC层中的神经元完全连接到前一层中的所有激活，正如我们在第10章中讨论的前馈神经网络的标准一样。FC层总是放置在网络的末端(即，我们不应用一个CONV层，然后一个FC层，然后是另一个CONV)层。

在应用softmax分类器之前，通常会使用一个或两个FC层，如下(简化)架构所示:

 

在这里，我们在(隐含的)softmax分类器之前应用两个完全连接的层，该分类器将计算每个类的最终输出概率。

11.2.6 批量正则化

首次引入约飞和Szgedy在他们一份2015年的论文,批量标准化:加速深层网络训练通过减少内部协变量[123]转变,一批标准化层(简称BN),顾名思义,是用来规范给定输入的激活体积在网络中传递到下一层。

如果我们认为x是我们的小批量激活，那么我们可以通过以下公式计算标准化的ˆx:

 

在训练过程中，我们计算每个小批量β的µβ和σβ，其中:

 

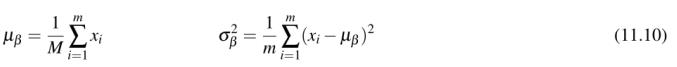
我们设置ε等于一个小的正值，例如1e-7，以避免取零的平方根。应用这个方程意味着，离开批处理规范化层的激活将具有大约为零的平均值和单位方差(即，以零为中心)。

在测试时，我们用训练过程中计算的µ- β和σ - β的运行平均值来代替小批量的µ- β和σ - β。这确保了我们可以通过我们的网络来传递图像，并且仍然可以获得准确的预测，而不会受到训练时通过网络的最终小批量图像的µβ和σβ的影响。

批处理归一化已经被证明在减少训练神经网络所需的时间方面是非常有效的。批处理标准化还具有帮助“稳定”训练的额外好处，允许更大的学习速率和正则化强度。当然，使用批处理规范化并不会减少对这些参数的调优需求，但它会使学习速率和正则化的波动更小，调优更简单，从而使您的工作更轻松。当您在网络中使用批处理规范化时，您还会注意到较低的最终损耗和更稳定的损耗曲线。

批处理标准化的最大缺点是，由于每批统计数据和标准化的计算，它实际上会将训练网络所需的时间(尽管您需要更少的时间来获得合理的准确性)降低2-3倍。

也就是说，我建议在几乎所有情况下都使用批处理规范化，因为它确实会产生显著的差异。正如我们在本书后面会看到的，将批处理归一化应用到我们的网络架构中可以帮助我们防止过拟合，并允许我们在更少的时间内获得显著更高的分类精度，相比之下，相同的网络架构没有批处理归一化。

批处理正则化层放在那？

您可能已经注意到，在我对批处理规范化的讨论中，我遗漏了在网络体系结构中放置批处理规范化层的确切位置。根据Ioffe和Szegedy的原始论文[123]，他们将批归一化(BN)置于激活之前:

我们通过将x = Wu + b归一化，在非线性之前加上BN变换。

使用这个方案，一个利用批处理标准化的网络架构看起来像这样:

 

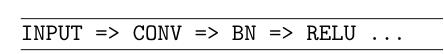
然而，这种批处理规范化的观点从统计的角度来看是没有意义的。在这种情况下，BN层归一化来自CONV层的特征分布。其中一些特征可能是负面的，在这种情况下，它们将被非线性激活函数(如ReLU)箝位(即设置为零)。

如果我们在激活之前进行标准化，我们本质上是在标准化中包含负值。我们的零中心特性然后