OpenCV 完整例程72. 一维离散傅里叶变换

Posted 小白YouCans

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了OpenCV 完整例程72. 一维离散傅里叶变换相关的知识，希望对你有一定的参考价值。

【OpenCV 完整例程】72. 一维离散傅里叶变换

欢迎关注 『OpenCV 完整例程 100 篇』 系列，持续更新中
欢迎关注 『Python小白的OpenCV学习课』 系列，持续更新中

1.3 一维离散傅里叶变换

数字信号和数字图像都是采样得到的离散变量。

对原函数的变换取样后的数据

F ~ ( μ ) = ∫ − ∞ + ∞ f ~ ( t ) e − j 2 π μ t d t = ∫ − ∞ + ∞ ∑ n = − ∞ ∞ f ( t ) δ ( t − n Δ T ) e − j 2 π μ t d t = ∑ n = − ∞ ∞ ∫ − ∞ + ∞ f ( t ) δ ( t − n Δ T ) e − j 2 π μ t d t = ∑ n = − ∞ ∞ f n e − j 2 π μ n Δ T \\beginaligned \\tildeF(\\mu) &= \\int_-\\infty^+\\infty \\tildef(t) e^-j 2 \\pi \\mu t dt\\\\ &= \\int_-\\infty^+\\infty \\sum_n=-\\infty^\\infty f(t) \\delta (t-n\\Delta T) e^-j 2 \\pi \\mu t dt\\\\ &= \\sum_n=-\\infty^\\infty \\int_-\\infty^+\\infty f(t) \\delta (t-n\\Delta T) e^-j 2 \\pi \\mu t dt\\\\ &= \\sum_n=-\\infty^\\infty f_n e^-j 2 \\pi \\mu n\\Delta T\\\\ \\endaligned F~(μ)​=∫−∞+∞​f~​(t)e−j2πμtdt=∫−∞+∞​n=−∞∑∞​f(t)δ(t−nΔT)e−j2πμtdt=n=−∞∑∞​∫−∞+∞​f(t)δ(t−nΔT)e−j2πμtdt=n=−∞∑∞​fn​e−j2πμnΔT​

当取样频率为 μ = m / M Δ T \\mu = m/M \\Delta T μ=m/MΔT 时，可以得到离散傅里叶变换（DFT）和逆变换公式为：

F m = ∑ n = 0 M − 1 f n e − j   2 π μ m n / M , m = 0 , . . . M − 1 f n = 1 M ∑ m = 0 M − 1 F m e j   2 π μ m n / M , n = 0 , . . . M − 1 \\beginaligned F_m &= \\sum_n=0^M-1 f_n e^-j\\ 2\\pi \\mu mn/M, &m=0,...M-1\\\\ f_n &= \\frac1M \\sum_m=0^M-1 F_m e^j\\ 2\\pi \\mu mn/M, &n=0,...M-1 \\endaligned Fm​fn​​=n=0∑M−1​fn​e−j 2πμmn/M,=M1​m=0∑M−1​Fm​ej 2πμmn/M,​m=0,...M−1n=0,...M−1​

由于任何周期或非周期函数都可以表示为不同频率的正弦函数和余弦函数之和的形式，因此用傅里叶变换表示的函数特征完全可以通过傅里叶反变换来重建，而且不会丢失任何信息。这是频率域图像处理的数学基础。

离散傅里叶变换 是将离散信号分解为一系列离散三角函数分量，每个三角函数分量都有对应的幅值 A、频率 f 和相位 φ \\varphi φ。通过所有分量叠加可以得到原离散信号。

在图像处理中，通常使用 x , y x, y x,y 表示离散的空间域坐标变量，用 u , v u,v u,v 表示离散的频率域变量。于是将一维离散傅里叶变换表示为：

F ( u ) = ∑ x = 0 M − 1 f ( x ) e − j   2 π u x / M , u = 0 , . . . M − 1 f ( x ) = 1 M ∑ u = 0 M − 1 F ( u ) e j   2 π u x / M , x = 0 , . . . M − 1 \\beginaligned F(u) &= \\sum_x=0^M-1 f(x) e^-j\\ 2\\pi u x/M, &u=0,...M-1\\\\ f(x) &= \\frac1M \\sum_u=0^M-1 F(u) e^j\\ 2\\pi u x/M, &x=0,...M-1 \\endaligned F(u)f(x)​=x=0∑M−1​f(x)e−j 2πux/M,=M1​u=0∑M−1​F(u)ej 2πux/M,​u=0,...M−1x=0,...M−1​


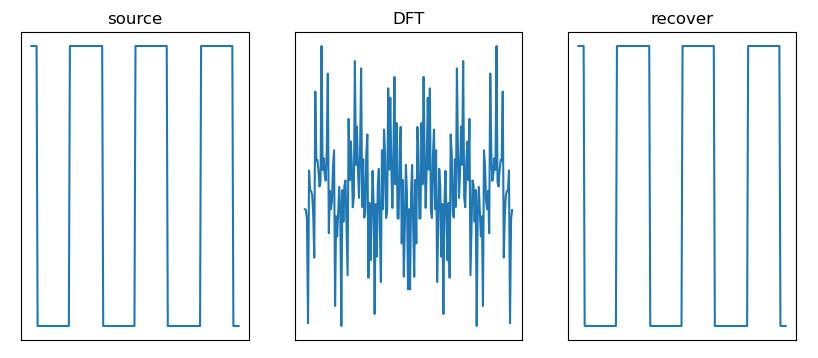
例程 8.6：一维离散傅里叶变换

    # 8.6：一维离散傅里叶变换
    # 生成方波信号
    N = 200
    t = np.linspace(-10, 10, N)
    dt = t[1] - t[0]
    sint = np.sin(t)
    sig = np.sign(sint)
    fig = plt.figure(figsize=(10, 4))
    plt.subplot(131), plt.title("source"), plt.xticks([]), plt.yticks([])
    plt.plot(t, sig)

    # 离散傅里叶变换
    fft = np.fft.fft(sig, N)  # 离散傅里叶变换
    fftshift = np.fft.fftshift(fft)  # 对称平移
    amp = abs(fftshift) / len(fft)  # 幅值
    pha = np.angle(fftshift)  # 相位
    fre = np.fft.fftshift(np.fft.fftfreq(d=dt, n=N))  # 频率
    plt.subplot(132), plt.title("DFT"), plt.xticks([]), plt.yticks([])
    plt.plot(t, fft)

    # 信号恢复
    recover = np.zeros(N)
    for a, p, f in zip(amp, pha, fre):
        sigCos = a * np.cos(2 * np.pi * f * np.arange(N) * dt + p)  # 根据幅度,相位,频率构造三角函数
        recover += sigCos  # 把这些三角函数都加起来

    plt.subplot(133), plt.title("recover"), plt.xticks([]), plt.yticks([])
    plt.plot(t, recover)
    plt.show()


（本节完）

版权声明：

youcans@xupt 原创作品，转载必须标注原文链接

Copyright 2021 youcans, XUPT

Crated：2022-1-15


欢迎关注 『OpenCV 完整例程 100 篇』 系列，持续更新中
欢迎关注 『Python

以上是关于OpenCV 完整例程72. 一维离散傅里叶变换的主要内容，如果未能解决你的问题，请参考以下文章

OpenCV 完整例程75. Numpy 实现图像傅里叶变换

OpenCV 完整例程76. OpenCV 实现图像傅里叶变换

OpenCV 完整例程77. OpenCV 实现快速傅里叶变换

OpenCV 完整例程73. 二维连续傅里叶变换

OpenCV C++（十）----傅里叶变换

opencv学习笔记第七篇：离散傅里叶变换