第十一届蓝桥杯省赛B组做题记录(python)

Posted 2022-02-06 z.volcano

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了第十一届蓝桥杯省赛B组做题记录(python)相关的知识，希望对你有一定的参考价值。

蓝桥杯

结果填空
程序设计

结果填空

门牌制作

问题描述
小蓝要为一条街的住户制作门牌号。

这条街一共有 2020 位住户，门牌号从 1 到 2020 编号。

小蓝制作门牌的方法是先制作 0 到 9 这几个数字字符，最后根据需要将字符粘贴到门牌上，

例如门牌 1017 需要依次粘贴字符 1、0、1、7，即需要 1 个字符 0，2 个字符 1，1 个字符 7。

请问要制作所有的 1 到 2020 号门牌，总共需要多少个字符 2？

答案提交
这是一道结果填空的题，你只需要算出结果后提交即可。
本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

n=0
for i in range(1,2021):
    n += str(i).count('2')
print(n)
#624

既约分数

问题描述
如果一个分数的分子和分母的最大公约数是 1，这个分数称为既约分数。

请问，有多少个既约分数，分子和分母都是 1 到 2020 之间的整数（包括 1 和 2020）？

答案提交
这是一道结果填空题，你只需要算出结果后提交即可。
本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

def gcd(a,b):
    if b ==0 : return a
    return gcd(b,a%b)

n=2020
for i in range(1,2021):
    for j in range(2,2021):
        if gcd(i,j) == 1:
            n += 1
print(n)
#2481215

蛇形填数

问题描述
如下图所示，小明用从 1 开始的正整数 “蛇形” 填充无限大的矩阵。

容易看出矩阵第二行第二列中的数是 5，请你计算矩阵中第 20 行第 20 列的数是多少？

观察前四个数，1、5、13、25，依次相差4、8、12，按照这个规律

n=1
for i in range(1,20):
    n += i*4
print(n)
#761

跑步锻炼

问题描述
小蓝每天都锻炼身体。

正常情况下，小蓝每天跑 1 千米。

如果某天是周一或者月初（1 日），为了激励自己，小蓝要跑 2 千米。

如果同时是周一或月初，小蓝也是跑 2 千米。

小蓝跑步已经坚持了很长时间，从 2000 年 1 月 1 日周六（含）到 2020 年10 月 1 日周四（含）。

请问这段时间小蓝总共跑步多少千米？

答案提交
这是一道结果填空的题，你只需要算出结果后提交即可。

这里提供一种偷懒的思路，在excel表格中算出总天数7580

接着算出共有1083个周一，250个月初，然后翻日历，发现有34天既是周一又是月初

所以答案：7580+1083+250-34=8879

七段码

题目描述
小蓝要用七段码数码管来表示一种特殊的文字。

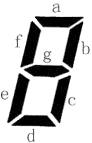
上图给出了七段码数码管的一个图示，数码管中一共有 7 段可以发光的二极管，分别标记为 a, b, c, d, e, f, g。

小蓝要选择一部分二极管（至少要有一个）发光来表达字符。在设计字符的表达时，要求所有发光的二极管是连成一片的。

例如：b 发光，其他二极管不发光可以用来表达一种字符。

例如：c 发光，其他二极管不发光可以用来表达一种字符。

这种方案与上一行的方案可以用来表示不同的字符，尽管看上去比较相似。

例如：a, b, c, d, e 发光，f, g 不发光可以用来表达一种字符。

例如：b, f 发光，其他二极管不发光则不能用来表达一种字符，因为发光的二极管没有连成一片。

请问，小蓝可以用七段码数码管表达多少种不同的字符？

这题也是手动算了一下，答案是7+10+16+20+19+7+1= 80

程序设计

成绩统计

题目描述
小蓝给学生们组织了一场考试，卷面总分为 100 分，每个学生的得分都是一个 0 到 100 的整数。

如果得分至少是 60 分，则称为及格。
如果得分至少为 85 分，则称为优秀。
请计算及格率和优秀率，用百分数表示，百分号前的部分四舍五入保留整数。

输入格式
输入的第一行包含一个整数 n，表示考试人数。
接下来 n 行，每行包含一个 0 至 100 的整数，表示一个学生的得分。

输出格式
输出两行，每行一个百分数，分别表示及格率和优秀率。

百分号前的部分四舍五入保留整数。
输入样例

7
80
92
56
74
88
100
0

输出样例

71%
43%

数据范围

对于 50% 的评测用例，1 ≤ n ≤ 100 1≤n≤1001≤n≤100 对于所有评测用例，1 ≤ n ≤ 10000
1≤n≤100001≤n≤10000

import math

def deal(n):
    if math.modf(n)[0] >= 0.5:
        return int(n)+1
    else:
        return int(n)

sum = 0
you = 0
n=int(input())
for i in range(n):
    x = int(input())
    if x >= 85:
        sum += 1
        you += 1
    elif x >= 60:
        sum += 1
print("%".format(deal(sum/n*100)))
print("%".format(deal(you/n*100)))

回文日期

题目描述
2020 年春节期间，有一个特殊的日期引起了大家的注意：2020 年 2 月 2 日。

因为如果将这个日期按 yyyymmdd 的格式写成一个 8 位数是 20200202，恰好是一个回文数。

我们称这样的日期是回文日期。

有人表示 20200202 是“千年一遇” 的特殊日子。

对此小明很不认同，因为不到 2 年之后就是下一个回文日期：20211202 即 2021 年 12 月 2 日。

也有人表示 20200202 并不仅仅是一个回文日期，还是一个 ABABBABA 型的回文日期。

对此小明也不认同，因为大约 100 年后就能遇到下一个 ABABBABA 型的回文日期：21211212 即 2121 年 12 月 12 日。

算不上“千年一遇”，顶多算“千年两遇”。

给定一个 8 位数的日期，请你计算该日期之后下一个回文日期和下一个 ABABBABA 型的回文日期各是哪一天。

注意：下一个回文日期和下一个 ABABBABA 型的回文日期可能是同一天。

ABABBABA 型的回文日期，需要满足 A≠B。

输入格式
输入包含一个八位整数 N，表示日期。

输出格式
第一行表示下一个回文日期，
第二行表示下一个 ABABBABA 型的回文日期。

输入样例

20200202

输出样例

20211202 21211212

数据范围
对于所有评测用例，10000101 ≤ N ≤ 89991231，保证 N 是一个合法日期的 8 位数表示。

感觉不需要，所以没有判断闰年，最后也是通过了所有测试点

s = input()
d = 1:31,2:28,3:31,4:30,5:31,6:30,7:31,8:31,9:30,10:31,11:30,12:31

def huiwen(s):
    if s[:4] == s[4:][::-1]:
        return 1
    return 0

def ab(s):
    if s[0] == s[2] and s[1] == s[3] and s[0] != s[1]:
        return 1
    return 0

year = int(s[:4])
month = int(s[4:6])
day = int(s[6:])
out = []

while True:
    if month <= 12:
        if day <= d[month]:
            date = str(year).zfill(4)+str(month).zfill(2)+str(day).zfill(2)
            if huiwen(date): 
                out.append(date)
                if ab(date):
                    print(out[0])
                    print(date)
                    break
            day += 1
        else:
            month += 1
            day = 1
    else:
        month = 1
        year += 1

子串分值和

题目描述

输入格式
输入一行包含一个由小写字母组成的字符串 S。

输出格式
输出一个整数表示答案。

输入样例

ababc

输出样例

28

样例解释

子串 f值
a     1
ab    2
aba   2
abab  2
ababc 3
 b    1
 ba   2
 bab  2
 babc 3
  a   1
  ab  2
  abc 3
   b  1
   bc 2
    c 1

数据范围
对于 20% 的评测用例，1 ≤ n ≤ 10 1 ≤ n ≤ 101≤n≤10；
对于 40% 的评测用例，1 ≤ n ≤ 100 1 ≤ n ≤ 1001≤n≤100；
对于 50% 的评测用例，1 ≤ n ≤ 1000 1 ≤ n ≤ 10001≤n≤1000；
对于 60% 的评测用例，1 ≤ n ≤ 10000 1 ≤ n ≤ 100001≤n≤10000；
对于所有评测用例，1 ≤ n ≤ 100000 1 ≤ n ≤ 1000001≤n≤100000。

暴力枚举的话可以拿到40％的分数，想拿100得换个思路。

以字符串ababc为例，包含第二个b的所有子串共有8个，但是后4个才是符合这种思路的子串

#abab  
#ababc 
# bab  
# babc 
  ab  
  abc 
   b  
   bc

由题意可知，字符串中出现过一次b之后，后面再出现b就不参与计数了

所以这里需要统计某个字母当前位置与上一次出现的位置的距离和当前位置到末位位置的距离，这里是2*2=4

遍历求和之后就是答案，即1 *5+2 *4+2 *3+2 *2+4 *1=28

s = input()
#存放每个字母第一次出现的位置
lt = [-1 for i in range(26)]
out = 0

for i in range(len(s)):
    #当前字母的下标,获取上一次出现的位置
    ind = ord(s[i])-97
    
    x = i - lt[ind]
    y = len(s) - i
    out += x*y
    lt[ind] = i
print(out)

平面切分

输出格式
一个整数代表答案。

样例输入

3
1 1
2 2
3 3

样例输出

6

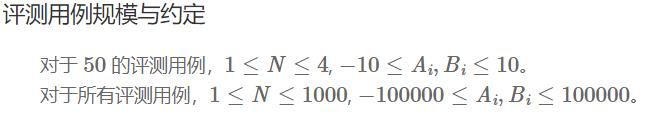
没有直线时，只有一个平面；当有一条直线时，平面被分成两部分，此后每增加一条直线，与已有的直线的位置关系有三种情况：平行、重合、相交。

重合的话不会增加被划分成的部分数。
如果增加的直线与已有的所有直线都平行，则划分出的部分数量+1
如果相交的话，新的直线和已有的直线共有n个交点，则划分出的部分数量多出n+1

所以重点是统计不重合的直线的数量和交点数。

如果两条直线的斜率和截距不完全相同，则为不同直线；接着统计加入新的直线后增加的交点数。

此处代码实现参考了第十一届蓝桥杯软件类Python组（最新）

n = int(input())
line = [] #存放不同直线的斜率和截距
for i in range(n):
    tmp = [int(a) for a in input().split()]
    line.append(tuple(tmp))
line = list(set(line)) #去重
#直线个数
n = len(line)
judge = lambda p1,p2 : abs(p1[0] - p2[0]) + abs(p1[1] - p2[1]) < 1e-12  #判断两个点是否为同一个点
#初始一根直线把平面分为两部分
out = 2

for i in range(1,n): #从第二根直线开始
    k1,b1 = line[i]
    point = set()
    for j in range(i):
        k2,b2 = line[j]
        if k2 == k1: #平行无交点
            continue
        #交点坐标
        x = (b2-b1)/(k1-k2)
        y = k1*x + b1
        point.add((x,y))
    m = len(point)
    ms = m+1
    if m <= 1:
        out += ms
    else:
        point = sorted(list(point),key = lambda x:x[0])
        for li in range(1,m):
            if judge(point[li-1],point[li]):
                ms -= 1
        out += ms
print(out)